我們通常采用MSE、RMSE、MAE、R2來評價回歸預測算法。

1、均方誤差：MSE（Mean Squared Error）

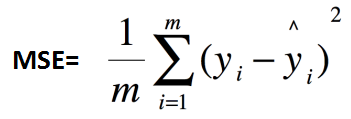
其中，為測試集上真實值-預測值。

def rms(y_test, y):
return sp.mean((y_test - y) ** 2)

?

2、均方根誤差：RMSE（Root Mean Squard Error）

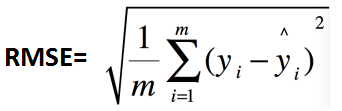
可以看出，RMSE=sqrt（MSE）。

3、平均絕對誤差：MAE（Mean Absolute Error）

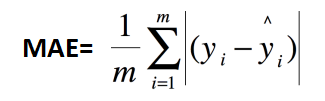
以上各指標，根據不同業務，會有不同的值大小，不具有可讀性，因此還可以使用以下方式進行評測。

4、決定系數：R2（R-Square）

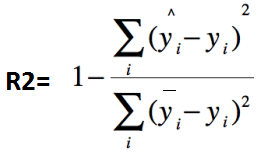
def R2(y_test, y_true):
return 1 - ((y_test - y_true)**2).sum() / ((y_true - y_true.mean())**2).sum()

?

其中，分子部分表示真實值與預測值的平方差之和，類似于均方差 MSE；分母部分表示真實值與均值的平方差之和，類似于方差 Var。

根據?R-Squared 的取值，來判斷模型的好壞，其取值范圍為[0,1]：

如果結果是 0，說明模型擬合效果很差；

如果結果是 1，說明模型無錯誤。

一般來說，R-Squared 越大，表示模型擬合效果越好。R-Squared 反映的是大概有多準，因為，隨著樣本數量的增加，R-Square必然增加，無法真正定量說明準確程度，只能大概定量。

5、校正決定系數（Adjusted R-Square）

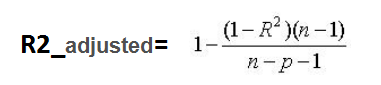
其中，n 是樣本數量，p 是特征數量。

Adjusted R-Square?抵消樣本數量對 R-Square的影響，做到了真正的 0~1，越大越好。

python中可以直接調用

from sklearn.metrics import mean_squared_error #均方誤差from sklearn.metrics import mean_absolute_error #平方絕對誤差from sklearn.metrics import r2_score#R square#調用MSE：mean_squared_error(y_test,y_predict)RMSE:np.sqrt(mean_squared_error(y_test,y_predict))MAE：mean_absolute_error(y_test,y_predict)R2：r2_score(y_test,y_predict)Adjusted_R2：:1-((1-r2_score(y_test,y_predict))*(n-1))/(n-p-1)

?

?

?

方差、協方差、標準差(標準偏差/均方差）、均方誤差、均方根誤差(標準誤差)、均方根值

本文由博主經過查閱網上資料整理總結后編寫，如存在錯誤或不恰當之處請留言以便更正，內容僅供大家參考學習。

---

• 方差（Variance)

? ? ? ?方差用于衡量隨機變量或一組數據的離散程度，方差在在統計描述和概率分布中有不同的定義和計算公式。①概率論中方差用來度量隨機變量和其數學期望（即均值）之間的偏離程度；②統計中的方差(樣本方差)是每個樣本值與全體樣本均值之差的平方值的平均數，代表每個變量與總體均值間的離散程度。

概率論中計算公式

離散型隨機變量的數學期望：?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????? ? ? ? ? ? ? ? ? ? ? ? ? ? ?---------求取期望值

連續型隨機變量的數學期望：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ? ? ? ? ? ? ? ? ? ? ? ? ? ----------求取期望值

其中，pi是變量，xi發生的概率，f(x)是概率密度。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ---------求取方差值

?

統計學中計算公式

?總體方差，也叫做有偏估計，其實就是我們從初高中就學到的那個標準定義的方差：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ?-----------求取總體均值

其中，n表示這組數據個數，x1、x2、x3……xn表示這組數據具體數值。

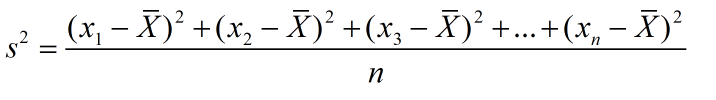? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??------------求取總體方差

其中，為數據的平均數，n為數據的個數，為方差。

樣本方差，無偏方差，在實際情況中，總體均值是很難得到的，往往通過抽樣來計算，于是有樣本方差，計算公式如下

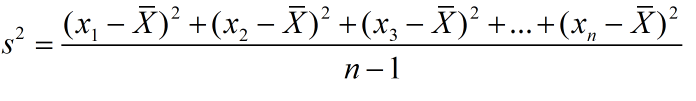? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??--------------求取樣本方差? ? ? ? ? ?

此處，為什么要將分母由n變成n-1，主要是為了實現無偏估計減小誤差，請閱讀《為什么樣本方差的分母是 n-1》。? ??

• 協方差（Covariance）

? ? ??協方差在概率論和統計學中用于衡量兩個變量的總體誤差。而方差是協方差的一種特殊情況，即當兩個變量是相同的情況。協方差表示的是兩個變量的總體的誤差，這與只表示一個變量誤差的方差不同。 如果兩個變量的變化趨勢一致，也就是說如果其中一個大于自身的期望值，另外一個也大于自身的期望值，那么兩個變量之間的協方差就是正值。 如果兩個變量的變化趨勢相反，即其中一個大于自身的期望值，另外一個卻小于自身的期望值，那么兩個變量之間的協方差就是負值。

其中，E[X]與E[Y]分別為兩個實數隨機變量X與Y的數學期望，Cov(X,Y)為X，Y的協方差。

• ?標準差（Standard Deviation)

? ? ? ?標準差也被稱為標準偏差,在中文環境中又常稱均方差，是數據偏離均值的平方和平均后的方根，用σ表示。標準差是方差的算術平方根。標準差能反映一個數據集的離散程度，只是由于方差出現了平方項造成量綱的倍數變化，無法直觀反映出偏離程度，于是出現了標準差，標準偏差越小，這些值偏離平均值就越少，反之亦然。

?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ------------求取樣本標準差

其中，??代表所采用的樣本X1,X2,...,Xn的均值。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?-------------求取總體標準差

?其中，?代表總體X的均值。

例：有一組數字分別是200、50、100、200，求它們的樣本標準偏差。

= (200+50+100+200)/4 = 550/4 = 137.5

= [(200-137.5)^2+(50-137.5)^2+(100-137.5)^2+(200-137.5)^2]/(4-1)

樣本標準偏差 S = Sqrt(S^2)=75

• 均方誤差（mean-square error, MSE）

? ? ? ?均方誤差是反映估計量與被估計量之間差異程度的一種度量，換句話說，參數估計值與參數真值之差的平方的期望值。MSE可以評價數據的變化程度，MSE的值越小，說明預測模型描述實驗數據具有更好的精確度。

• 均方根誤差（root mean squared error，RMSE）

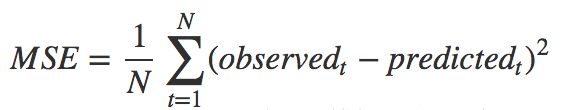
? ? ? 均方根誤差亦稱標準誤差，是均方誤差的算術平方根。換句話說，是觀測值與真值(或模擬值)偏差(而不是觀測值與其平均值之間的偏差)的平方與觀測次數n比值的平方根，在實際測量中，觀測次數n總是有限的，真值只能用最可信賴（最佳）值來代替。標準誤差對一組測量中的特大或特小誤差反映非常敏感，所以，標準誤差能夠很好地反映出測量的精密度。這正是標準誤差在工程測量中廣泛被采用的原因。因此，標準差是用來衡量一組數自身的離散程度，而均方根誤差是用來衡量觀測值同真值之間的偏差。

• 均方根值（root-mean-square，RMES）

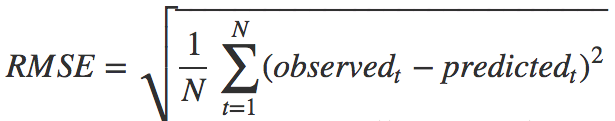
? ? ? ?均方根值也稱作為方均根值或有效值，在數據統計分析中，將所有值平方求和，求其均值，再開平方，就得到均方根值。在物理學中，我們常用均方根值來分析噪聲。

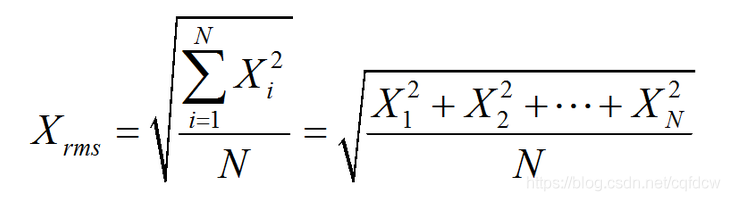
? ? ? ? 比如幅度為100V而占空比為0.5的方波信號，如果按平均值計算，它的電壓只有50V，而按均方根值計算則有70.71V。這是為什么呢？舉一個例子，有一組100伏的電池組，每次供電10分鐘之后停10分鐘，也就是說占空比為一半。如果這組電池帶動的是10Ω電阻，供電的10分鐘產生10A 的電流和1000W的功率，停電時電流和功率為零。