在線性回歸算法求解中，常用的是最小二乘法與梯度下降法，其中梯度下降法是最小二乘法求解方法的優化，但這并不說明梯度下降法好于最小二乘法，實際應用過程中，二者各有特點，需結合實際案例具體分析。

最后有兩份最小二乘法和邏輯斯特推導方法

1.最小二乘法求解線性回歸

線性回歸的基本模型設定為：

在此基礎上構建代價函數：

通過代價函數 求偏導并令其等于零，所得到 的即為模型參數的值：

最終得到：

這便是由最小二乘法所求得的模型參數θ的值。這里需要滿的條件是（XTX）-1存在的情況。在機器學習中，（XTX）-1不可逆的原因通常有兩種，一種是自變量間存在高度多重共線性，例如兩個變量之間成正比，那么在計算（XTX）-1時，可能得不到結果或者結果無效；另一種則是當特征變量過多，即復雜度過高而訓練數據相對較少（m小于等于n）的時候也會導致（XTX）-1不可逆。（XTX）-1不可逆的情況很少發生，如果有這種情況，其解決問題的方法之一便是使用正則化以及嶺回歸等來求最小二乘法。

2.梯度下降法求解線性回歸

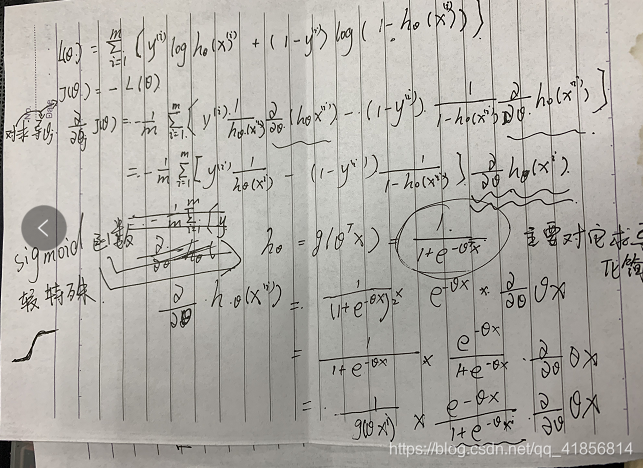
梯度下降法是一種在學習算法及統計學常用的最優化算法，其思路是對theta取一隨機初始值，可以是全零的向量，然后不斷迭代改變θ的值使其代價函數J（θ）根據梯度下降的方向減小，直到收斂求出某θ值使得J（θ）最小或者局部最小。其更新規則為：

其中alpha為學習率。J（θ）對θ的偏導決定了梯度下降的方向，將J（θ）帶入更新規則中得到：

對于上式由于每一次迭代都需要遍歷所有訓練數據一次，如果訓練數據龐大，則復雜度比較高，便使得收斂速度變得很慢，所以被稱作批量梯度下降法。當更新參數的時候，不必遍歷全部訓練數據，只要一個訓練數據就可以，這種方法會比較快地收斂，所以區別于批量梯度下降法被稱為隨機梯度下降法。

梯度下降法中學習率alpha代表了逼近最低點的速率，既不能太大也不能太小，過大可能會出現不斷地在最低點附近反復震蕩的情況，無法收斂；而過小，則導致逼近的速率太慢，即需要迭代更多次才能逼近最低點。因此，可以用一些數值試驗。

另外，在解決實際問題中，往往會出現x里的各個特征變量的取值范圍間的差異非常大，如此會導致在梯度下降時，由于這種差異而使得J（θ）收斂變慢，特征縮放便是解決該類問題的方法之一，特征縮放的含義即把各個特征變量縮放在一個相近且較小的取值范圍中，例如-1至1,0.5至2等，其中，較簡單的方法便是采用均值歸一化，也就是標準化處理。

3. 二者的應用比較

相對于最小二乘法來說，梯度下降法須要歸一化處理以及選取學習速率，且需多次迭代更新來求得最終結果，而最小二乘法則不需要。

相對于梯度下降法來說，最小二乘法須要求解（XTX）-1，其計算量為o（n3），當訓練數據集過于龐大的話，其求解過程非常耗時，而梯度下降法耗時相對較小。

所以，當模型相對簡單，訓練數據集相對較小，用最小二乘法較好；對于更復雜的學習算法或者更龐大的訓練數據集，用梯度下降法較好，一般當特征變量小于10的四次方時，使用最小二乘法較穩妥，而大于10的四次方時，則應該使用梯度下降法來降低計算量。

?

## 個人推導筆記僅供參考