一、集成算法思想
二、XGBoost基本思想
三、用python實現XGBoost算法
在競賽題中經常會用到XGBoost算法,用這個算法通常會使我們模型的準確率有一個較大的提升。既然它效果這么好,那么它從頭到尾做了一件什么事呢?以及它是怎么樣去做的呢?
我們先來直觀的理解一下什么是XGBoost。XGBoost算法是和決策樹算法聯系到一起的。?
XGBoost是boosting算法的其中一種。Boosting算法的思想是將許多弱分類器集成在一起形成一個強分類器。因為XGBoost是一種提升樹模型,所以它是將許多樹模型集成在一起,形成一個很強的分類器。而所用到的樹模型則是CART回歸樹模型
一、集成算法思想
在決策樹中,我們知道一個樣本往左邊分或者往右邊分,最終到達葉子結點,這樣來進行一個分類任務。 其實也可以做回歸任務。
該算法思想就是不斷地添加樹,不斷地進行特征分裂來生長一棵樹,每次添加一個樹,其實是學習一個新函數,去擬合上次預測的殘差。當我們訓練完成得到k棵樹,我們要預測一個樣本的分數,其實就是根據這個樣本的特征,在每棵樹中會落到對應的一個葉子節點,每個葉子節點就對應一個分數,最后只需要將每棵樹對應的分數加起來就是該樣本的預測值
?
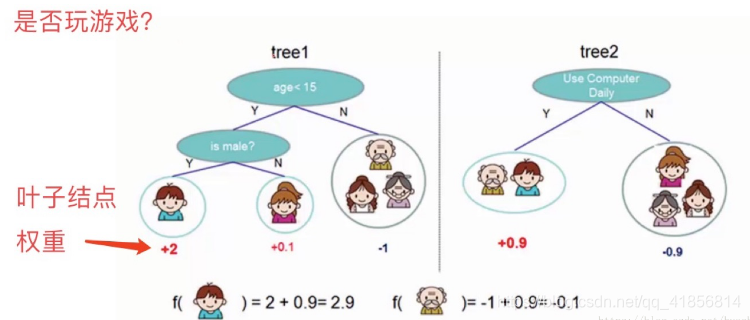
如下圖例子,訓練出了2棵決策樹,小孩的預測分數就是兩棵樹中小孩所落到的結點的分數相加。爺爺的預測分數同理
?
看上面一個圖例左邊:有5個樣本,現在想看下這5個人愿不愿意去玩游戲,這5個人現在都分到了葉子結點里面,對不同的葉子結點分配不同的權重項,正數代表這個人愿意去玩游戲,負數代表這個人不愿意去玩游戲。所以我們可以通過葉子結點和權值的結合,來綜合的評判當前這個人到底是愿意還是不愿意去玩游戲。上面「tree1」那個小男孩它所處的葉子結點的權值是+2(可以理解為得分)。
用單個決策樹好像效果一般來說不是太好,或者說可能會太絕對。通常我們會用一種集成的方法,就是一棵樹效果可能不太好,用兩棵樹呢?
看圖例右邊的「tree2」,它和左邊的不同在于它使用了另外的指標,出了年齡和性別,還可以考慮使用電腦頻率這個劃分屬性。通過這兩棵樹共同幫我們決策當前這個人愿不愿意玩游戲,小男孩在「tree1」的權值是+2,在「tree2」的權值是+0.9, 所以小男孩最終的權值是+2.9(可以理解為得分是+2.9)。老爺爺最終的權值也是通過一樣的過程得到的。
所以說,我們通常在做分類或者回歸任務的時候,需要想一想一旦選擇用一個分類器可能表達效果并不是很好,那么就要考慮用這樣一個集成的思想。上面的圖例只是舉了兩個分類器,其實還可以有更多更復雜的弱分類器,一起組合成一個強分類器。
?
二、XGBoost基本思想
XGBoost的集成表示是什么?怎么預測?求最優解的目標是什么?看下圖的說明你就能一目了然。

在XGBoost里,每棵樹是一個一個往里面加的,每加一個都是希望效果能夠提升,下圖就是XGBoost這個集成的表示(核心)。
一開始樹是0,然后往里面加樹,相當于多了一個函數,再加第二棵樹,相當于又多了一個函數...等等,這里需要保證加入新的函數能夠提升整體對表達效果。提升表達效果的意思就是說加上新的樹之后,目標函數(就是損失)的值會下降。
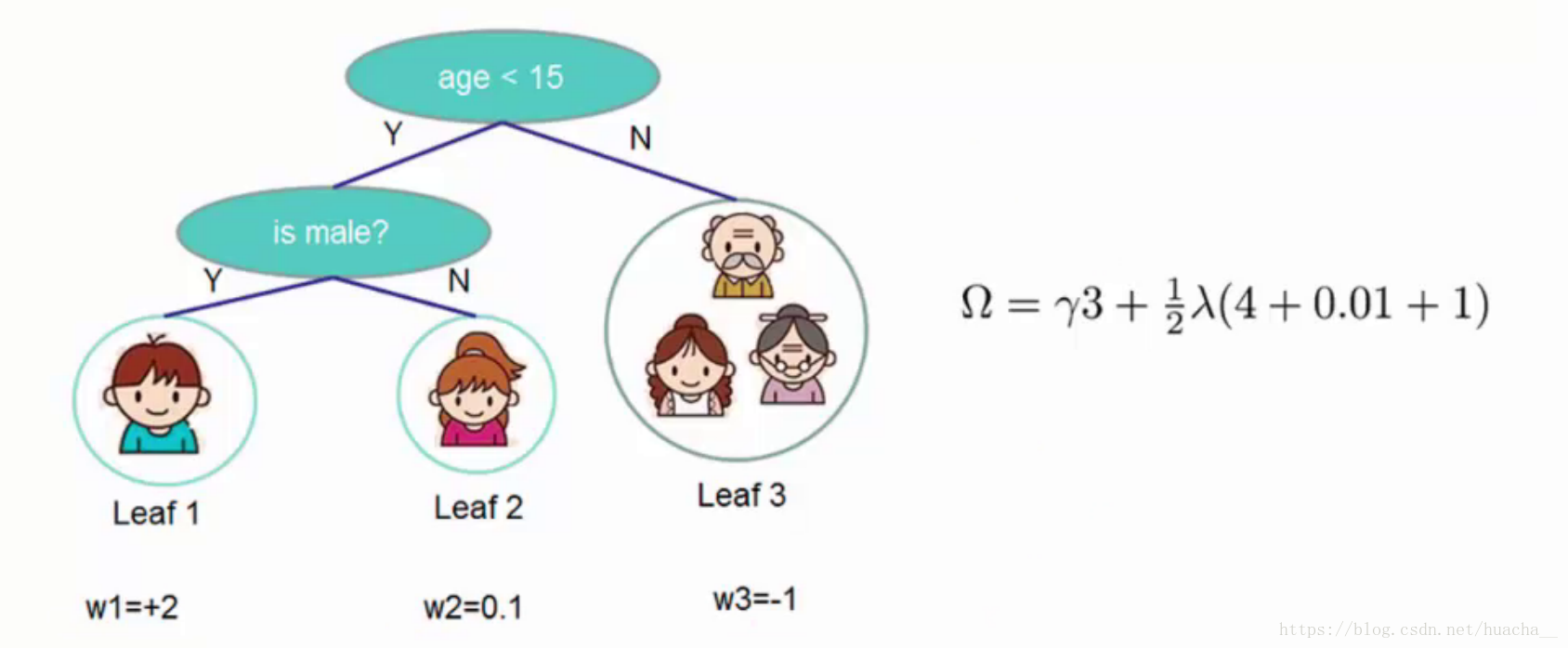
如果葉子結點的個數太多,那么過擬合的風險會越大,所以這里要限制葉子結點的個數,所以在原來目標函數里要加上一個懲罰項「omega(ft)」。
?
這里舉個簡單的例子看看懲罰項「omega(ft)」是如何計算的:
一共3個葉子結點,權重分別是2,0.1,-1,帶入「omega(ft)」中就得到上面圖例的式子,懲罰力度和「lambda」的值人為給定。
XGBoost算法完整的目標函數見下面這個公式,它由自身的損失函數和正則化懲罰項「omega(ft)」相加而成。
關于目標函數的推導本文章不作詳細介紹。過程就是:給目標函數對權重求偏導,得到一個能夠使目標函數最小的權重,把這個權重代回到目標函數中,這個回代結果就是求解后的最小目標函數值,如下:
其中第三個式子中的一階導二階導的梯度數據都是可以算出來的,只要指定了主函數中的兩個參數,這就是一個確定的值。下面給出一個直觀的例子來看下這個過程。
(這里多說一句:Obj代表了當我們指定一個樹的結構的時候,在目標上最多會減少多少,我們可以把它叫做結構分數,這個分數越小越好)
對于每次擴展,我們依舊要枚舉所有可能的方案。對于某個特定的分割,我們要計算出這個分割的左子樹的導數和和右子數導數和之和(就是下圖中的第一個紅色方框),然后和劃分前的進行比較(基于損失,看分割后的損失和分割前的損失有沒有發生變化,變化了多少)。遍歷所有分割,選擇變化最大的作為最合適的分割。
?
?GBDT與XGbost的區別
三、用python實現XGBoost算法代碼
使用天池競賽的蒸汽數據
xgboost回歸對比線性回歸 Ada、?GradientBoostingRegressor
train = pd.read_csv('./zhengqi_train.txt',sep = '\t')X = train.iloc[:,0:-1]
y = train['target']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size =0.2)from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errorlinear = LinearRegression()
linear.fit(X_train,y_train)print('r2_score',linear.score(X_test,y_test))
y1_ = linear.predict(X_test)
mean_squared_error(y_test,y1_)r2_score 0.9035544162615812
from sklearn.ensemble import AdaBoostRegressor
ada = AdaBoostRegressor()
ada.fit(X_train,y_train)print('ada_score',ada.score(X_test,y_test))
y2_ = ada.predict(X_test)
mean_squared_error(y_test,y2_)ada_score 0.8469280190502533
0.15315981475425688
from xgboost import XGBRegressor
xgb = XGBRegressor()
xgb.fit(X_train,y_train)print('xgb_score',xgb.score(X_test,y_test))
y3_ = xgb.predict(X_test)
mean_squared_error(y_test,y3_)xgb_score 0.896815295803221
0.10324391232279032
from sklearn.ensemble import GradientBoostingRegressor
gbdt = GradientBoostingRegressor()
gbdt.fit(X_train,y_train)print('gbdt_score',gbdt.score(X_test,y_test))
y4_ = gbdt.predict(X_test)
mean_squared_error(y_test,y4_)gbdt_score 0.8947755352826943
0.10528484327258612

推薦:
一文讀懂機器學習大殺器XGBoost原理



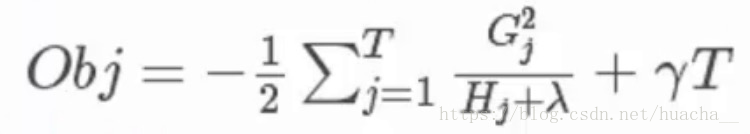
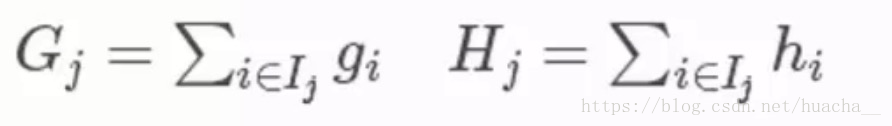









)









)



