取數游戲

題目描述

一個 $N\times M$ 的由非負整數構成的數字矩陣，你需要在其中取出若干個數字，使得取出的任意兩個數字不相鄰（若一個數字在另外一個數字相鄰 $8$ 個格子中的一個即認為這兩個數字相鄰），求取出數字和最大是多少。

輸入格式

第一行有一個正整數 $T$，表示了有 $T$ 組數據。

對于每一組數據，第一行有兩個正整數 $N$ 和 $M$，表示了數字矩陣為 $N$ 行 $M$ 列。

接下來 $N$ 行，每行 $M$ 個非負整數，描述了這個數字矩陣。

輸出格式

共 $T$ 行，每行一個非負整數，輸出所求得的答案。

樣例 #1

樣例輸入 #1

3
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1

樣例輸出 #1

271
172
99

提示

樣例解釋

對于第一組數據，取數方式如下：

$$\begin{array}{cccc}[67]& 75& 63& 10\\ 29& 29& [92]& 14\\ [21]& 68& 71& 56\\ 8& 67& [91]& 25\end{array}$$

數據范圍及約定

• 對于$20\%$的數據，$1\le N,\le 3$；
• 對于$40\%$的數據，$1\le N,M\le 4$；
• 對于$60\%$的數據，$1\le N,\le 5$；
• 對于$100\%$的數據，$1\le N,M\le 6$，$1\le T\le 20$。
• 

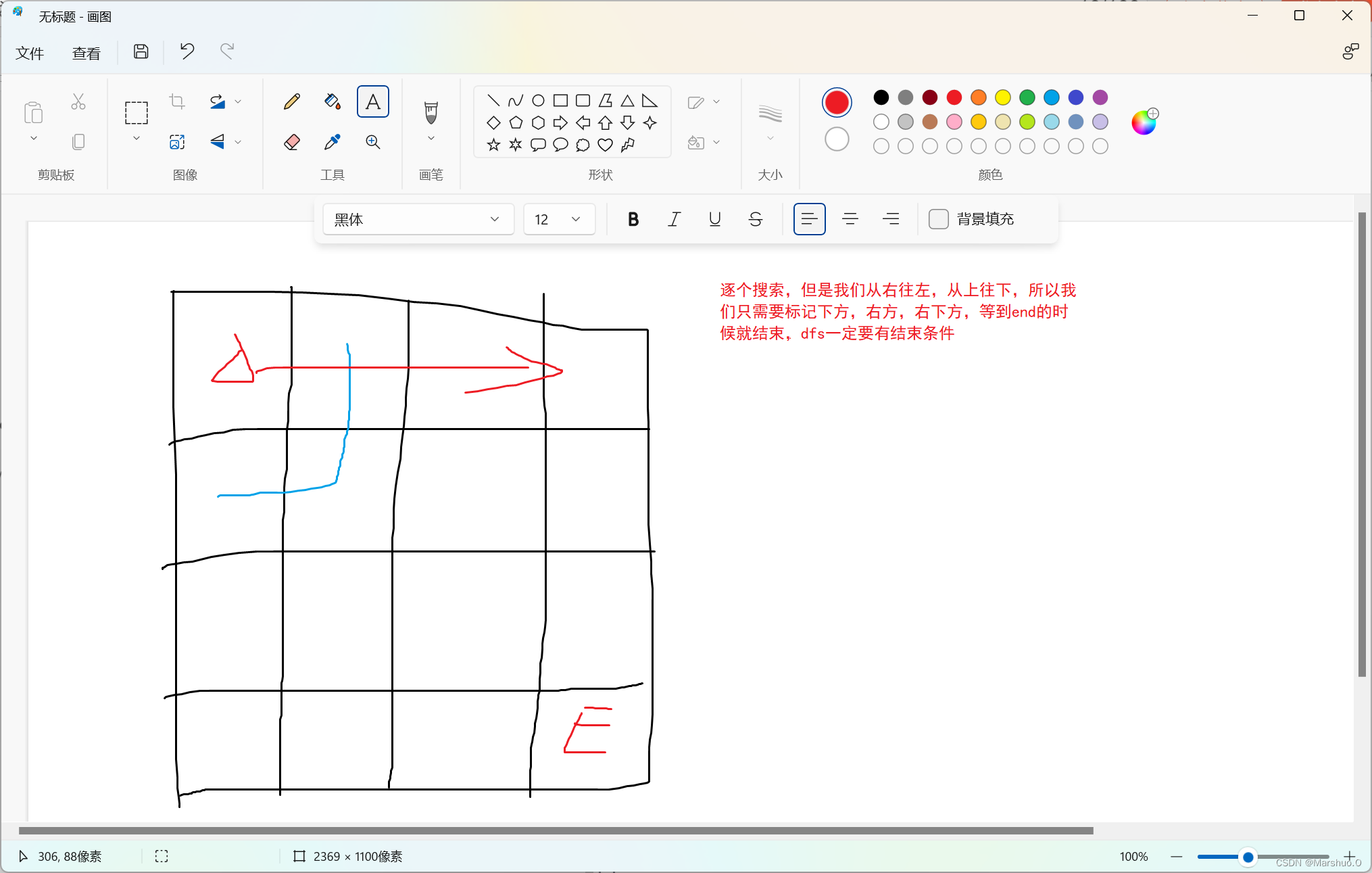
#include<bits/stdc++.h>
using namespace std;
int t,n,m,ans,maxn;
int a[37];
int vis[7][7];
void dfs(int x)
{if(x>=m*n){maxn=max(maxn,ans);return ;}dfs(x+1);if(vis[x/m+1][x%m+1]==0){ans+=a[x];for(int i=x/m;i<=x/m+2;i++){for(int j=x%m;j<=x%m+2;j++)vis[i][j]++;}dfs(x+1);ans-=a[x];for(int i=x/m;i<=x/m+2;i++){for(int j=x%m;j<=x%m+2;j++)vis[i][j]--;}}
}
int main()
{cin>>t;while(t--){cin>>n>>m;for(int i=0;i<n*m;i++)cin>>a[i];memset(vis,0,sizeof vis);dfs(0);cout<<maxn<<endl;maxn=0,ans=0;memset(a,0,sizeof a);}return 0;
}