題目描述

某鄉有n個村莊( 1 < n <= 16 )，有一個售貨員，他要到各個村莊去售貨，各村莊之間的路程s(0 < s < 1000)是已知的，且A村到B村與B村到A村的路大多不同。為了提高效率，他從商店出發到每個村莊一次，然后返回商店所在的村，假設商店所在的村莊為1，他不知道選擇什么樣的路線才能使所走的路程最短。請你幫他選擇一條最短的路。

輸入輸出格式

輸入格式：

第一行一個數n表示村莊數
接下來是一個n×n的矩陣，表示各村莊之間的路程。

輸出格式：

最短的路程。

輸入輸出樣例

輸入樣例#1：

3
0 2 1
1 0 2
2 1 0 

輸出樣例#1：

3

思路

這是一道狀壓dp，所以做這道題之前需要先知道一些關于狀態壓縮的基本概念。簡單來說，就是在一般的題目里，一個數組即可保存狀態。但是有這樣的一些題 目，它們具有DP問題的特性，但是狀態中所包含的信息過多，如果要用數組來保存狀態的話需要四維以上的數組。于是，我們就需要通過狀態壓縮來保存狀態，而 使用狀態壓縮來保存狀態的DP就叫做狀態壓縮DP。例如這道售貨員難題，若有n 個村莊，想要表示是否經過每個村莊的狀態，則需要使用n維數組，而采取狀態壓縮，往往利用二進制的整數來簡單的表示狀態，如$0101$，則表示經過了$1$、$3$號村莊，沒有經過$2$、$4$號村莊。

我先介紹一下位運算相關的知識：

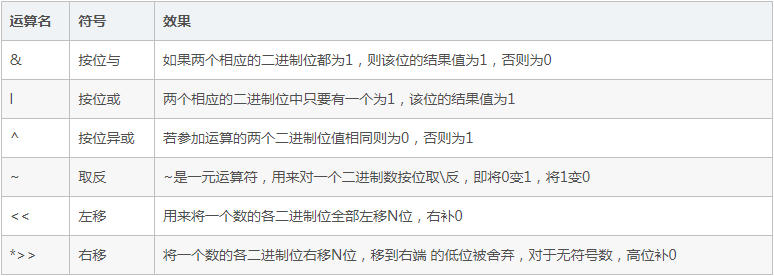
還有幾種在狀壓dp中常見的應用如下：
1.判斷一個數字x二進制下第i位是不是等于1。

方法：if ( ( ( 1 << ( i - 1 ) ) & x ) > 0)

將1左移i-1位，相當于制造了一個只有第i位上是1，其他位上都是0的二進制數。然后與x做與運算，如果結果>0，說明x第i位上是1，反之則是0。

2.將一個數字x二進制下第i位更改成1。

方法：x = x | ( 1<<(i-1) )

證明方法與1類似，此處不再重復證明。

3.把一個數字二進制下最靠右的第一個1去掉。

方法：x=x&(x-1)

回過頭來看這道題，n<20,使用狀態壓縮將會很方便，dp[i][j]表示從起始點到i號點在j狀態下花費的最短路程，例如n=3,dp[3][3]，即表示從起始點到3號點，在011，也就是經過了1號點和2號點的情況的最短路程。
詳細的狀態方程可以見代碼，再填出dp表格后，比較不同的點在經過所有點后到起始點的路程，便可以得到答案

AC代碼：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int map[21][21];
int dp[21][40000]; 
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>map[i][j];}}memset(dp,64,sizeof(dp));dp[1][1]=0;for(int i=0;i<=(1<<n);i++)//枚舉路線{for(int j=1;j<=n;j++)//枚舉村莊 {if(((1<<(j-1))&i)==0)//如果第i號村莊沒去過第j號村莊就往下 {for(int q=1;q<=n;q++)//枚舉村莊 {if(1<<(q-1)&i)//如果第i號村莊去了第q號村莊就往下 {dp[j][1<<j-1|i]=min(dp[j][1<<j-1|i],dp[q][i]+map[q][j]);//dp[j][1<<j-1|i]為：經過i號村莊去j號村莊//dp[q][i]+map[q][j]為：經過i號村莊去q號村莊，再從q號村莊去j號村莊//類似于Floyd}}}}}int ans=9999999;for(int i=2;i<=n;i++){ans=min(ans,dp[i][(1<<n)-1]+map[i][1]);//判斷從1號村莊去哪一號村莊可以更快的跑完}cout<<ans<<endl;return 0;
}