BZOJ2503: 相框

Description

P大的基礎電路實驗課是一個無聊至極的課。每次實驗，T君總是提前完成，管理員卻不讓T君離開，T君只能干坐在那兒無所事事。

先說說這個實驗課，無非就是把幾根導線和某些元器件（電阻、電容、電感等）用焊錫焊接起來。

為了打發時間，T君每次實驗做完后都在焊接一些詭異的東西，這就是他的杰作：

?

???????T君不滿足于焊接奇形怪狀的作品，強烈的破壞欲驅使他拆掉這個作品，然后將之焊接成規整的形狀。這會兒，T君正要把這個怪物改造成一個環形，當作自己的相框，步驟如下：

?

T君約定了兩種操作：

1.??????燒熔一個焊點：使得連接在焊點上的某些導線相分離或保持相連（可以理解為：把焊點上的導線劃分為若干個類，相同類中的導線相連，不同類之間的導線相離）

2.??????將兩根導線的自由端（即未與任何導線相連的一端）焊接起來。

?

例如上面的步驟中，先將A點燒熔，使得導線1與導線2、4點分離；再將D點燒熔，使得4、5與3、7相離；再燒熔E，使7與6、8相離；最后將1、7相連。

T君想用最少的操作來將原有的作品改造成為相框(要用上所有的導線)。

?

Input

輸入文件的第一行共有兩個整數n和m?—?分別表示原有的作品的焊點和導線的數量?(0 ≤?n?≤ 1 000, 2 ≤?m?≤ 50 000)。焊點的標號為1~n。?接下來的m行每行共有兩個整數?—?導線兩端所連接的兩個焊點的標號，若不與任何焊點相連，則將這一端標號為0。

原有的作品可能不是連通的。

某些焊點可能只有一根導線與之相連，在該導線的這一端與其他導線相連之前，這些焊點不允許被燒熔。

某些焊點甚至沒有任何導線與之相連，由于T君只關心導線，因此這些焊點可以不被考慮。

Output

???????輸出文件只包含一個整數——表示T君需要將原有的作品改造成相框的最少步數。

Sample Input

6 8
1 2
1 3
3 4
1 4
4 6
5 6
4 5
1 5

Sample Output

4

HINT

30%的數據中n≤10;

100%的數據中n≤1000。

這個還是挺考思路的，還要求一些圖論性質：

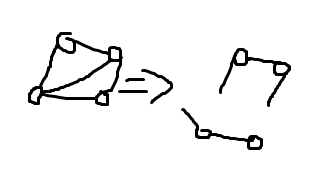
首先我們要把每個聯通塊拆開，又因為要構成一個簡單環，所以要拆成鏈狀：

像這樣

那么對于每一個歐拉回路，我們熔掉一個點就可以搞成上面n多個這東西

對于一個奇度點，我們拆一次也可以搞成這樣（題目說了隨便選邊）

然后就可以合并了

代碼如下：

//MT_LI
#include<cmath>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
int fa[110000];
int findfa(int x)
{if(fa[x]!=x)fa[x]=findfa(fa[x]);return fa[x];
}
int n,m;
int v[110000],er[110000];//是不是歐拉圖，有沒有被拆過 
int degree[110000];
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)fa[i]=i;for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);if(!x)x=++n,fa[x]=x;if(!y)y=++n,fa[y]=y;degree[x]++;degree[y]++;int fx=findfa(x),fy=findfa(y);if(fx==fy)continue;fa[fy]=fx;}int ans=0,sum=0;for(int i=1;i<=n;i++){if(!degree[i])continue;if(degree[i]&1){sum++;er[findfa(i)]=1;}    if(degree[i]>2){ans++;v[findfa(i)]=1;}}int cnt=0;for(int i=1;i<=n;i++)if(fa[i]==i&&degree[i])cnt++;for(int i=1;i<=n;i++)if(cnt>1&&degree[i]&&fa[i]==i&&!er[i]){sum+=2;if(!v[i])ans++;}printf("%d\n",ans+sum/2);return 0;
}

?

?