代理ARP（Proxy-arp）的原理就是當出現跨網段的ARP請求時，路由器將自己的MAC返回給發送ARP廣播請求發送者，實現MAC地址代理（善意的欺騙），最終使得主機能夠通信。
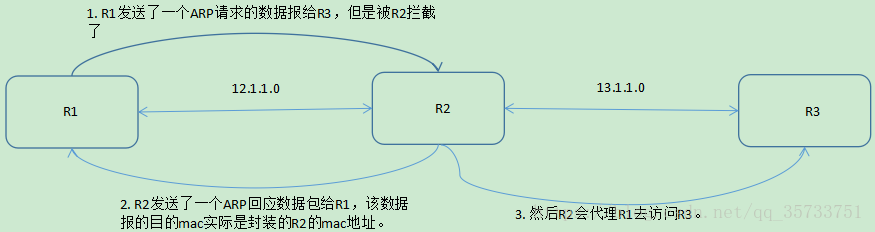
圖中R1和R3處于不同的局域網，R1和R3在相互通信時，R1先發送了一個ARP廣播數據包，請求R3的mac地址，但是由于R1是12.1.1.0網段，而R3是13.1.1.0網段，R1和R3之間是跨網段訪問的，也就是說R1的ARP請求會被R2攔截到，然后R2會封裝自己的mac地址為目的地址發送一個ARP回應數據報給R1（善意的欺騙），然后R2就會代替R1去訪問R3。
??整個過程R1以為自己訪問的是R3，實際上真正去訪問R3的是R2，R1卻并不知道這個代理過程，這就是所謂的ARP代理，通常用于跨網段訪問。
??注意：如果R2關閉了arp的代理功能，那么R1再訪問R3的時候，R2并不會把自己的mac地址給R1，那么R1和R3之間就無法通信。默認情況下，思科的設備是開啟了arp代理功能，也就是說，R2會作為中間代理實現R1和R3之間跨網段通信。
??代理ARP的使用場景為：1. 沒有路由功能的主機，2. 有路由功能，目的地指向本地出口
?
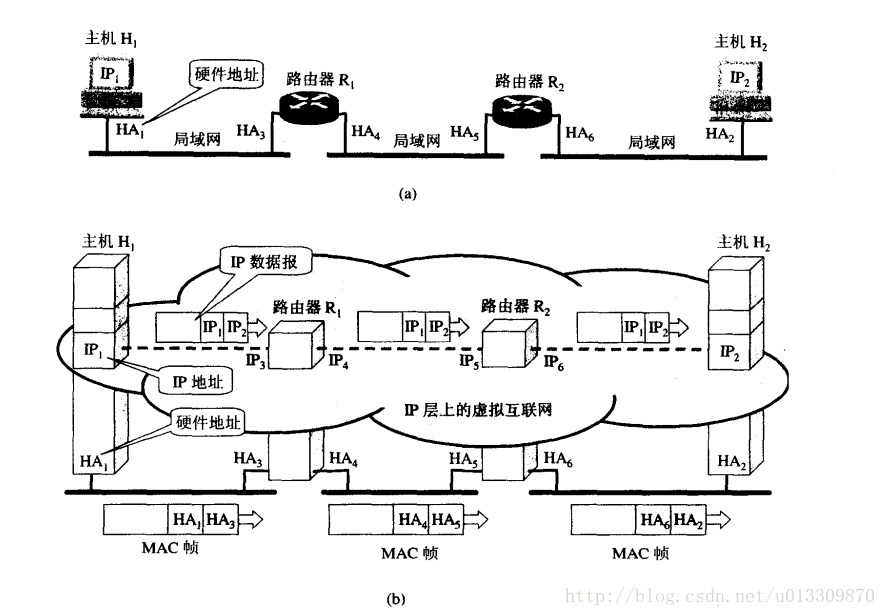
注意：在點對點鏈路中不使用ARP，實際上在點對點網絡中也不使用MAC地址，因為在此類網絡中分別已經獲取了對端的IP地址。
?
代理ARP是ARP協議的一個變種。 對于沒有配置缺省網關的計算機要和其他網絡中的計算機實現通信，網關收到源計算機的 ARP 請求會使用自己的 MAC 地址與目標計算機的 IP地址對源計算機進行應答。代理ARP就是將一個主機作為對另一個主機ARP進行應答。它能使得在不影響路由表的情況下添加一個新的Router，使得子網對該主機來說變得更透明化。同時也會帶來巨大的風險，除了ARP欺騙，和某個網段內的ARP增加，最重要的就是無法對網絡拓撲進行網絡概括。代理ARP的使用一般是使用在沒有配置默認網關和路由策略的網絡上的
?
)
