目標檢測是一種基于目標幾何和統計特征的圖像分割，最新的進展一般是通過R-CNN（基于區域的卷積神經網絡）來實現的，其中最重要的方法之一是Faster R-CNN。
1.?總體結構
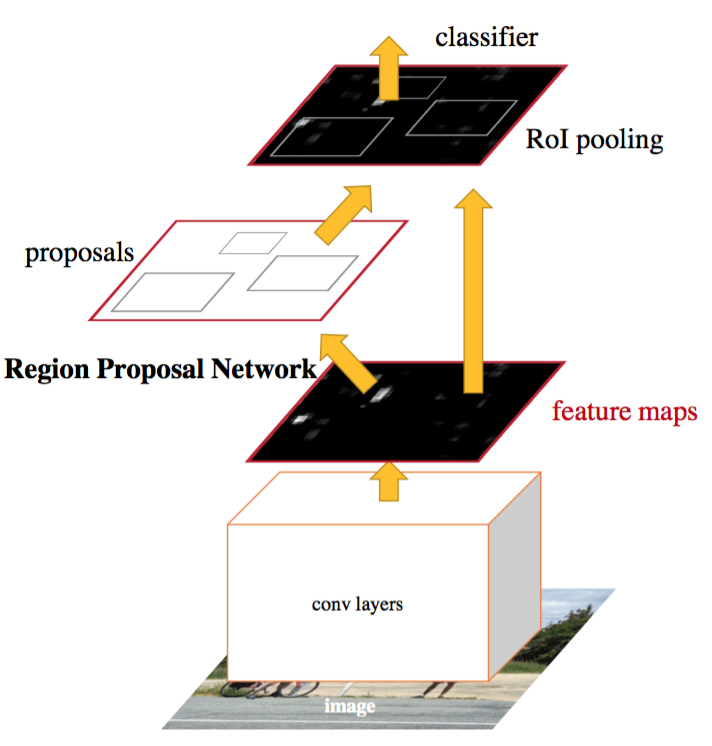
Faster R-CNN的基本結構如下圖所示，其基礎是深度全卷積網絡（ZF或者VGG-16）。在深度全卷積網絡輸出的特征圖（Feature Map）上，增加了區域提議網絡（RPN，Region Proposal Network），該網絡的主要任務是提出Proposals。根據提出的這些Proposals對特征圖進行裁剪，當然對不同區域裁剪以后的尺寸是不一致的，因此需要進行RoI池化（RoI Pooling），轉換成統一的尺寸，最終得到每個區域的分類。
?
轉載于:https://www.cnblogs.com/mstk/p/9879175.html
本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。 如若轉載，請注明出處：http://www.pswp.cn/news/388091.shtml 繁體地址，請注明出處：http://hk.pswp.cn/news/388091.shtml 英文地址，請注明出處：http://en.pswp.cn/news/388091.shtml
如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！
