第一章 ? 轉自http://www.cnblogs.com/batteryhp/p/4654860.html
思考題
1-1(運行時間的比較)確定時間t內求解的問題的最大規模。

上面是網上提供的答案。
注意點:
1、最左邊一列的是關于n的增長情況描述,值得記住的是這些增長的排列順序,這是非常有用的,啊,數分學好了會很容易;
2、注意1s內能處理的以n為增長量級的規模是10的6次方,記住這個結果可以推導出其他增長量級的處理規模;
3、注意這里的lg指的是以2為底的對數函數。
順便做了一張lgn的增長圖,感受一下:
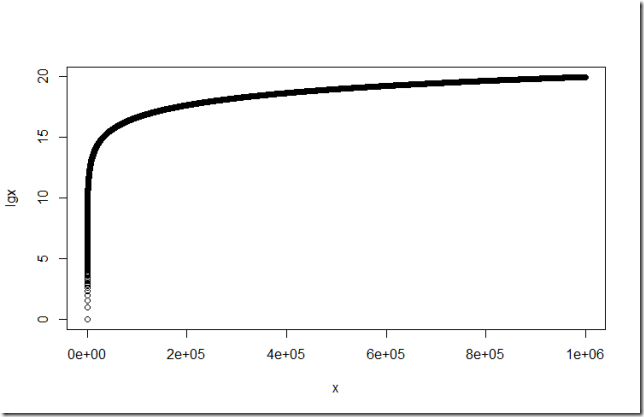
本來想把n和nlgn畫在一起,可是效果不滿意啊,如下圖:
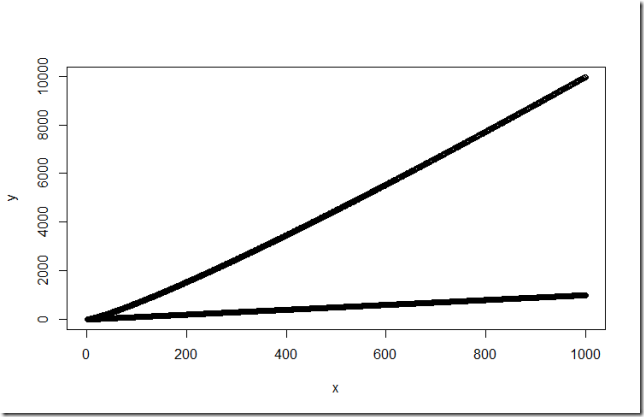
看得出,nlgn比n增長的快不少啊!(貌似)
第二章
2.1
2、重寫INSERTION-SORT使之按照升序排列。
其實,只要將while步中的>改成<即可。
//INSERTION-SORT for j = 2 to A.lengthkey = A[j]i = j - 1while i > 0 and A[i] < keyA[i+1] = A[i]i = i - 1A[i+1] = key
3、查找問題,在數組中查找一個數,線性查找,寫偽代碼,并證明循環不變式。
//find some value for i = 1 to A.lengthif v == A[i]return ielse return NIL
4、兩個二進制數存儲在兩個數組中,將這兩個數加和,并將和存儲到另一個數組中,寫出形式化描述并且寫出偽代碼。
寫出代碼(親測有效):
#include <iostream>using namespace std;
const int Num = 10;int main()
{int a[Num] = {1,0,1,1,0,1,1,0,1,1};int b[Num] = {0,1,1,1,0,1,0,1,1,1};int c[Num + 1] = {0};int flag = 0;int i;for(i = Num-1;i >= 0;i--){c[i+1] = a[i] + b[i] + flag;if(c[i+1] > 1){c[i+1] = c[i+1]%2;flag = 1;}elseflag = 0;}c[0] = flag;for(i = 0;i <= Num;i++)cout << c[i];cout << endl;return 0;
} ?
2.2
1、theta(n^3)
2、排序一個n個數的數組,規則是這樣的,將最小的跟第一個交換,余下最小的的跟第二個交換…一直做下去,一直到n-1,這個算法叫做選擇算法,要求寫出循環不變式和偽代碼,寫出最好最壞運行時間的量級。
//選擇算法偽代碼 for i = 1 to n - 1min = A[i]for j = i + 1 to nif A[j] < minmin = A[j]exchange A[i] and min
下面是答案上的一種寫法,道理是一樣的:
?

另外,最好和最壞時間要寫一下。最好無非是已經排好了,這時候也沒用啊,也要尋找最小值……所以,最好最壞都是n^2.
3、考慮2.1-3的線性查找問題,假定要查找的元素等可能地為數組中的任意元素,平均需要檢查輸入序列的多少元素?最壞情況又如何?
解:直觀想法,平均的話就是半數的元素數量;最壞就是全部。可以這么想,現在要從中選一個元素,每個元素出現的概率是1/n,需要檢查的個數分別為1個,2個...n個,那么取期望,就是(1+2+3...+n)/n 為(n+1)/2個元素;最壞情況就是n個,沒什么好說的。換句話說,都是theta(n)的復雜度。
按照答案上的說法,由于一般時間在前一半數組中尋找,一半時間在后一半數組中尋找,那么那么平均下來就是中間那個值嘍~~
4、我們可以如何修改(幾乎所有的)算法可是使之有最好的運行時間?
解:想法:就是最好的輸入唄。。。看一下答案:One can modify an algorithm to have a best-case running time by specializing it to handle a bestcase input efciently.哦。。。
2.3
2、重寫MERGE,當L或者R為空時,把另一組的數據全部復制到A中。
//MERGE 偽代碼 n1 = q - p + 1 n2 = r - q Let L[1..n1] and R[1..n2] be new arrays //由于不需要“哨兵牌”,無需多出一個元素 for i = 1 to n1L[i] = A[p + i -1] for j = 1 to n2R[j] = A[q + j]i = 1 j = 1for k = p to rif i > n1 //在這里加兩個判斷while j <= n2A[k] = R[j]k = k + 1 //不要忘了將k和j遞增,這里的k和j得分開遞增j = j + 1breakif j > n2while i <= n1A[k] = L[i]k = k + 1i = i + 1breakif(i < n1 and j < n2) //注意這里的條件判斷,不能直接將二級的if else 拿上來,否則混亂
if L[i] <= R[j]A[k] = L[i]i = i + 1else A[k] = R[j]j = j + 1
//沒有“哨兵牌”的代碼
#include <iostream>
#include <time.h>void MERGESORT(int*, int,int);
void MERGE(int*,int,int,int);using namespace std;int main()
{clock_t start, end;start = clock();int i;int* arr = new int[100];for (i = 0; i < 100; i++){arr[i] = 100 - i;}MERGESORT(arr,0,99);for (i = 0; i < 100; i++){cout << arr[i] << " ";if (i % 10 == 9){cout << "\n";}}delete[]arr;cout << "__________________" << endl;end = clock();cout << "Run time: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;return 0;
} void MERGESORT(int* a, int p, int r)
{int q;if (p < r){q = (p + r) / 2;MERGESORT(a, p, q);MERGESORT(a, q + 1, r);MERGE(a, p, q, r);}
}void MERGE(int* arr, int p, int q, int r)
{int n1 = q - p + 1;int n2 = r - q;int* Left = new int[n1];int* Right = new int[n2];int i, j;for (i = 0; i < n1; i++)Left[i] = arr[p + i];for (j = 0; j < n2; j++)Right[j] = arr[q + j + 1];i = 0;j = 0;for (int k = p; k <= r; k++){if (i >= n1){while (j < n2){ arr[k] = Right[j];k++;j++;}break;}if (j >= n2){while (i < n1){ arr[k] = Left[i];k++;i++;}break;}if (i < n1 && j < n2){if (Left[i] <= Right[j]){arr[k] = Left[i];i++;}else{arr[k] = Right[j];j++;}}}delete []Left;delete []Right;} 3、利用數學歸納法證明下面的式子成立,其中T(n)=nlgn:
![]()
證明:
(1)基本情況,n = 2時,T(n)=2lg2=2成立;
(2)假設當n = 2^k 時成立,即T(2^k) = (2^k)lg(2^k),下面證明當 n = 2^(k + 1)時成立。T(2^(k+1)) = 2T(2^k)+2^(k+1)=2((2^k)lg(2^k))+2^(k+1)=2^(k+1)(lg(2^k)+1)=2^(k+1)(lg(2^k)+lg2)=2^(k+1)(lg(2^k * 2))=2^(k+1)(lg(2^(k+1))),n=2^(k+1)時也成立。
4、我們可以把插入排序表示為以下一個遞歸過程。為了排序A[1..n],遞歸地排序A[1..n-1],然后把A[n]插入到已經排序的數組A[1..n-1]中。為插入排序的這個遞歸版本的最壞情況寫一個遞歸式。
解:我們考慮最倒霉的情況,在插入排序中,原數組是按照倒序排列的,那么每次有一個新的數,就得讓它跑到已經排好的數組的最前面……那么新插入一個元素時的時間復雜度就是theta(n),因為總要比較n-1次,再加上判斷下標不越界,復雜度就是n了:
![]()
5、回顧查找問題,2.1-3,注意到如果A已經被排序了,那么新的值v可以先與A的中間元素進行比較,那么根據比較的結果原數組中的一半就可以不再考察了。二分查找算法就是不斷重復這個過程,每次的序列數量減半。寫出二分查找的迭代或者遞歸的偽代碼,并且證明最壞運行時間為theta(lgn).
解:需要注意的是,被查找的數組必須是已經排序好的數組。
//遞歸版本的二分查找 BINARYSEARCH(A,v,p,r) if p >= r and A[p] != vreturn NIL else q = (p + r)/2if A[q] == vreturn qelse if A[q] < vreturn BINARYSORT(A,v,q+1,r)else return BINARYSORT(A,v,p,q-1)
//遞歸版本二分查找代碼
#include <iostream>
#include <time.h>using namespace std;int Binarysearc(int*, int, int, int);int main()
{clock_t start, end;start = clock();int* arr = new int[100];int v = 70;for (int i = 0; i < 100; i++){arr[i] = i;}int position = Binarysort(arr, v, 0, 99);cout << position << endl;delete[]arr;cout << "__________________" << endl;end = clock();cout << "Run time: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;return 0;}int Binarysearch(int* arr, int v, int p, int r)
{if (p > r && arr[p] != v)return -1;else{int q = (p + r) / 2;if (arr[q] == v)return q;else if (arr[q] < v)Binarysort(arr, v, q + 1, r);elseBinarysort(arr, v, p, q - 1);}} 關于迭代版本:
//迭代版本的二分查找 A is a array v is a value p,r are the min and max index of A ITERATIONSEARCH(A,v,p,r)while(p <= r)q = (p + r)/2if A[q] == vreturn qelse ifv < A[q]r = qelsep = qreturn NIL
//迭代版本的二分查找
#include <iostream>
#include <time.h>using namespace std;int Iterattionsearch(int*, int, int, int);int main()
{clock_t start, end;start = clock();int* arr = new int[100];int v = 70;for (int i = 0; i < 100; i++){arr[i] = i;}int position = Iterattionsearch(arr, v, 0, 99);cout << position << endl;delete[]arr;cout << "__________________" << endl;end = clock();cout << "Run time: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;return 0;}int Iterattionsearch(int* arr, int v, int p, int r)
{while (p <= r){int q = (p + r) / 2;if (arr[q] == v)return q;else if (arr[q] < v)p = q + 1;elser = q - 1;}} 下面考察其最壞時間的復雜度:
元素個數為n的數組,最壞需要除2*lgn次2才會得到結果,故最壞時間復雜度為theta(lgn).這樣考慮m分查找,其時間復雜度為m*lgm(n).lgm是以m為底的對數函數,那么對于給定的n,m是多少時時間最短呢?做了一些實驗,表明m=3的時候函數m*lgm(n)最小,或者說時間復雜度最低,但是效率據說不是最高的。有空試一試~
?
6、在插入排序中,對于已經排好序的A[1..n-1],需要線性掃描這個已經排好的序列。現在要對插入排序進行優化,將這個線性排序的部分改成二分查找的方式,使最壞時間變為theta(nlgn)(原來是theta(n^2))如何實現呢?
解:第一想法,不可能吧…畢竟需要一個一個往后挪位置啊……
yep,看了看其他人的答案,確實是這樣的,即使可以使用二分查找找到位置,但是后面移位的過程時間復雜度仍然是theta(n),整體的復雜度還是theta(n^2).
7、請給出一個復雜度為theta(nlgn)的算法,給定n個整數的集合S和另一個整數x,該算法能確定S中是否存在兩個其和剛好為x的元素。
解:自己的想法:先排序(歸并排序),然后第一個數從前面開始找,那么x減去這個數的結果就是需要找的數,再用二分查找去找這個數!總的復雜度就是theta(nlgn).
yep,看了下答案確實是這樣。
截圖一下:

思考題
2-1(在并歸排序中對小數組采用插入排序)雖然歸并排序的最壞運行時間是theta(nlgn),而插入排序的最壞運行時間是theta(n^2),但是插入排序中的常數因子可能使得在n較小時運行時間更短。因此在并歸排序中當子問題編的足夠小時,采用插入排序使得遞歸的葉變粗是有意義的。考慮對歸并排序的修改,其中使用插入排序來排序長度為k的n/k個子表,然后使用標準的合并機制來合并這些子表,這里k是一個特定的值。
a.證明:插入排序最壞情況可以在theta(nk)時間內排序每個長度為k的n/k個子表。
b.表明在最壞情況下如何在theta(nlg(n/k))時間內合并這些子表。
c.假定修改后的算法的最壞情況運行時間為theta(nk+nlg(n/k)),要使修改后的算法與標準的歸并排序具有相同的運行時間,作為n的一個函數,借助theta記號,k的最大值是什么?
d.在實踐中,我們應該如何選擇k?
解:打完上面的思考題,感覺……跟練習題不是一個次元的!臥槽,太有挑戰性。
a.證明:每個子表的時間復雜度為theta(k^2),共有n/k個子表,故總時間為theta(nk).
b.n/k個列表兩兩合并,合并完繼續合并,共需要lg(n/k)層,每層時間復雜度均為theta(n),所以合并共需要theta(nlg(n/k))的時間。
c.標準的歸并排序的時間復雜度為theta(nlgn),需要theta(nlgn)=theta(nk+nlg(n/k)),這時候k的最大值只能是k=theta(lgn).
d.k的選取標準是長度為k的子列,插入排序要比歸并排序快。額,這么說好像不負責任。。。(這里需要用紙來演算一下)
網上有一個答案可能靠譜:這是個實驗問題,應該在k的合法范圍內測試可能的k,用T-INSERTION-SORT(k)表示k個元素的插入排序時間,T-MERGE-SORT(k)表示k個元素的合并排序時間。該問題等價于測試求解T-INSERTION-SORT(k)/T-MERGE-SORT(k)比值最小的k值。
下面這段話來自:http://blog.kingsamchen.com/archives/715
由反證法可以得到,k的階取值不能大于Θ(logn),并且這個界可以保證插排優化的漸進時間不會慢于原始歸并排序。
由于對數函數的增長特點,結合實際排序規模,k得實際取值一般在10~20間。
在歸并中利用插入排序不僅可以減少遞歸次數,還可以減少內存分配次數(針對于原始版本)。
?
ps.需要對比驗證一下。
2-2(冒泡排序的正確性)冒泡排序是一種流行但低效的排序算法,它的作用是反復交換相鄰的未按次序排列的元素。
//冒泡排序偽代碼
BUBBLESORT(A) for i = 1 to A.length -1 for j = A.length downto i + 1if A[j] < A[j - 1]exchange A[j] with A[j - 1]
a.假設A’是BUBBLESORT(A)的輸出。為了證明BUBBLESORT正確,我們必須 證明它將終止并且有:
A'[1] <= A'[2]...<= A'[n] (2.3)
其中n=A.length.為了證明BUBBLESORT確實完成了排序,我們還需要證明什么?下面兩部分將證明不等式(2.3)。
b.為第二層的for循環精確地說明一個循環不變式,并證明該循環不變式成立。你的證明應該使用本章中給出的循環不變式的結構。
c.使用(b)部分證明的循環不變式的終止條件,為第一層說明一個循環不變式,這個不變式就能證明式子(2.3)。證明中應該使用本章中給出的循環不變式證明的結構。
d.冒泡排序的最壞情況運行時間是多少?與插入排序的運行時間相比,性能如何?
解:
b.第二層循環使得將未排序的數組中最小的一個移動到最前面。
初始:j=n,子數組為A[j-1..n]=A[n-1..n]有兩個元素。在循環內部,通過條件交換語句,可以保證A[n-1] < A[n]成立。因此A[j-1]是A[j-1..n]中的最小元素。 保持:每次迭代開始時,A[j]是A[j..n]中的最小元素。在迭代操作中,當A[j] < A[j-1]時交換,因此總有A[j-1] < A[j]。可知,本次迭代操作完成后,A[j-1]一定是A[j-1..n]中的最小元素。 終止:j=i+1時退出,因此結束時,A[i]一定是A[i..n]中的最小元素。http://blog.csdn.net/cppgp/article/details/7161701
c.第一層循環使得不斷增加已經排序好的數組元素,知道全部排好。
初始:i=1,是A中的第一個元素,因此內部循環完成后,可以保證A[1]中保存A[1..n]的最小元素。 保持:每次遞增i時,執行內部循環,因此A[i]中保存A[i..n]中的最小元素。可知每次內部循環完成后,都有 A[1] ≤ A[2] ≤ ... ≤ A[i] 終止:i=length[A]時終止,此時有 A[1] ≤ A[2] ≤ ... ≤ A[n]。轉自:http://blog.csdn.net/cppgp/article/details/7161701
d.兩個的最壞運行時間都是theta(n^2),但是在插入排序中,最好的時間可以達到theta(n),冒泡排序一直是theta(n^2).
2-3(霍納(Horner)規則的正確性)給定系數a0,a1,a2,…,an和x的值,代碼片段
y = 0 for i = n downto 0y = ai + xy
實現了用于求值多項式
![]()
的霍納規則.
ps.在中國,這個算法叫做秦九韶算法。
a.借助theta符號,實現霍納規則的以上代碼片段的運行時間是多少?
b.編寫偽代碼來實現樸素的多項式求值算法,該算法從頭開始計算多項式的每項。該算法的運行時間是多少?與霍納規則相比,其性能如何?
c.考慮以下循環不變式:
在第2-3行for循環每次迭代的開始有
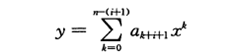
把沒有項的和式解釋為等于0.遵照本章中的循環不變式證明的結構,使用該循環不變式來證明終止時有
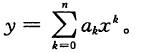
d.最后證明上面給出的代碼片段將正確地求由系數a0,a1,a2,a3…,an刻畫的多項式。
解:啊啊啊,多項式求值的問題,原來換一種寫法就是一種新規則,霍納規則。
a.這應該是theta(n)吧……很顯然的;n次多項式用到n次加法,n次乘法。
b.偽代碼如下:
//多項式一般求解偽代碼 y = 0 for i = 1 to nbase = 1for j = 1 to i base = base*xy = y + ai*base y = y + a0 return y
上述偽代碼的復雜度是theta(n^2)(1+2+3+…+n),顯然霍納規則比一般算法好得多,霍納算法是theta(n)啊,那么問題來了:霍納算法節省了哪一部分的運算呢?還能不能更簡化呢?
自己想一想,一般的算法重復計算了好多次x的乘方,每一次乘方都需要重新計算,而霍納算法通過改變計算順序,成功避免了這一問題(trick在哪里?還沒想明白)。我想到一個辦法,一般算法的每次結果存起來再用!這樣的復雜度也是theta(n),不過這也有存儲的問題,偽代碼:
//多項式改進偽代碼 y = 0 arr[n+1] arr[0] = 1 for i = 1 to n arr[i] = a[i-1]*xy = y + ai * arr[i] y = y + a0 return y
c.題目的敘述是對的,進行了驗證,除了第一步遇到-1次項外,感覺比較巧妙,利用循環不變式可以證明。
初始:i=n,y[n] = 0,迭代開始時,循環后有y[n] = a[n]。 保持:對于任意 0 ≤ i ≤ n,循環后有:y[i] = a[i] + y[i+1] * x = a[i] + (a[i+1] * x + a[i+2] * x + ... + a[n] * x^(n-(i+1))) * x= a[i] + a[i+1] * x + a[i+2] * x^2 + ... + a[n] * x^(n-i) 終止:i小于0時終止,此時有 y[0] = a[0] + a[1] * x + a[2] * x^2 + a[n] * x^n證明和y = Σ a[k+i+1] * x^k的關系:k 從0到n-(i+1),等價于 0 ≤ k ≤ n-(i+1)。因此y = Σ a[k+i+1] * x^k= a[i+1] + a[i+2] * x + ... + a[n-(i+1)+i+1] * x^(n-i)= a[i+1] + a[i+2] * x + ... + a[n] * x^(n-i)由于i+1循環之后和i循環之前的值相等,用y'[i]表示i循環之前的值,則有:y'[i] = y[i+1]霍納規則循環不變式的結果表明:y[i] = a[i] + a[i+1] * x + a[i+2] * x^2 + ... + a[n] * x^(n-i)因此有:y'[i] = y[i+1] = a[i+1] + a[i+2] * x + ... + a[n] * x^(n-(i+1))令k=n-(i+1),則n=k+i+1,所以:y'[i] = a[i+1] + a[i+2] * x + ... + a[k+i+1] * x^(k+i+1-(i+1))= a[i+1] + a[i+2] * x + ... + a[k+i+1] * x^k用y表示y'[i],則有:y = a[i+1] + a[i+2] * x + ... + a[k+i+1] * x^k= Σ a[k+i+1] * x^k其中 k從0到n-(i+1)證畢。轉自:http://blog.csdn.net/cppgp/article/details/7161701
上面的證明很細致,再次感謝。
d.這一步把循環不變式寫到0就可以了,c中已經證明了,在第二個證明里。
2-4(逆序對)假設A[1..n]是一個有n個不同數的數組。若 i < j 且 A[i] > A[j],則對偶(i,j)稱為A的一個逆序對(inversion)。
a.列出數組<2,3,8,6,1>的5個逆序對。
b.由集合{1,2,…,n}中的元素構成的什么數組具有最多的逆序對?它有多少逆序對?
c.插入排序的運行時間與輸入數組中逆序對的數量之間是什么關系?證明你的回答。
d.給出一個確定在n個元素的任何排列中逆序對數量的算法,最壞情況需要theta(nlgn)時間。(提示:修改歸并排序)
解;
a.說白了就是前面比后面大,那么就有 (1,5),(2,5),(3,4),(3,5),(4,5).
b.啊啊啊,都讓開,讓我來回答這個題!
哈哈,大家記不記得高等代數里面在講矩陣按行或者按列展開的時候,每一項的正負號怎么決定的?--對了,就是-1的這個元素(所在行+所在列)次方!好像跟這個題沒什么關系哈。。。不過下面這個就很有關系了:在近世代數里面,在學對換群的時候接觸過這方面的內容,好吧,我忘了是哪一塊內容了,待我查查或者問問別人。。
那么這個題目呢,顯然數組逆序排的時候逆序對最多啦~~最多的個數呢,就是 從右向左數 1+2+3…+n-1=n(n-1)/2對。
c.這個問題用歸納法想一下,沒有逆序對的時候時間是n,逆序排的時候是n^2,那么中間呢?啊,是這樣,移動的次數不用考慮,只要考慮比較的次數就可以了,比較的越多,移動的就越多,這個比較的次數決定了插入排序的運行時間,而且造成比較的原因就是逆序對了,所以對于已經排好的A[1..n-1]而言,A[n]比A[1..n-1]中小的個數就是比較的次數(其實應該是比較次數-1),這么說來從第一個數開始想,總的逆序對數目就是需要進行比較的總數了。
d.想了半天,由于合并總共lgn層,那么每一層求逆序對的復雜度就是n,從網上看了幾個答案,好像沒有幾個好好寫的,找到了一個挺好,說一說想法。加入左右兩個子數組已經排好序,那么只要從右面數組中選出一個,那么現在左邊數組中對應的剩下的那一部分都比剛才從右邊選出的大,那么對應的逆序對就多出左邊剩下元素的數量那么多個。ps.在此問題中,在子序列合并之前,每一個排好的子序列自身數組中的逆序對已經在上一步求出,合并的過程是在求子序列之間的逆序對數量。
inversions = 0 //全局變量
COUNT-INVERSIONS(A,p,r)
if p < rq = (p + r)/2COUNT-INVERSIONS(A,p,r)
COUNT-INVERSIONS(A,p,r)
MERGE-INVERSIONS(A,p,q,r)
MERGE-INVERSIONS(A,p,q,r) n1 = q - p + 1 n2 = r - q let L[1 : : n1 + 1] and R[1 .. n2 + 1] be new arrays for i = 1 to n1L[i ] = A[p + i - 1] for j = 1 to n2R[j] = A[q + j] L[n1 + 1] = ∞ R[n2 + 1] = ∞ i = 1 j = 1for k = p to rif L[i] > R[j] A[k] = R[i]
inversiongs = inversiongs + n1 – i + 1 i = i + 1else A[k] = R[j] j = j + 1
思想轉自:http://www.cnblogs.com/lilith/archive/2012/11/21/2780319.html,自己作了修改。上面的算法還需要程序驗證,這是下一步的工作,下一步要把前面提到的偽代碼實現一遍。這一篇寫的太長了。




















