
當學習完矩陣的定義以后,我們來學習矩陣的基本運算,與基本性質

矩陣的基本運算:矩陣的加法,每一個對應元素相加,對應結果的矩陣

例子:矩陣A和矩陣B表示的是同學上學期和下學期的課程的成績,兩個矩陣相加就表示一學年科目成績的總和

矩陣的數量乘法:一個數乘于一個矩陣
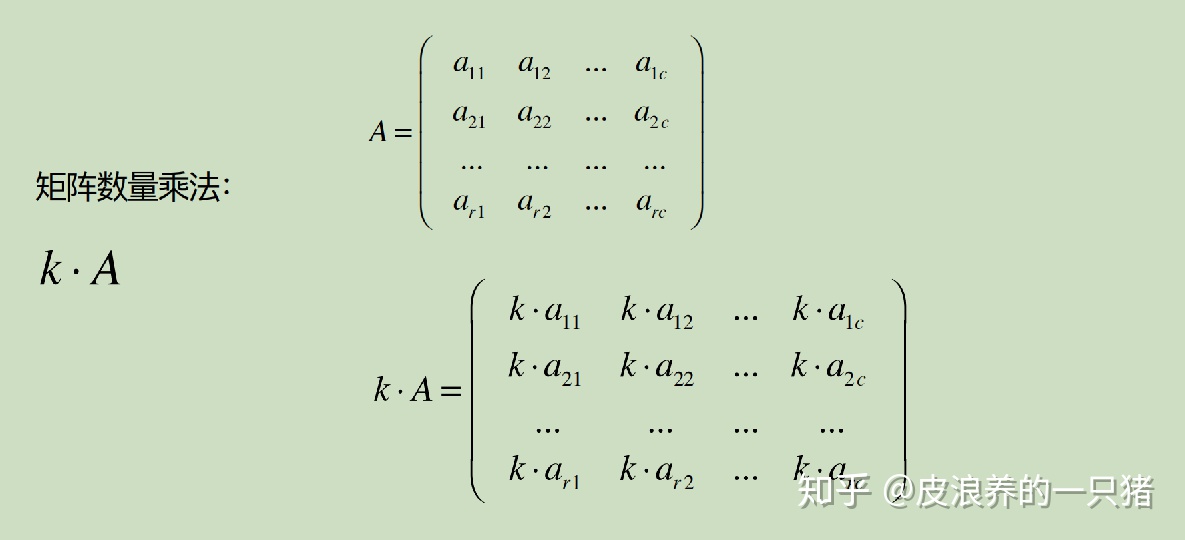
還是接著上面學生成績的例子:

矩陣數量乘法可以理解為,求兩學期學生科目成績的平均分1/2(A+B),因為之前我們已經算出了一學年科目的成績總和,現在只需要乘于二分之一就可以了。
矩陣的數量乘法還有一個幾何的直觀理解:
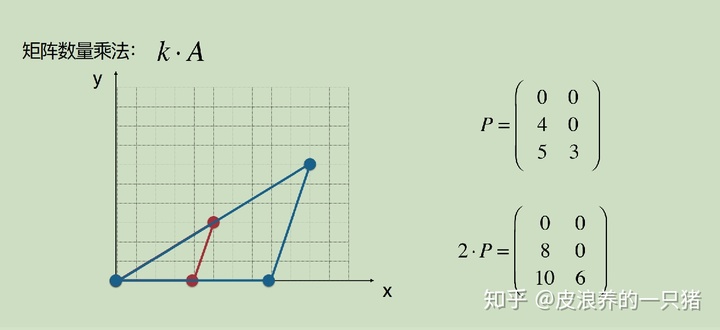
下圖的矩陣P可以理解為3個行向量組成,這3個行向量表示的是二維平面坐標系中的一個點,就是表示一個三角形,矩陣的數量乘法2.P之后,這個三角形就縮放變大了
矩陣的基本運算性質

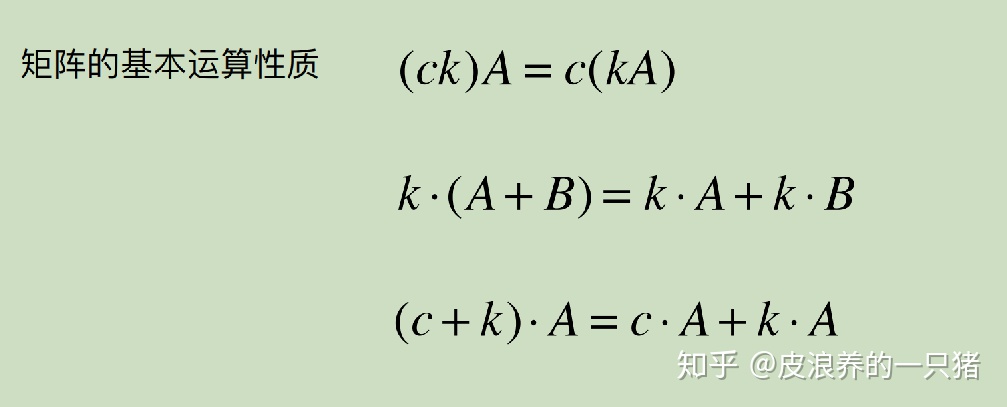
簡單證明:k ?(A + B) = k ? A + k ? B(這都還用證????不過出于數學邏輯思維的嚴謹,還是需要證明的)
兩個矩陣:



實現矩陣的基本運算
之前定義的向量類Vector:
import math
from ._globals import EPSILONclass Vector:def __init__(self, lst):self._values = list(lst)@classmethoddef zero(cls, dim):"""返回一個dim維的零向量"""return cls([0] * dim)def __add__(self, another):"""向量加法,返回結果向量"""assert len(self) == len(another), "Error in adding. Length of vectors must be same."return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量減法,返回結果向量"""assert len(self) == len(another), "Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""返回向量的單位向量"""if self.norm() < EPSILON:raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()def dot(self, another):"""向量點乘,返回結果標量"""assert len(self) == len(another), "Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def __mul__(self, k):"""返回數量乘法的結果向量:self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回數量乘法的結果向量:k * self"""return self * kdef __truediv__(self, k):"""返回數量除法的結果向量:self / k"""return (1 / k) * selfdef __pos__(self):"""返回向量取正的結果向量"""return 1 * selfdef __neg__(self):"""返回向量取負的結果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index個元素"""return self._values[index]def __len__(self):"""返回向量長度(有多少個元素)"""return len(self._values)def __repr__(self):return "Vector({})".format(self._values)def __str__(self):return "({})".format(", ".join(str(e) for e in self._values))
定義一個內部使用的文件_globals,用來存儲全局使用的變量 EPSILON,用來判斷精度用的

EPSILON = 1e-8定義的矩陣類Matrix:
from .Vector import Vectorclass Matrix:def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一個r行c列的零矩陣"""return cls([[0] * c for _ in range(r)])def __add__(self, another):"""返回兩個矩陣的加法結果"""assert self.shape() == another.shape(), "Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回兩個矩陣的減法結果"""assert self.shape() == another.shape(), "Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __mul__(self, k):"""返回矩陣的數量乘結果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩陣的數量乘結果: k * self"""return self * kdef __truediv__(self, k):"""返回數量除法的結果矩陣:self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩陣取正的結果"""return 1 * selfdef __neg__(self):"""返回矩陣取負的結果"""return -1 * selfdef row_vector(self, index):"""返回矩陣的第index個行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩陣的第index個列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩陣pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩陣的元素個數"""r, c = self.shape()return r * cdef row_num(self):"""返回矩陣的行數"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩陣的列數"""return self.shape()[1]def shape(self):"""返回矩陣的形狀: (行數, 列數)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__
測試代碼:
from playLA.Matrix import Matrixif __name__ == "__main__":matrix = Matrix([[1, 2], [3, 4]])print(matrix)print("matrix.shape = {}".format(matrix.shape()))print("matrix.size = {}".format(matrix.size()))print("len(matrix) = {}".format(len(matrix)))print("matrix[0][0] = {}".format(matrix[0, 0]))matrix2 = Matrix([[5, 6], [7, 8]])print(matrix2)print("add: {}".format(matrix + matrix2))print("subtract: {}".format(matrix - matrix2))print("scalar-mul: {}".format(2 * matrix))print("scalar-mul: {}".format(matrix * 2))print("zero_2_3: {}".format(Matrix.zero(2, 3)))



函數不能直接輸出string類型)



)
)









