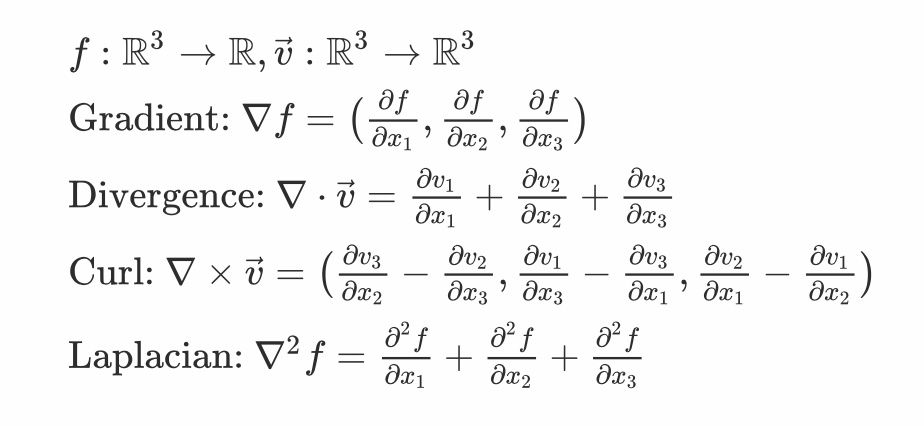
常微分方程（ODE） 的時候我們更多是關于時間的導數。偏微分方程（partial differential equation) 則不僅僅是與時間相關，加上了與空間位置相關的一些信息。

解

當 ODE 滿足 利普希茨連續（Lipschitz continuity），我們就可以有唯一解。但是 PDE 我們可能并沒有這樣好的性質，我們不知道它是否應該有解，很多時候也許我們就是用有限元方法（finite element method）來模擬，如果看到的結果還不錯的話，我們就當這個就是它的解，o(╯□╰)o

運算符

首先需要搞清楚： 梯度、散度、旋度、拉普拉斯 運算符:

關于 梯度、散度、旋度 以及 拉普拉斯可以理很久，如果需要復習，可以參見之前我寫過的兩篇：

• 梯度旋度散度
• 梯度、散度、旋度

在 物理 有關的偏微分方程中，如果函數是 f(t; x, y, z)， 當我們寫到 nabla 運算符是

,是與 t 無關的。

納維-斯托克斯方程 Navier-Stokes equations

Navier-Stokes equations 是大概做流體模擬的一個基礎方程，是一個典型的 PDE 方程：

或者我們用 wikipedia 中的寫法：

光看這個形式就很復雜了，是否可解這里光看式子就會想打上很多問號？？？所以克雷數學研究所的千禧年七大問題之一就是有關于 Navier-Stokes equations，

Prove or give a counter-example of the following statement:
In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier–Stokes equations.

價值 $1,000,000

其它的百萬問題還包括：

• P vs NP
• 霍奇猜想
• 龐加萊猜想
• 黎曼猜想
• ...

麥克斯韋方程組 Maxwell's equations

最最出名的 PDE 應該是 - 麥克斯韋方程組：

拉普拉斯方程 Laplace's equation

拉普拉斯方程非常出名， 形式簡單：

它是泊松方程的特殊形式。

拉普拉斯方程又被稱為調和方程。因為調和函數（harmonic function）的定義也就是函數滿足拉普拉斯方程。

之所以被定義為調和（harmonic）大概起因和 泛音(overtone)相關。

關于 調和函數 的另一種感性的理解就是如果我們把 拉普拉斯運算符 看成 類似二階導一樣的東西。

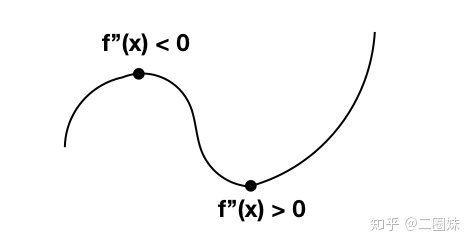
• 對于
  : 二階導 決定了這個函數的 凹凸性, 或者說 二階導 決定了這個點周圍的函數值是比它大還還是比它小。二階導 在這里變成了我們比較函數的與它鄰居的大小。

• 對于
  : 如果把它看成類似二階導，那么我們假設取一個點，然后看它周圍的圓（球，反正是與這個點距離相等的函數上的點），它們的平均值是跟這個點是一樣的。

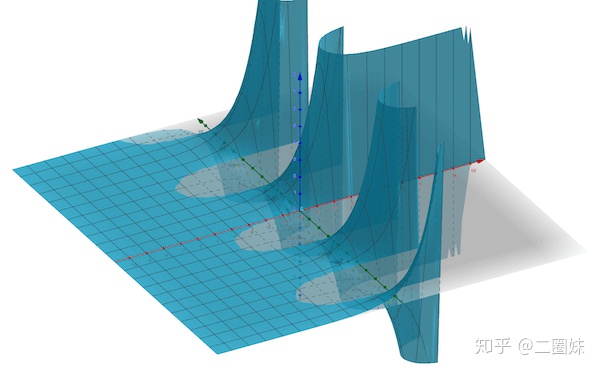
比如上面的 harmonic function:

， 雖然難以想象，但是比如我們在之上任意取一個點，這個點周圍的圓上面的函數值的平均是一樣的，在平坦的部分還容易想到這個結論，在有起伏的地方比較難想象到。

平均值一樣,某種意義上就代表穩定。

以下的兩個說法來自知乎問題： 調和函數到底有什么意義？

物理上可以用來描述一個穩定的狀態，比如定常的溫度場，自由電場電勢，引力勢能等等。數學上，比如說調和函數直接對應到復變里面的全純函數，微分幾何里面調和函數對應的是極小曲面，黎曼幾何里調和函數可以推廣到調和形式，然后就可以有Hodge 分解……上面每一個都可以展開，而且我強烈感覺我沒想全……簡直太有意義了
調和函數的線性組合仍為調和函數，所以是一個函數空間。調和函數無限次可導。調和函數在定義域的緊子集的邊界上達到最大最小值，這是一種類似單調的性質。加上其他的一些性質，導致調和函數容易處理也更可能滿足某些規律。以上是數學工作者看重的某些意義，你或許會覺得這不叫意義，那么可以考慮在物理學上的意義：二階偏導的和等于零，對應于加速度的和為零，即可以描述系統不受力的狀態，即穩態。當不能刻畫系統在每一時刻的狀態，卻能用調和函數描述系統穩態下的狀態，調和函數就顯得非常有意義了。

回頭繼續, 先扔一個問題的 setup：

也就是我們給定區域

， 它有邊界

，邊界上

有函數

，我們想要找到一個函數滿足

，也就是在這個邊界上相等。

那么

是在干什么呢？實際上這個函數有自己的名字 - 狄利克雷能量(Dirichlet's energy)：

這個 energy function 代表的是什么？

梯度代表的是 函數 的變化，類似于導數，這個一整個 梯度的 l2 norm的平方積分 - 導數變化求和，最小化 它 也就是最小化函數的變化。所以上面這個問題也就是在嘗試：

• 在邊界滿足 f = g
• 最小化函數 f 在區域內的變化

也就是讓函數盡量光滑，所以也就是 f 'as smooth as possible'.（ 記得之前還有過 'as rigid as possible')

可用變分解出，f 需要滿足 拉普拉斯方程。

考慮任意h，需要有：

考慮

關于

求導：

上述推導對于任何 h 都成立，特殊的，我們取

， 然后利用分布積分，其實也就是 格林恒等式：

上面式子可以轉化為：

這個式子恒等于0，所以也就是：

也就是我們需要求解的 PDE 為：

其實也就是 狄利克雷問題（Dirichlet problem）：

給定定義在

中一個區域的邊界上一個函數 g，是否存在惟一連續函數 f 在內部兩次連續可微，在邊界上連續，使得 f 在內部調和并在邊界上 f = g ？

其實這個也蠻像插值問題的，比如之前的插值， 給一些點，推斷出函數的模樣。維度升級了，給一個邊界，想要知道函數在區域內的全貌。

調和分析 Harmonic analysis

這也是一類PDE問題，解特征方程。

邊界條件 Boundary Value Problems

狄利克雷問題（Dirichlet problem）是給定邊界，推斷函數。類似的還包括：

• 狄利克雷邊界條件 Dirichlet conditions:
• 諾伊曼邊界條件 Neumann conditions:
• 混合 Robin boundary condition: 類似

二階PDE

二階PDE 的一般形式是：

我們也可以把上述方程寫成：

我們可以根據上面的式子來分類：

• A 是 正定矩陣 或者 負定矩陣 （特征值全為正或者全為負） ： 橢圓型 elliptic
• A 是 半正定矩陣 或者 半負定矩陣 （特征值除了全正或者全負，可以加上0）： 拋物型 parabolic
• A只存在一個特征值和其他特征值符號不同 ： 雙曲型 hyperbolic
• 不滿足上述條件 ： 超雙曲型 ultrahyperbolic

橢圓型 PDE

• 有解 & 唯一解
• 拉普拉斯/泊松方程

拋物型 PDE

• 短時間內的解是存在/唯一的
• 熱方程：
• 邊界條件 需要跟時間、空間相關

雙曲型 PDE

• 波動方程:
• 邊界條件: 一階導

微分看成算子

微分很容易驗證其為成線性算子。

先看一維簡單的例子，之前在數值積分和微分中已經討論過，比如我們可以用離散、差分等方式把

看成:

所以如果假設 f(x) 在 [0,1] 上有：

那么，這里就從微分到了差分，其實應該也 '≈' :

或者寫成：

如果我們把

寫成向量

， 把

寫成向量

，上面的式子可以寫成:

那么根據邊界條件的不同，

可以為：

Dirichlet

Neumann

然后我們就像解線性系統一樣來解這個系統了。

即使是 2D 的網格，我們也可以用類似的方法來離散：

感覺自己在有限元的邊緣試探，o(╯□╰)o

參考：

- 大量參考wikipedia