大數據HCIE成神之路之數據預處理（1）—

缺失值處理

- 1.1 刪除
- - 1.1.1 實驗任務
  - - 1.1.1.1 實驗背景
    - 1.1.1.2 實驗目標
    - 1.1.1.3 實驗數據解析
  - 1.1.2 實驗思路
  - 1.1.3 實驗操作步驟
  - 1.1.4 結果驗證
- 1.2 填充
- - 1.2.1 實驗任務
  - - 1.2.1.1 實驗背景
    - 1.2.1.2 實驗目標
    - 1.2.1.3 實驗數據解析
  - 1.2.2 實驗思路
  - 1.2.3 實驗操作步驟
  - 1.2.4 結果驗證
- 1.3 KNN
- - 1.3.1 實驗任務
  - - 1.3.1.1 實驗背景
    - 1.3.1.2 實驗目標
    - 1.3.1.3 實驗數據解析
  - 1.3.2 實驗思路
  - 1.3.3 實驗操作步驟
  - 1.3.4 結果驗證
- 1.4 回歸
- - 1.4.1 實驗任務
  - - 1.4.1.1 實驗背景
    - 1.4.1.2 實驗目標
    - 1.4.1.3 實驗數據解析
  - 1.4.2 實驗思路
  - 1.4.3 實驗操作步驟
  - 1.4.4 結果驗證

1.1 刪除

此方法適用于數據量大、數據缺失少的數據集。使用Python中pandas庫的dropna ( ) 函數，其基本格式如下：

DataFrame.dropna(axis=0, how='any', thresh=None, subset=None, inplace=False)

關鍵參數詳解：

axis=0/1，默認為0。axis=0代表行數據，axis=1代表列數據。
how=any/all，默認為any。how=any代表若某行或某列中存在缺失值，則刪除該行或該列。
how=all代表若某行或某列中數值全部為空，則刪除該行或該列。
thresh=N，可選參數，代表若某行或某列非缺失值的數量小于N，則刪除該行或該列。
subset=列名，可選參數，代表若指定列中有缺失值，則刪除該行。
inplace=True/False，Boolean數據, 默認為False。inplace=True代表直接對原數據集N做出修改。
inplace=False代表修改后生成新數據集M，原數據集N保持不變。

1.1.1 實驗任務

本課程將介紹基于Python的數據預處理方法，并針對常用預處理方法給出相應的具體編碼實現過程。通過學習本課程，學員將掌握基于Python的數據預處理方法，并能夠將其運用到實際項目中，解決業務問題。

1.1.1.1 實驗背景

利用Python對數據進行刪除操作，加深對dropna函數的理解。

1.1.1.2 實驗目標

設置dropna函數的各參數刪除缺失值。

1.1.1.3 實驗數據解析

本實驗章節—數據預處理，采用Python自帶的iris （鳶尾花）公有數據集進行操作。

鳶尾花數據集是以鳶尾花的特征作為數據來源，數據集包含150個數據記錄，分為3類，每類50個數據，每個數據包含4個特征屬性和1個目標屬性，共5維數據。

4個特征屬性的數值為浮點型數據，單位為厘米，分別是：

Sepal.Length（花萼長度）；
Sepal.Width（花萼寬度）；
Petal.Length（花瓣長度）；
Petal.Width（花瓣寬度））。

1個目標屬性為鳶尾花的類別，在數據集中以：0，1，2標識各類別。分別是：

Iris Setosa（山鳶尾）為0；
Iris Versicolour（雜色鳶尾）為1；
Iris Virginica（維吉尼亞鳶尾）為2。

原數據詳細信息如下：
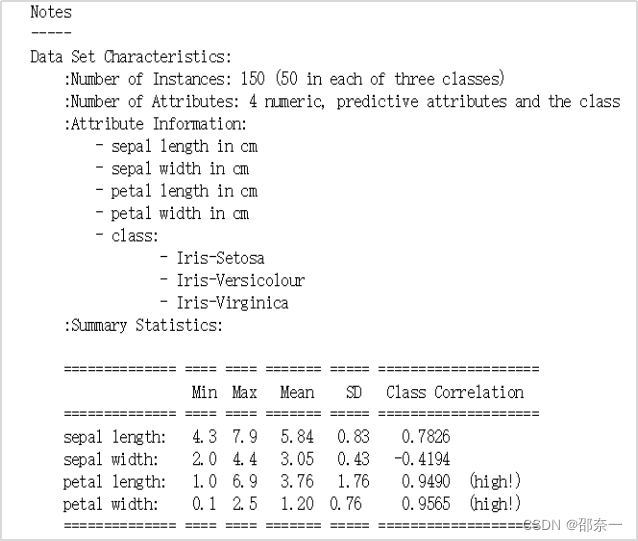
在這里插入圖片描述
部分原數據可視化后展示：

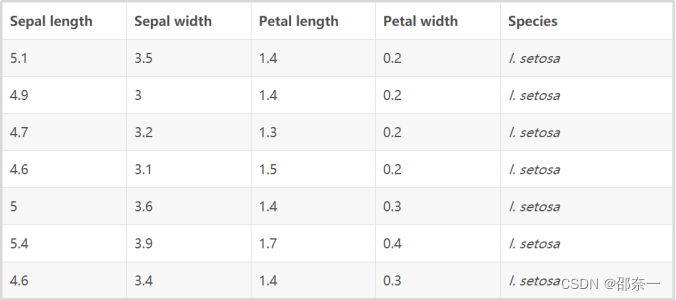
1.1.2 實驗思路

導入實驗數據集。
將數據集轉換成實驗要求的數據格式。
按照刪除條件，對數據集進行各類數據刪除操作。

1.1.3 實驗操作步驟

實驗一刪除數據集中的缺失值

步驟 1 數據準備

導入數據集 (大小為150*4)，屬性列分別為Sepal.Length (花萼長度), Sepal.Width (花萼寬度), Petal.Length (花瓣長度), Petal.Width (花瓣寬度)。

#導入pandas庫和numpy庫
import pandas as pd
import numpy as np
#導入數據集iris
from sklearn.datasets import load_iris
iris=load_iris()
#部分數據展示
iris

輸出結果如下：

{'data': array([[5.1, 3.5, 1.4, 0.2],[4.9, 3. , 1.4, 0.2],[4.7, 3.2, 1.3, 0.2],[4.6, 3.1, 1.5, 0.2],[5. , 3.6, 1.4, 0.2],[5.4, 3.9, 1.7, 0.4],[4.6, 3.4, 1.4, 0.3],[5. , 3.4, 1.5, 0.2],[4.4, 2.9, 1.4, 0.2],

說明：第一次執行后需要等待幾秒才會出來。

步驟 2 數據轉換

dropna() 函數適用于DataFrame結構的數據集，因此需先將iris數據集轉換成DataFrame結構，命名為dfx。DataFrame的參數data對應數據集iris.data，columns對應數據屬性iris.feature_names。

dfx=pd.DataFrame(data=iris.data, columns=iris.feature_names)

步驟 3 人為加入缺失值

因iris數據集中不含缺失值，因此需人為加入。

#創建名為c的缺失值數據集(名稱可自定義)，數據集中的屬性分別對應于iris中的4個屬性
#np.nan為Python中缺失值表示方式
c=pd.DataFrame({"sepal length (cm)":[np.nan,4.9],"sepal width (cm)":[np.nan,3],"petal length (cm)":[np.nan,1.4],"petal width (cm)":[0.2,np.nan]})
c

輸出結果如下：

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	        NaN	                NaN	                NaN	                 0.2
1	        4.9	                3.0	                1.4	                 NaN

使用append函數，將數據集c加入到iris數據集中，形成新數據集df。參數ignore_index為bool型，默認為False。

ignore_index設置為True。

df=dfx.append(c,ignore_index=True)
df

輸出結果如下：

#展示部分加入缺失值的數據集
149	5.9	3.0	5.1	1.8
150	NaN	NaN	NaN	0.2
151	4.9	3.0	1.4	NaN
152 rows × 4 columns

由上圖可看出，新加入了缺失值數據集。因ignore_index=True，所以兩組新數據的索引為150和151。

ignore_index設置為False。

df=dfx.append(c,ignore_index=False)
df

輸出結果如下：

#展示部分加入缺失值的數據集
149	5.9	3.0	5.1	1.8
0  	NaN	NaN	NaN	0.2
1  	4.9	3.0	1.4	NaN
152 rows × 4 columns

由上圖可看出，當ignore_index=False時，新加入數據的索引值保持原形式0和1。

解釋：

df=dfx.append(c,ignore_index=True)
#上面這種寫法已經過時，不建議使用，可以使用下面這種方式替換：
df=pd.concat([dfx,c],ignore_index=True)

步驟 4 刪除缺失值的多種形式展示

已知df數據集中行150和行151含有缺失值 (人為添加)，開始進行以下實驗：

刪除含缺失值NaN的數據行。結果如下：

df.dropna()
#關鍵結果展示
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
150 rows × 4 columns

df數據集中行150和行151已被刪除。

刪除含缺失值NaN的數據列。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(axis='columns')
0
1
2
3
4
5
6
……

因df數據集的4個屬性均含有缺失值NaN，因此df數據集完全被刪除。

刪除各屬性全為NaN的數據行。因數據集中無數據，則不刪除。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(how='all')

輸出結果如下：

#關鍵結果展示
149	5.9	3.0	5.1	1.8
150	NaN	NaN	NaN	0.2
151	4.9	3.0	1.4	NaN
152 rows × 4 columns

刪除存在缺失值NaN的數據行。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(how='any')

輸出結果如下：

#關鍵結果展示
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
150 rows × 4 columns

刪除數據行中非缺失值數量小于2（可自定義）的數據行。

df數據集中行150數值為[NaN,NaN,NaN,0.2]，只有一個數值是非缺失值，缺失值的數量小于2，應刪除此數據行。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(thresh=2)

輸出結果如下：

#關鍵結果展示
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
151	4.9	3.0	1.4	NaN
151 rows × 4 columns

刪除屬性列sepal width (cm)中含有缺失值NaN的數據行。

df數據集中只有行150中的sepal width (cm)為空，應刪除此數據行。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(subset=['sepal width (cm)'])

輸出結果如下：

#關鍵結果展示
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
151	4.9	3.0	1.4	NaN
151 rows × 4 columns

刪除含缺失值NaN的數據行，并生成新數據集。結果如下：

df=dfx.append(c,ignore_index=True)
df.dropna(inplace=False)

輸出結果如下：

#關鍵結果展示
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
150 rows × 4 columns

1.1.4 結果驗證

步驟四對數據集進行了多種情況下的刪除操作，由各自對應的輸出結果可以看出缺失值按照要求刪除。

刪除缺失值的操作比較多，總結如下方便記憶：

df=dfx.append(c,ignore_index=True)
df=pd.concat([dfx,c],ignore_index=True)
df.dropna(axis='columns')
df.dropna(how='all')
df.dropna(how='any')
df.dropna(thresh=2)
df.dropna(subset=['sepal width (cm)'])
df.dropna(inplace=False)

1.2 填充

填充包括定類-眾數填充 (Mode) 和定量-均值、中位數填充 (Mean, Median)。
Python的 sklearn.preprocessing 庫中的 Imputer 類可對缺失值進行眾數、均值、中位數填充。其基本格式如下：

Imputer(missing_values='NaN', strategy='mean', axis=0, verbose=0, copy=True)
fit_transform() #先擬合數據，再標準化

關鍵參數詳解：

missing_value，可選參數，int型或NaN，默認為NaN。這個參數定義了被視為缺失值的實際值。在這里，任何值為 ‘NaN’ 的數據都會被視為缺失值。
strategy =mean/median/most_frequent，可選參數，定義了用于替換缺失值的策略。
strategy=mean代表用某行或某列的 均值 填充缺失值。
strategy=median代表用某行或某列的 中位數值 填充缺失值。
strategy =most_frequent代表用某行或某列的 眾數 填充缺失值。
axis=0/1，默認為0，可選參數。axis=0代表行數據，axis=1代表列數據。一般實際應用中，axis取0。
verbose，默認為0，可選參數。控制Imputer的冗長。
copy=True/False， Boolean數據, 默認為True，可選參數。copy=True代表創建數據集的副本。

1.2.1 實驗任務

1.2.1.1 實驗背景

利用Python對數據進行填充操作，加深三種填充方法的理解。

1.2.1.2 實驗目標

使用均值、中位數、眾數填充缺失值。
此實驗中的數據集沿用實驗一中已添加缺失值的數據集df。

1.2.1.3 實驗數據解析

實驗數據直接使用鳶尾花數據集即可。

1.2.2 實驗思路

導入實驗數據集。
對數據集進行均值填充、中位數填充和眾數填充。

1.2.3 實驗操作步驟

實驗二使用填充方式處理數據集中的缺失值
步驟 1 數據準備

#導入pandas庫和numpy庫
import pandas as pd
import numpy as np
#導入數據集iris
from sklearn.datasets import load_iris
iris=load_iris()
dfx=pd.DataFrame(data=iris.data, columns=iris.feature_names)
c=pd.DataFrame({"sepal length (cm)":[np.nan,4.9],"sepal width (cm)":[np.nan,3],"petal length (cm)":[np.nan,1.4],"petal width (cm)":[0.2,np.nan]})#創建學生數據集,包含屬性列ID、weight和Height
df=dfx.append(c,ignore_index=True)
df

輸出結果如下：

147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8
150	NaN	NaN	NaN	0.2
151	4.9	3.0	1.4	NaN
152 rows × 4 columns

步驟 2 眾數填充
以未缺失數據的眾數來填充缺失值。紅色數據為眾數填充結果。

以下的運行結果只是展示，可不執行：

#導入Imputer類
from sklearn.preprocessing import Imputer
#使用Imputer函數進行缺失值填充，參數strategy設置為'most_frequent'代表用眾數填充
data = Imputer(missing_values='NaN', strategy='most_frequent', axis=0)
#對填充后的數據做歸一化操作
df=dfx.append(c,ignore_index=True)
dataMode = data.fit_transform(df)
#輸出dataMode
dataMode

上述代碼可能會報錯：

ImportError: cannot import name 'Imputer' from 'sklearn.preprocessing'

原因：Imputer類已在Scikit-learn 0.22版本中被棄用，Imputer不在preprocessing里了，而是在sklearn.impute里。而且改名成了SimpleImputer。

解決辦法：
第一步： from sklearn.impute import SimpleImputer
第二步：將程序中原來使用的 Imputer 改為 SimpleImputer
第三步： missing_values='NaN' 修改成： missing_values=np.nan

最終實現代碼如下：

from sklearn.impute import SimpleImputer
data = SimpleImputer(missing_values=np.nan, strategy='most_frequent')
# 對填充后的數據做歸一化操作
df = dfx.append(c, ignore_index=True)
dataMode = data.fit_transform(df)
# 輸出 dataMode
dataMode

輸出結果如下：

#關鍵結果展示[6.5, 3. , 5.2, 2. ],[6.2, 3.4, 5.4, 2.3],[5.9, 3. , 5.1, 1.8],[5. , 3. , 1.5, 0.2],[4.9, 3. , 1.4, 0.2]])

數據集df經Imputer函數處理后，變成numpy結構。如若想變成DataFrame結構，可進行如下操作。紅框部分為眾數填充結果。DataFrame內容可參考實驗手冊“Python語言基礎”中的“Pandas基本操作”部分。

mode=pd.DataFrame(data=dataMode,columns=['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)'])
mode

輸出結果如下：

#關鍵結果展示sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
149	   5.9	                 3.0	                5.1	               1.8
150	   5.0	                 3.0	                1.5	               0.2
151	   4.9	                 3.0	                1.4	               0.2

步驟 3 均值填充
以未缺失數據的均值來填充缺失值。紅色數據為均值填充結果。

舊版本代碼如下：

df=dfx.append(c,ignore_index=True)
data = Imputer(missing_values='NaN', strategy='mean', axis=0) 
dataMode = data.fit_transform(df)
dataMode

新版本代碼如下：

df=dfx.append(c,ignore_index=True)
data = SimpleImputer(missing_values=np.nan, strategy='mean') 
dataMode = data.fit_transform(df)
dataMode

輸出結果如下：

[6.5       , 3.        , 5.2       , 2.        ],[6.2       , 3.4       , 5.4       , 2.3       ],[5.9       , 3.        , 5.1       , 1.8       ],[5.83708609, 3.05364238, 3.74304636, 0.2   ],[4.9       , 3.        , 1.4       , 1.19205298]]

數據集df經Imputer函數處理后，變成numpy結構。如若想變成DataFrame結構，可按步驟二中的方法轉換，這里不再贅述。

步驟 4 中位數填充
以未缺失數據的中位數來填充缺失值。紅色數據為中位數填充結果。

舊版本代碼如下：

df=dfx.append(c,ignore_index=True)
data = Imputer(missing_values='NaN', strategy='median', axis=0)
dataMode = data.fit_transform(df)
dataMode

新版本代碼如下：

df=dfx.append(c,ignore_index=True)
data = SimpleImputer(missing_values=np.nan, strategy='median')
dataMode = data.fit_transform(df)
dataMode

輸出結果如下：

[6.5, 3. , 5.2, 2. ],[6.2, 3.4, 5.4, 2.3],[5.9, 3. , 5.1, 1.8],[5.8, 3. , 4.3, 0.2],[4.9, 3. , 1.4, 1.3]]

1.2.4 結果驗證

步驟二展示以 眾數 填充缺失值。經驗證，屬性值sepal length (cm) 的眾數是5.0，屬性值sepal width (cm) 的眾數是3.0，屬性值petal length (cm) 的眾數是2.0，屬性值petal width (cm) 的眾數是0.2。其結果和實驗結果一致。
步驟三展示以 均值 填充缺失值。經驗證，屬性值sepal length (cm) 的均值是5.83708609，屬性值sepal width (cm) 的均值是3.05364238，屬性值petal length (cm) 的均值是3.74304636，屬性值petal width (cm) 的均值是1.19205298。其結果和實驗結果一致。
步驟四展示以 中位數 填充缺失值。經驗證，屬性值sepal length (cm) 的中位數是5.8，屬性值sepal width (cm) 的中位數是3.0，屬性值petal length (cm) 的中位數是4.3，屬性值petal width (cm) 的中位數是1.3。其結果和實驗結果一致。

1.3 KNN

Python的 sklearn.neighbors 庫中的 KNeighborsClassifier 函數可預測缺失值，以便使用預測值填充數據。其基本格式如下：

KNeighborsClassifier(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, **kwargs)

關鍵參數詳解：

n_neighbors 可選參數，代表聚類數量，默認為5。
weights 可選參數，代表近鄰的權重值，uniform代表近鄰權重一樣，distance代表權重為距離的倒數，也可自定義函數確定權重，默認為 uniform 。
algorithm 可選參數，代表計算近鄰的算法，具體包括 {'auto', 'ball_tree', 'kd_tree', 'brute'} 。 auto 會根據傳遞給fit方法的值自動選擇最合適的算法。
leaf_size 可選參數，這是傳遞給樹的葉節點數量，代表構造樹的大小，默認為30。值一般選取默認值即可，太大會影響建模速度。
n_jobs 可選參數，代表數據計算的jobs數量，選取-1后雖然占據CPU比重會減小，但運行速度會變慢，所有的- core都會運行，默認為1。

可以忽略的參數：

p=2 ：這是Minkowski距離的冪參數。當p=1時，等同于使用 曼哈頓距離 ，當p=2時，等同于使用 歐幾里得距離 。
metric='minkowski' ：這是用于樹的距離度量。'minkowski’表示使用Minkowski距離。
metric_params=None ：這是度量函數的其他關鍵字參數。

說明： R語言在KNN填充缺失值方面更為完善和簡單，可用 DMwR 包中的

knnImputation(data, k = 10, scale = T, meth = "weighAvg", distData = NULL)

直接對缺失的自變量X進行缺失值填充。可參考如下鏈接學習：
R語言-缺失值處理1 - 銀河統計 - 博客園
KNN法處理缺失數據-Matlab-CSDN博客

1.3.1 實驗任務

1.3.1.1 實驗背景

利用KNN算法對數據集中的缺失值預測，加深此方法的理解。

1.3.1.2 實驗目標

使用KNN預測缺失值Y。測試數據如下，

“sepal length (cm)”:[5.6,4.9],
“sepal width (cm)”:[2.5,3],
“petal length (cm)”:[4.5,1.4],
“petal width (cm)”:[0.2,2.1]。

1.3.1.3 實驗數據解析

實驗數據同1.1.1.3。

1.3.2 實驗思路

導入實驗數據集。
生成實驗測試集。
利用實驗數據集進行KNN建模。
利用建好的KNN模型，對實驗測試集中的缺失值進行預測。

1.3.3 實驗操作步驟

實驗三使用KNN預測數據集中的缺失值

步驟 1 導入數據集

#導入pandas庫和numpy庫
import pandas as pd
import numpy as np
#導入數據集iris
from sklearn.datasets import load_iris
iris=load_iris()
# 導入iris數據集，自變量X命名為dfx，分類變量Y命名為dfy
dfx=pd.DataFrame(data=iris.data, columns=iris.feature_names)
dfx

輸出結果如下：

# 部分關鍵數據展示sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	       5.1	                3.5	                1.4	               0.2
1	       4.9	                3.0	                1.4	               0.2
2	       4.7	                3.2	                1.3	               0.2

繼續打印種類：

dfy=pd.DataFrame(data=iris.target)
dfy

輸出結果如下：

# 部分關鍵數據展示0
0	0
1	0
2	0
3	0
4	0
...	...
145	2
146	2
147	2
148	2
149	2

步驟 2 生成測試集

因iris無缺失值，因此手動生成不含分類變量的測試集x_test 。

x_test=pd.DataFrame({"sepal length (cm)":[5.6,4.9],"sepal width (cm)":[2.5,3],"petal length (cm)":[4.5,1.4],"petal width (cm)":[0.2,2.1]})
x_test

輸出結果如下：

sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	       5.6	                2.5	                4.5	               0.2
1	       4.9	                3.0	                1.4	               2.1

步驟 3 建模
基于iris數據集建立KNN模型。

# 導入KNeighborsClassifier
from sklearn.neighbors import KNeighborsClassifier
# KNN模型建立,將此數據集分為三簇，因此n_neighbors=3
modelKNN = KNeighborsClassifier(n_neighbors=3)
modelKNN.fit(dfx,dfy)

步驟 4預測

基于模型modelKNN，使用測試集x_test預測缺失值predicted。

# 預測
predicted = modelKNN.predict(x_test)
# 基于KNN模型，預測缺失值predicted
predicted

輸出結果為：

array([1, 0])

基于iris數據集建立的KNN模型預測缺失值Y分別為1和0。

缺失值預測的結果如下：

測試集				缺失值預測
sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	Y（預測結果）
5.6	2.5	4.5	0.2	1
4.9	3	1.4	2.1	0

1.3.4 結果驗證

經KNN模型預測，測試數據所屬類別為1和0。說明在iris數據集中，距離測試數據1最近的點屬于類別1，距離測試數據2最近的點屬于類別0。

1.4 回歸

此方式只適用于缺失值是連續的情況，比如，北京二手房價缺失值填充。因此上述iris數據集不適用于此方法預測缺失值。

Python的 sklearn.linear_model 庫中的 LinearRegression 函數可進行回歸預測，以便進行數據填充。其基本格式如下：

model = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

關鍵參數詳解：

fit_intercept=True/Flase，Boolean數據，默認為True，可選參數。fit_intercept =True代表建模是考慮截距。- fit_intercept=Flase代表建模時不考慮截距。
normalize=True/Flase，Boolean數據, 默認為Flase，可選參數。fit_intercept=Flase代表忽略normalize參數。fit_intercept =True且normalize=True代表回歸之前要對自變量X進行歸一化。
copy_X=True/False，Boolean，默認為True，可選參數。copy_X=True代表自變量可以被copy，否則，它將被重寫。
n_jobs，默認為1，可選參數。

思考：“fit_intercept =True且normalize=True代表回歸之前要對自變量X進行歸一化。”是什么意思？

當fit_intercept=True且normalize=True時，表示在執行線性回歸之前，會對自變量X進行歸一化處理。歸一化是指將數據按比例縮放，使之落入一個小的特定區間。在數學上，這種無量綱化可以在一定程度上消除數據量綱和取值范圍的影響，使得不同指標之間具有可比性。

例如，假設我們有以下數據：

X = [[1, 200], [2, 300], [3, 400]]
y = [1, 2, 3]

在這個例子中，X的第二個特征的值遠大于第一個特征的值。如果我們直接進行線性回歸，可能會導致第二個特征對模型的影響過大。為了解決這個問題，我們可以對X進行歸一化處理，使得所有特征的值都在0到1之間。這樣，所有特征對模型的影響就相對均衡了。

歸一化的公式如下：

$X_{\text{norm}} = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}}$

其中， $X_{\text{min}}$ 和 $X_{\text{max}}$ 分別是X的最小值和最大值。

好的，現在可以按照以下步驟對數據進行歸一化處理：

首先，我們需要找到每個特征的最小值和最大值。在這個例子中，第一個特征的最小值是1，最大值是3；第二個特征的最小值是200，最大值是400。
然后，我們將每個特征的值減去該特征的最小值，然后除以該特征的最大值和最小值的差。這樣，每個特征的值都會在0到1之間。

具體計算如下：

X_norm = [[(1-1)/(3-1), (200-200)/(400-200)],  # 第一個樣本[(2-1)/(3-1), (300-200)/(400-200)],  # 第二個樣本[(3-1)/(3-1), (400-200)/(400-200)]]  # 第三個樣本

所以，歸一化后的數據為：

X_norm = [[0.0, 0.0],[0.5, 0.5],[1.0, 1.0]]

這樣，所有特征的值都在0到1之間，每個特征對模型的影響相對均衡。希望這個解釋對你有所幫助！

所以，當fit_intercept=True且normalize=True時，LinearRegression會自動對X進行歸一化處理，然后再進行線性回歸。這樣可以確保所有特征對模型的影響是均衡的。

1.4.1 實驗任務

1.4.1.1 實驗背景

利用回歸算法對數據集中的缺失值預測，加深此方法的理解。

1.4.1.2 實驗目標

使用回歸模型預測缺失值。假設屬性Weight (自變量) 和屬性Height(因變量)有關，因此可根據Weight和Height建立回歸模型，進而預測缺失值Height。

1.4.1.3 實驗數據解析

學生數據集sInfo，屬性列為ID、Weight和Height。

回歸實驗數據如下：

序號	01	02	03	04	05	06	07	08	09	10
ID	001	002	003	004	005	006	007	008	009	010
Weight	55	54	51	45	67	68	67	55	54	56
Height	NA	165	NA	160	170	168	167	162	169	166

1.4.2 實驗思路

導入實驗數據集。
刪除缺失值。
利用不含缺失值的實驗數據集進行回歸建模。
基于建好的回歸模型，用數據集中含缺失值的數據列預測其中的缺失值。

1.4.3 實驗操作步驟

實驗四使用回歸預測數據集中的缺失值

步驟 1 導入數據

# 創建學生數據集sInfo，屬性列為ID、Weight和Height
import pandas as pd
import numpy as np
sInfo=pd.DataFrame({"ID":['001','002','003','004','005','006','007','008',
'009','010'],"Weight":['55','54','51','45','67','68','67','55','54','56'], "Height":[np.nan,'165',np.nan,'160','170','168','167','162','169','166']})
# 查看數據
sInfo

輸出結果如下：

	ID	Weight	Height
0	001	55	NaN
1	002	54	165
2	003	51	NaN
3	004	45	160
4	005	67	170
5	006	68	168
6	007	67	167
7	008	55	162
8	009	54	169
9	010	56	166

觀察數據集sInfo可知，sInfo中缺失Height數據。

步驟2 刪除缺失值

用 dropna() 刪除數據集中的缺失值。

# dropna函數中參數how設置為any，代表刪除數據中存在NaN的行數據。參數inplace設置為False，代表生成新的數據集sInfonew (dropna函數的詳細見2.2.1.1)。
sInfonew=sInfo.dropna(how='any',inplace=False)
sInfonew

輸出結果如下：

	ID	Weight	Height
1	002	54	165
3	004	45	160
4	005	67	170
5	006	68	168
6	007	67	167
7	008	55	162
8	009	54	169
9	010	56	166

可以發現ID為001跟003的這兩行身高是空的行已經被刪掉了。

步驟3 建立回歸模型

基于現有數據建立回歸模型，新版本Python要求對數據使用 values.reshape( ) ，確保訓練數據維度和模型要求一致。

# 基于兩個變量建立回歸模型。
from sklearn.linear_model import LinearRegression
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(sInfonew['Weight'].values.reshape(-1,1),sInfonew['Height'].values. reshape(-1,1))

解釋：

model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)：這行代碼創建了一個LinearRegression對象，并將其賦值給變量model。這個對象將用于擬合線性回歸模型。參數的含義如下：
- copy_X=True：這意味著在進行計算之前，會對輸入數據X進行復制。這樣可以避免對原始數據進行更改。
- fit_intercept=True：這意味著模型將包含截距項。如果設置為False，則認為數據已經居中，不會計算截距項。
- n_jobs=1：這是用于計算的CPU核心數量。1表示只使用一個核心。
- normalize=False：這意味著在進行回歸之前，不會對輸入數據X進行歸一化處理。如果設置為True，則會對X進行歸一化。
model.fit(sInfonew['Weight'].values.reshape(-1,1),sInfonew['Height'].values. reshape(-1,1))：這行代碼是用來擬合線性回歸模型的。fit方法接受兩個參數：X和y，分別代表特征和目標變量。在這個例子中，我們使用Weight作為特征，Height作為目標變量。reshape(-1,1)是用來確保數據的形狀正確，-1表示行數由數據的大小決定，1表示列數為1。

思考： n_jobs 此參數應該是多少比較合適？此參數的調整與什么相關？

n_jobs參數決定了在進行模型訓練時，計算機用于并行計算的CPU核心數量。這個參數的設定與以下因素相關：

計算機的硬件配置：如果你的計算機有多個CPU核心，那么可以設置n_jobs為一個大于1的整數，以利用多核并行計算的優勢，加快模型訓練的速度。如果你的計算機只有一個CPU核心，那么n_jobs應該設置為1。
模型訓練的復雜性：如果你的模型訓練任務非常復雜，需要大量的計算資源，那么可以考慮設置n_jobs為一個較大的值，以提高計算效率。但是，如果你的模型訓練任務相對簡單，那么即使設置n_jobs為一個較大的值，也可能無法顯著提高訓練速度。
其他任務的需求：如果你的計算機同時還需要處理其他任務，那么可能需要考慮將n_jobs設置為一個較小的值，以避免占用過多的CPU資源。

值得注意的是，如果你將n_jobs設置為-1，那么sklearn會使用所有可用的CPU核心進行計算。總的來說，n_jobs的設定需要根據你的具體情況進行權衡。

步驟4 基于回歸模型預測缺失值

使用構建完成的model預測Height。

# 當Weight為55時，使用模型預測對應Height
y1 = model.predict([[55]])
# y1預測結果
y1

輸出結果如下：

array([[164.86855941]])

預測y2對應的Height值。

# 當Weight為51時，使用模型預測對應Height
y2 = model.predict([[51]])
# y2預測結果
y2

輸出結果如下：

array([[163.6298633]])

同時預測Weight為55和51的Height值，代碼如下：

# 當Weight為55和51時，使用模型預測對應Height
y3 = model.predict([[55],[51]])
# y3預測結果
y3

輸出結果如下：

array([[164.86855941],[163.6298633 ]])

1.4.4 結果驗證

根據model預測出當Weight為 55 時，Height為 164.86855941 。當Weight為 51 時，Height為 163.6298633 。