本系列側重于例題實戰與講解，希望能夠在例題中理解相應技巧。文章開頭相關基礎知識只是進行簡單回顧，讀者可以搭配課本或其他博客了解相應章節，然后進入本文例題實戰，效果更佳。

如果這篇文章對你有幫助，歡迎點贊與收藏~

回歸分析基本概念

在當今數據驅動的研究與決策制定中，回歸分析扮演著至關重要的角色。它是一種統計方法，用于研究和建模兩組或多組變量之間的關系。在實際問題中，特別是當我們面臨著大量相關的自變量（預測變量）和因變量（響應變量）時，選擇合適的回歸分析方法變得尤為重要。

經典多元線性回歸（MLR）

多元線性回歸是最基本且廣泛使用的回歸分析形式。它旨在使用多個預測變量來預測一個因變量。基于最小二乘準則，它通過最小化預測值和實際值之間的平方差來找到最佳擬合線。然而，當變量間存在多重共線性，或者自變量的數量遠大于觀測樣本量時，多元線性回歸的效果可能會受到限制。

主成分回歸（PCR）

為了解決多元回歸中的多重共線性問題，主成分回歸（PCR）技術被提出。PCR先對自變量進行主成分分析（PCA），以減少變量間的共線性，并提取少量的主成分。然后，這些主成分被用作新的預測變量在回歸分析中。這種方法有效降低了變量間的依賴性，但可能會丟失對原始變量的直接解釋性。

偏最小二乘回歸（PLS）

偏最小二乘回歸是一種先進的多對多線性回歸建模方法。它特別適用于自變量和因變量都很多、彼此間存在多重相關性，而樣本量又相對較少的情況。PLS不僅考慮了自變量間的關系，還考慮了自變量與因變量間的關系。它通過尋找兩組變量中共同變異的方向，可以在減少數據維度的同時，保留對響應變量有用的信息。

建模過程

PLS回歸在建模時綜合了主成分分析、典型相關分析和線性回歸分析的特點。它不僅提供了一個合理的回歸模型，而且還能進行類似于主成分分析和典型相關分析的探索，提供更豐富和深入的信息。

應用和優勢

PLS回歸在許多領域都有應用，特別是在化學計量學、生物信息學和社會科學中。它的優勢在于能夠處理高維數據集，解決多重共線性問題，并提供對復雜數據結構的深入理解。

偏最小二乘回歸分析概述

偏最小二乘回歸（PLS回歸）分析是一種統計方法，它在多元統計分析中被用來建立因變量和自變量之間的線性關系模型。它是一種在因變量和自變量之間建立最大協方差的模型，尤其適合于變量個數多于觀測數，或者變量之間存在多重共線性的情況。PLS回歸不僅能夠處理多維數據集，而且還能夠在減少變量時保持模型的預測能力。

PLS回歸的基本思想是將原始的自變量矩陣和因變量矩陣分別投影到新的空間，這些新空間的基是由原始變量的線性組合構成的。這些新空間的基被稱為潛在變量或PLS成分。通過這種方式，PLS回歸旨在找到少數幾個潛在變量，這些潛在變量能夠最好地解釋自變量和因變量之間的關系。

PLS回歸分析的步驟通常包括以下幾個關鍵階段：

1. 算法初始化：選擇初始權重，開始迭代過程。
2. 權重向量的計算：計算自變量和因變量的權重向量，這些權重向量定義了原始變量到潛在變量空間的映射。
3. 潛在變量的提取：用權重向量提取自變量和因變量的得分，這些得分代表了潛在變量。
4. 內部關系的建立：在潛在變量空間內，建立自變量得分和因變量得分之間的回歸模型。
5. 模型優化：通過交叉驗證等方法確定潛在變量的最佳數目，以避免過擬合。
6. 參數估計：在確定了潛在變量數目后，用所有數據重新估計PLS回歸模型的參數。
7. 模型評估：使用一些統計標準，如預測殘差平方和（PRESS）和決定系數（R2），來評價模型的預測能力和解釋能力。

習題11.1

1. 題目要求

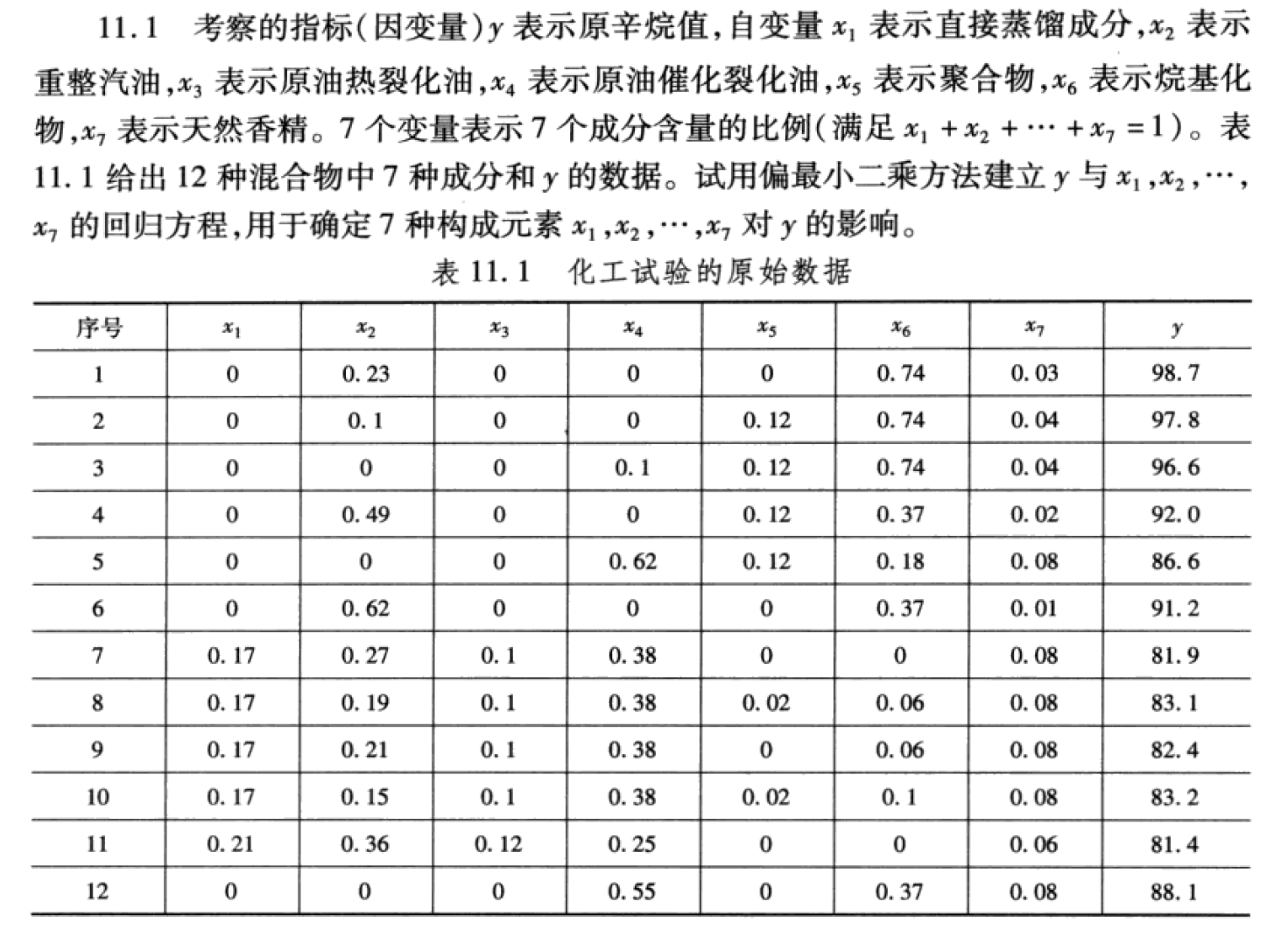
2.解題過程

解：

12個樣本點分別用 i=1,…,12 表示各個樣本點，自變量的觀測數據矩陣即為$A=(a_{ij}{)}_{12\times 7}$，因變量的觀測數據矩陣即為$B=[b_1,...,b_{12}{]}^T$。

（1）

數據標準化

將各指標值$a_{ij}$轉換成標準化指標值$\widetilde{a_{ij}}$，即
$$\widetilde{a_{ij}}=\frac{a_{ij}?{\mu }_j^{(1)}}{s_j^{(1)}},i=1,2,...,12,j=1,...,7.$$
式中：
$$\begin{gathered} {\mu }_j^{(1)}=\frac{1}{12}\sum _{i=1}^{12}{a}_{ij}, \\ {s}_j^{(1)}=\sqrt{\frac{1}{12?1}\sum _{i=1}^{12}(a_{ij}?{\mu }_j^{(1)}{)}^2},(j=1,...,7), \end{gathered}$$
即${\mu }_j^{(1)}$、$s_j^{(1)}$為第j個自變量$x_j$的樣本均值和樣本標準差。對應地，稱
$$\widetilde{x_j}=\frac{x_j?{\mu }_j^{(1)}}{s_j^{(1)}},j=1,...,7.$$
為標準化指標變量。

類似地，將$b_i$轉換成標準化指標值$\widetilde{b_i}$，即
$$b_i=\frac{b_i?{\mu }^{(2)}}{s^{(2)}},i=1,2,...,12,$$
式中：
$$\begin{gathered} {\mu }^{(2)}=\frac{1}{12}\sum _{i=1}^{12}{b}_i \\ {s}^{(2)}=\sqrt{\frac{1}{12?1}\sum _{i=1}^{12}(b_i?{\mu }^{(2)}{)}^2} \end{gathered}$$
即${\mu }^{(2)},s^{(2)}$為因變量y的樣本均值和樣本標準差；

對應地，稱
$$\tilde{y}=\frac{y?{\mu }^{(2)}}{s^{(2)}}$$
為對應的標準化變量。

（2）

分別提出自變量組和因變量組的成分。使用matlab求得7對成分，其中第一對成分為
$$\begin{array}{c}\{\begin{array}{ll}{\mu }_1& =?0.0906\widetilde{x_1}?0.0575{\tilde{x}}_2?0.0804{\tilde{x}}_3?0.116{\tilde{x}}_4+0.0238{\tilde{x}}_5?0.0657{\tilde{x}}_7,\\ v_1& =3.1874{\tilde{y}}_1.\end{array}\end{array}$$
前三個成分解釋自變量的比率為91.83%，只要取3對成分即可。

（3）

求三個成分對標準化指標變量與成分變量之間的回歸方程，求得自變量組和因變量組與$u_1、u_2、u_3$之間的回歸方程分別為：

$${\tilde{x}}_1=?2.9991u_1?0.1186u_2+1.0472u_3,$$

$${\tilde{x}}_2=0.2095u_1?2.7981u_2+1.7237u_3,$$

…

$${\tilde{x}}_7=?2.7279u_1+1.3298u_2?1.3002u_3,$$

$${\tilde{y}}_1=3.1874u_1+0.7617u_2+0.3954u_3,$$

（4）

求因變量組與自變量組之間的回歸方程

把（2）中成分$u_i$代入（3）中的回歸方程，得到標準化指標變量的回歸方程為：
$${\tilde{y}}_1=?0.1391{\tilde{x}}_1?0.2087{\tilde{x}}_2?0.1376{\tilde{x}}_3?0.2932{\tilde{x}}_4?0.0384{\tilde{x}}_5+0.4564{\tilde{x}}_6?0.1434{\tilde{x}}_7.$$
將標準化變量$\tilde{y},{\tilde{x}}_j,(j=1,...,7)$分別還原成原始變量$y,x_j$，就可以得到結果。

3.程序

求解的MATLAB程序如下：

clc, clear% 導入數據
ab0 = [0, 0.23, 0, 0, 0, 0.74, 0.03, 98.7; ...0, 0.1, 0, 0, 0.12, 0.74, 0.04, 97.8; ...0, 0, 0, 0.1, 0.12, 0.74, 0.04, 96.6; ...0, 0.49, 0, 0, 0.12, 0.37, 0.02, 92.0; ...0, 0, 0, 0.62, 0.12, 0.18, 0.08, 86.6; ...0, 0.62, 0, 0, 0, 0.37, 0.01, 91.2; ...0.17, 0.27, 0.1, 0.38, 0, 0, 0.08, 81.9; ...0.17, 0.19, 0.1, 0.38, 0.02, 0.06, 0.08, 83.1; ...0.17, 0.21, 0.1, 0.38, 0, 0.06, 0.08, 82.4; ...0.17, 0.15, 0.1, 0.38, 0.02, 0.1, 0.08, 83.2; ...0.21, 0.36, 0.12, 0.25, 0, 0, 0.06, 81.4; ...0, 0, 0, 0.55, 0, 0.37, 0.08, 88.1];
% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 標準化以后的自變量和因變量數據
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);% 主成分的個數3
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 3);n = size(a, 2);
m = size(b, 2);format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)%直方圖
bar(BETA','k');

4.結果

所以，最終建立的回歸方程如下：
$$\begin{array}{rl}y& =92.6759894798203?9.82831779652421\times x_1?6.96018146108128\times x_2?16.6662390524996\times x_3\\ & ?8.4218024072797\times x_4?4.38893380525098\times x_5+10.1613044805558\times x_6\\ & ?34.5289588223774\times x_7\end{array}$$

習題11.2

1. 題目要求

2.解題過程

解：

解題思路與方法與上一題類似，本題不再詳細贅述。

不同點在于，本題一共有5對成分。

3.程序

求解的MATLAB程序如下：

clc, clear% 導入數據
ab0 = [46, 55, 126, 51, 75.0, 25, 72, 6.8, 489, 27, 8, 360; ...52, 55, 95, 42, 81.2, 18, 50, 7.2, 464, 30, 5, 348; ...46, 69, 107, 38, 98.0, 18, 74, 6.8, 430, 32, 9, 386; ...49, 50, 105, 48, 97.6, 16, 60, 6.8, 362, 26, 6, 331; ...42, 55, 90, 46, 66.5, 2, 68, 7.2, 453, 23, 11, 391; ...48, 61, 106, 43, 78.0, 25, 58, 7.0, 405, 29, 7, 389; ...49, 60, 100, 49, 90.6, 15, 60, 7.0, 420, 21, 10, 379; ...48, 63, 122, 52, 56.0, 17, 68, 7.0, 466, 28, 2, 362; ...45, 55, 105, 48, 76.0, 15, 61, 6.8, 415, 24, 6, 386; ...48, 64, 120, 38, 60.2, 20, 62, 7.0, 413, 28, 7, 398; ...49, 52, 100, 42, 53.4, 6, 42, 7.4, 404, 23, 6, 400; ...47, 62, 100, 34, 61.2, 10, 62, 7.2, 427, 25, 7, 407; ...41, 51, 101, 53, 62.4, 5, 60, 8.0, 372, 25, 3, 409; ...52, 55, 125, 43, 86.3, 5, 62, 6.8, 496, 30, 10, 350; ...45, 52, 94, 50, 51.4, 20, 65, 7.6, 394, 24, 3, 399; ...49, 57, 110, 47, 72.3, 19, 45, 7.0, 446, 30, 11, 337; ...53, 65, 112, 47, 90.4, 15, 75, 6.6, 420, 30, 12, 357; ...47, 57, 95, 47, 72.3, 9, 64, 6.6, 447, 25, 4, 447; ...48, 60, 120, 47, 86.4, 12, 62, 6.8, 398, 28, 11, 381; ...49, 55, 113, 41, 84.1, 15, 60, 7.0, 398, 27, 4, 387; ...48, 69, 128, 42, 47.9, 20, 63, 7.0, 485, 30, 7, 350; ...42, 57, 122, 46, 54.2, 15, 63, 7.2, 400, 28, 6, 388; ...54, 64, 155, 51, 71.4, 19, 61, 6.9, 511, 33, 12, 298; ...53, 63, 120, 42, 56.6, 8, 53, 7.5, 430, 29, 4, 353; ...42, 71, 138, 44, 65.2, 17, 55, 7.0, 487, 29, 9, 370; ...46, 66, 120, 45, 62.2, 22, 68, 7.4, 470, 28, 7, 360; ...45, 56, 91, 29, 66.2, 18, 51, 7.9, 380, 26, 5, 358; ...50, 60, 120, 42, 56.6, 8, 57, 6.8, 460, 32, 5, 348; ...42, 51, 126, 50, 50.0, 13, 57, 7.7, 398, 27, 2, 383; ...48, 50, 115, 41, 52.9, 6, 39, 7.4, 415, 28, 6, 314; ...42, 52, 140, 48, 56.3, 15, 60, 6.9, 470, 27, 11, 348; ...48, 67, 105, 39, 69.2, 23, 60, 7.6, 450, 28, 10, 326; ...49, 74, 151, 49, 54.2, 20, 58, 7.0, 500, 30, 12, 330; ...47, 55, 113, 40, 71.4, 19, 64, 7.6, 410, 29, 7, 331; ...49, 74, 120, 53, 54.5, 22, 59, 6.9, 500, 33, 21, 348; ...44, 52, 110, 37, 54.9, 14, 57, 7.5, 400, 29, 2, 421; ...52, 66, 130, 47, 45.9, 14, 45, 6.8, 505, 28, 11, 355; ...48, 68, 100, 45, 53.6, 23, 70, 7.2, 522, 28, 9, 352];% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 標準化以后的自變量和因變量數據
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);% 主成分個數5
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 5);n = size(a, 2);
m = size(b, 2);format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)%直方圖
bar(BETA', 'k');

4.結果

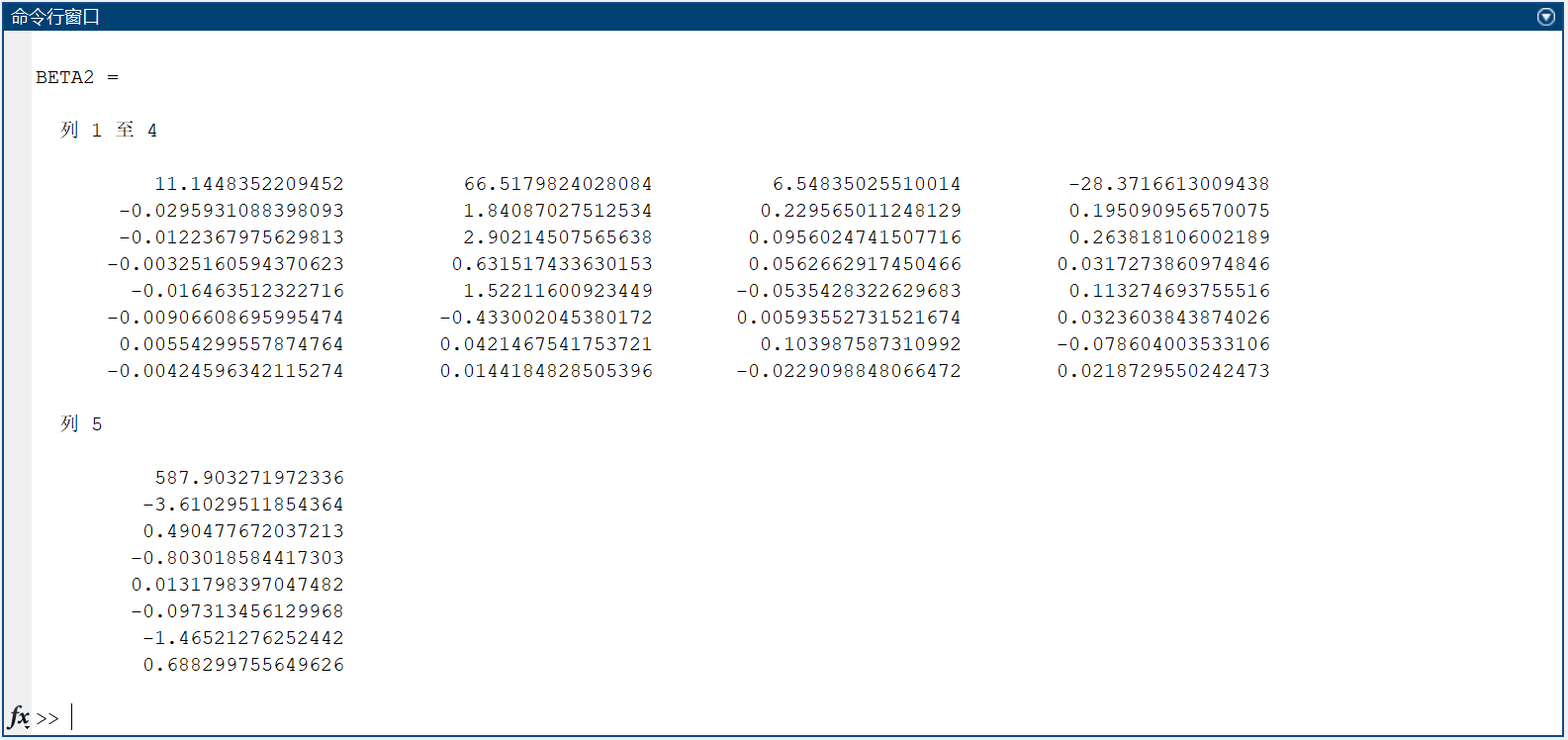
所以，最終建立的回歸方程如下：
$$\begin{array}{rl}{y}_1& =11.1448352209452?0.0295931088398093\times x_1?0.0122367975629813\times x_2?0.00325160594370623\times x_3\\ & ?0.016463512322716\times x_4?0.00906608695995474\times x_5+0.00554299557874764\times x_6\\ & ?0.00424596342115274\times x_7\\ y_2& =66.5179824028084+1.84087027512534\times x_1+2.90214507565638\times x_2+0.631517433630153\times x_3\\ & +1.52211600923449\times x_4?0.433002045380172\times x_5+0.0421467541753721\times x_6\\ & +0.0144184828505396\times x_7\\ y_3& =6.54835025510014+0.229565011248129\times x_1+0.0956024741507716\times x_2+0.0562662917450466\times x_3\\ & ?0.0535428322629683\times x_4+0.00593552731521674\times x_5+0.103987587310992\times x_6\\ & ?0.0229098848066472\times x_7\\ y_4& =?28.3716613009438+0.195090956570075\times x_1+0.263818106002189\times x_2+0.0317273860974846\times x_3\\ & +0.113274693755516\times x_4+0.0323603843874026\times x_5?0.078604003533106\times x_6\\ & +0.0218729550242473\times x_7\\ y_5& =587.903271972336?3.61029511854364\times x_1+0.490477672037213\times x_2?0.803018584417303\times x_3\\ & +0.0131798397047482\times x_4?0.097313456129968\times x_5?1.46521276252442\times x_6\\ & +0.688299755649626\times x_7\end{array}$$

如果這篇文章對你有幫助，歡迎點贊與收藏~