
一、說明
????????在這篇文章,我將向您解釋集成技術和著名的集成技術之一,它屬于裝袋技術,稱為隨機森林分類器和回歸。
????????集成技術是機器學習技術,它結合多個基本模塊和模型來創建最佳預測模型。為了更好地理解這個定義,我們需要退一步考慮機器學習和模型構建的最終目標。一旦我們對此有了清晰的認識,我們就可以深入研究具體的例子以及首選集成模型的原因。在上一篇文章中,我們學習了決策樹。
機器學習算法(8)——決策樹算法
在本文中,我將重點討論決策樹的用途。決策樹是最強大的之一......
向開發網
????????本文討論使用決策樹來確定個人是否應該在某些天氣條件下在戶外打高爾夫球。這棵樹會考慮各種天氣因素,并根據每個因素做出決定或提出另一個問題。例如,如果是陰天,則決定在外面玩,但如果是晴天、雨天或有風,樹會在決定是否玩之前詢問進一步的問題。
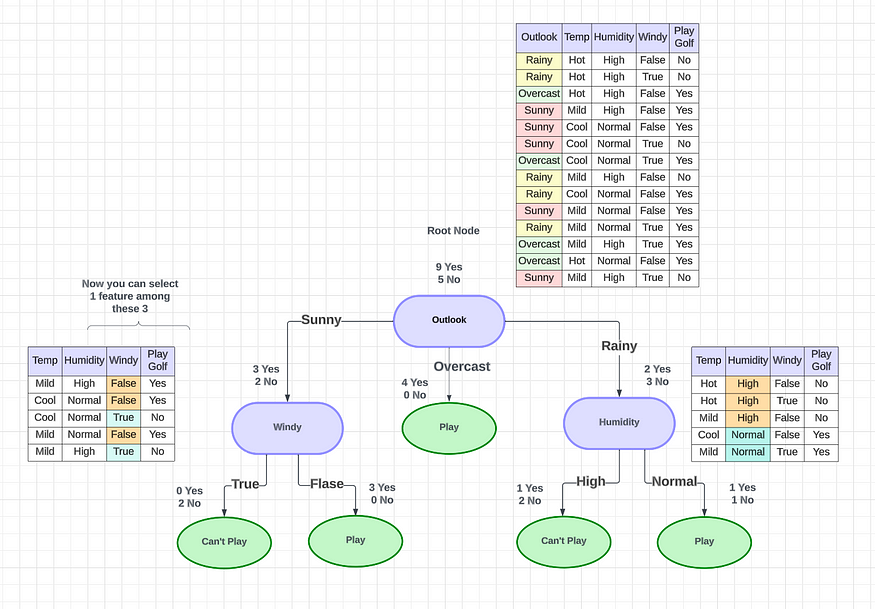
????????要創建決策樹,我們必須考慮將使用哪些特征來做出決策,以及將使用什么閾值將每個問題分類為是或否答案。我們可以繼續添加問題,直到定義是和否類。但如果我們想問自己是否有朋友可以一起玩,會發生什么呢?如果我們有朋友的話,我們每次都會玩。如果沒有,我們可能會繼續問自己有關天氣的問題。通過添加一個附加問題,我們希望更好地定義“是”和“否”類。但我們怎樣才能做到這一點呢?
????????這里需要用到集成技術。使用集成方法使我們能夠考慮決策樹樣本,確定每次分割時使用哪些特征,并根據樣本決策樹的聚合結果做出最終預測器。這種方法比僅依靠一棵決策樹來做出最終決策更可靠。在 Esemble 技術中,有 2 種技術。
- 套袋技術
- 升壓技術
二、裝袋技術如何發揮作用?
????????Bagging 也稱為引導聚合,通過使用多個模型訓練數據集來獲得更準確的輸出。這個主題特別重要,因為許多公司現在在數據分析中使用這些技術。
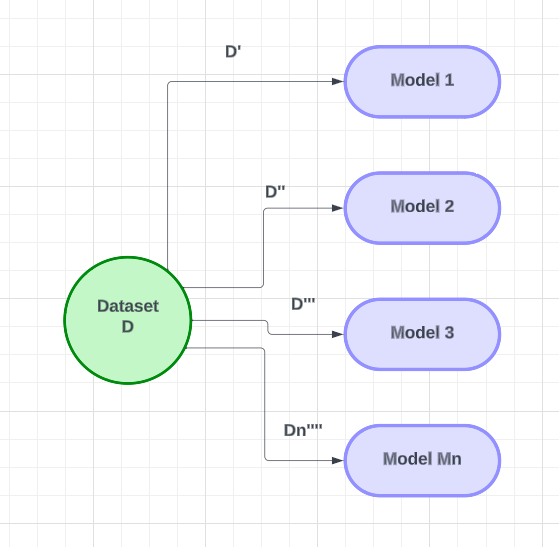
????????假設我們有一個特定的問題陳述,并且有一個名為 D 的數據集。在這個特定的數據集中,我們將創建幾個基本模型(M1、M2、M3 …… Mn)并使用它們來創建基于多個的學習器。對于每個模型,我們將向M1 模型提供小于數據集中記錄數(n)的數據集樣本(D')。我們將使用行采樣和每個模型的替換來提供數據。對于下一個模型,我們將重復相同的過程,我們將重新采樣記錄并將其提供給模型。每個模型都會有一組不同的數據。在向模型提供數據后,他們將接受數據訓練。將對組中的所有模型重復此過程。

完成訓練后,我們將使用測試數據集中的新數據進行預測。對于二元分類,我們將“測試 D”數據發送到模型 1。如果模型1輸出1,模型2輸出0,模型3輸出1,模型Mn輸出1,我們將使用投票分類器來組合測試數據的模型的輸出(為1)。獲得多數票的輸出將被考慮。通過使用帶替換的行采樣和投票分類器,我們將組合模型的輸出以獲得最終結果。這就是套袋技術的工作原理。
注意:對于回歸問題,我們可以將輸出均值作為最終結果。
在裝袋技術中,我們使用兩種算法,
- 隨機森林分類器
- 隨機森林回歸
三、隨機森林分類器和隨機森林回歸

????????自舉隨機森林算法將集成學習方法與決策樹框架相結合,從數據中創建多個隨機抽取的決策樹,對結果進行平均以輸出新結果,這通常會導致強大的預測/分類。
????????讓我向您展示一些示例,以幫助您了解隨機如何處理數據集。在bagging中,我們使用多個基學習器模型,例如決策樹1、決策樹2、決策樹3……決策樹Mn(這里我們將用4個模型來解釋)。在隨機森林中,我們使用決策樹來設計這些模型。我們從給定的數據集中采樣一些行和列。我們使用帶替換的行采樣,這意味著我們從數據集中取出一些行(?m )并選擇一些列(?d)作為特征樣本。這就是我們如何使用 bagging 為決策樹選擇行子集。決策樹中的記錄數始終小于數據集中的記錄數。
Number of Records : m*d
Number of Rows : d
Number of features(columns) : m
Number of rows selected for row sampling : d'
Number of features for feature sampling : nd' < d
n < m
????????這里我們有少量記錄,因此我們指定其中一些用于訓練。然后,我們對這些記錄進行采樣,并將它們提供給第一個決策樹。對第二個決策樹重復相同的過程,但使用替換采樣。當我們進行替換采樣時,并非所有記錄都會重復 - 相反,會獲取一個新樣本并將其提供給第二個決策樹。在此過程中,某些記錄和特征可能會重復,但許多記錄會發生變化。對于每個決策樹重復此行和特征采樣過程,每次使用不同的特征集。

????????行采樣(RS)+特征采樣(FS)
????????在給定數據上訓練決策樹后,它可以準確預測新測試數據的結果。在二元分類問題中,如果決策樹給出正(1)輸出,我們可以假設它是正(1)。為了做出最終預測,我們使用模型中的多數票。例如,如果模型 1、模型 2 和模型 4 假設輸出為 1,則我們假設它為正。
當我們使用多個決策樹時,我們需要考慮兩個屬性。
- 低偏差
- 高方差
????????如果我們創建一個完整深度的決策樹,它將具有低偏差和高方差,并且它將根據我們的訓練數據集進行適當的訓練。所以訓練誤差會非常低。
????????當決策樹由于新的測試數據而產生大量錯誤時,就會出現高方差。當決策樹創建到其完整深度時,就會發生這種情況,稱為過度擬合。在隨機森林中,使用多個決策樹,每個決策樹都具有高方差。然而,當使用多數投票組合這些決策樹時,高方差將轉換為低方差。這是通過在數據集中使用行和特征采樣來實現的。通過組合多個決策樹的輸出,可以降低高方差。
????????如果我們有 1000 條記錄并更改 200 條記錄,這將如何影響輸出?
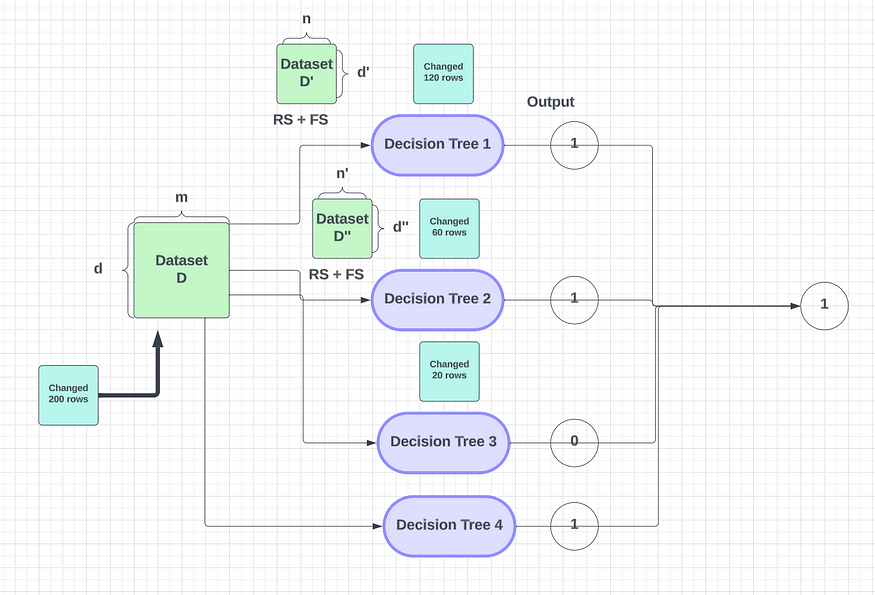
????????對輸出的影響
????????我們目前正在對 200 條記錄的每次決策樹更改進行行和特征采樣。這可確保 200 條記錄在決策樹之間正確劃分。一些記錄將進入決策樹 2 或 1,但此更改不會顯著影響決策樹的準確性或輸出。這是由于隨機森林的高方差特性,它適用于大多數機器學習用例。如果這是一個回歸問題,決策樹將給出一個連續值,我們可以取所有輸出的平均值或特定輸出的中位數。
????????在隨機森林中,特定輸出的中值取決于輸出的分布和決策樹的結構。通常,隨機森林的工作原理是查找所有決策樹的輸出平均值。然而,為了減少方差,我們使用多個決策樹、行采樣和特征采樣。
????????隨機森林既有分類器又有回歸。它們之間的唯一區別是分類器使用多數投票,而回歸器找到所有決策樹輸出的平均值或中值。通過調整超參數(例如決策樹的數量),您可以優化隨機森林的性能。
????????隨機森林或決策樹是否需要標準化(縮放)?
沒有!
- RF 的本質是收斂和數值精度問題(這些問題有時會影響邏輯回歸和線性回歸以及神經網絡中使用的算法)并不那么重要。因此,您不需要像使用神經網絡那樣將變量轉換為通用尺度。
- 您不會得到任何回歸系數的類似物,回歸系數測量每個預測變量與響應之間的關系。因此,您也不需要考慮如何解釋這些受可變測量尺度影響的系數。
這就是套袋技術中的隨機森林分類器和隨機森林回歸。在下一篇文章中,我們將學習 Boosting 技術。



【第六屆傳智杯-新增場次-程序設計挑戰賽解題分析詳解復盤】)










)




