文章目錄
- 1. 理論介紹
- 2. 實例解析
- 2.1. 實例描述
- 2.2. 代碼實現
- 2.2.1. 主要代碼
- 2.2.2. 完整代碼
- 2.2.3. 輸出結果
1. 理論介紹
- 線性模型泛化的可靠性是有代價的,因為線性模型沒有考慮到特征之間的交互作用,由此模型靈活性受限。
- 泛化性和靈活性之間的基本權衡被描述為偏差-方差權衡。
- 線性模型有很高的偏差,因此它們只能表示一小類函數,但其方差很低,因此它們在不同的隨機數據樣本上可以得出相似的結果。
- 神經網絡不局限于單獨查看每個特征,而是學習特征之間的交互,但即使我們有比特征多得多的樣本,深度神經網絡也有可能過擬合。
- 經典泛化理論認為,為了縮小訓練和測試性能之間的差距,應該以簡單的模型為目標。 簡單性以較小維度的形式展現,簡單性的另一個角度是平滑性,即函數不應該對其輸入的微小變化敏感。
- 暫退法在前向傳播過程中,計算每一內部層的同時注入噪聲。 因為當訓練一個有多層的深層網絡時,注入噪聲只會在輸入-輸出映射上增強平滑性。從表面上看是在訓練過程中丟棄(drop out)一些神經元。 在整個訓練過程的每一次迭代中,標準暫退法包括在計算下一層之前將當前層中的一些節點置零。
- 神經網絡過擬合與每一層都依賴于前一層激活值相關,這種情況稱為共適應性,而暫退法會破壞共適應性。
- 可以以一種無偏向的方式注入噪聲,在固定住其他層時,每一層的期望值等于沒有噪音時的值。
- 標準暫退正則化通過按未丟棄的節點的分數進行規范化來消除每一層的偏差,換言之,每個中間活性值 h h h以暫退概率 p p p由隨機變量 h ′ h' h′替換,即:
h ′ = { 0 概率為? p h 1 ? p 其他情況 \begin{aligned} h' = \begin{cases} 0 & \text{ 概率為 } p \\ \frac{h}{1-p} & \text{ 其他情況} \end{cases} \end{aligned} h′={01?ph???概率為?p?其他情況?? - 通常,我們在測試時不用暫退法。 給定一個訓練好的模型和一個新的樣本,我們不會丟棄任何節點,因此不需要標準化。 然而也有一些例外:一些研究人員在測試時使用暫退法, 用于估計神經網絡預測的不確定性: 如果通過許多不同的暫退法遮蓋后得到的預測結果都是一致的,那么我們可以說網絡發揮更穩定。
- 我們可以將暫退法應用于每個隱藏層的輸出(在激活函數之后), 并且可以為每一層分別設置暫退概率,常見的技巧是在靠近輸入層的地方設置較低的暫退概率。
2. 實例解析
2.1. 實例描述
使用具有兩個隱藏層的多層感知機和暫退法,擬合Fashion-MNIST數據集。
2.2. 代碼實現
2.2.1. 主要代碼
net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),nn.Dropout(0.2), # 暫退概率為0.2nn.Linear(256, 256),nn.ReLU(),nn.Dropout(0.5), # 暫退概率為0.5nn.Linear(256, 10)
).to(device)
2.2.2. 完整代碼
import os
from tensorboardX import SummaryWriter
from rich.progress import track
from torchvision.transforms import Compose, ToTensor
from torchvision.datasets import FashionMNIST
import torch
from torch.utils.data import DataLoader
from torch import nn, optimdef load_dataset():"""加載數據集"""root = "./dataset"transform = Compose([ToTensor()])mnist_train = FashionMNIST(root, True, transform, download=True)mnist_test = FashionMNIST(root, False, transform, download=True)dataloader_train = DataLoader(mnist_train, batch_size, shuffle=True, num_workers=num_workers,)dataloader_test = DataLoader(mnist_test, batch_size, shuffle=False,num_workers=num_workers,)return dataloader_train, dataloader_testif __name__ == '__main__':# 全局參數設置num_epochs = 10batch_size = 256num_workers = 3device = torch.device('cuda:0')lr = 0.5# 創建記錄器def log_dir():root = "runs"if not os.path.exists(root):os.mkdir(root)order = len(os.listdir(root)) + 1return f'{root}/exp{order}'writer = SummaryWriter(log_dir=log_dir())# 數據集配置dataloader_train, dataloader_test = load_dataset()# 定義模型net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),nn.Dropout(0.2),nn.Linear(256, 256),nn.ReLU(),nn.Dropout(0.5),nn.Linear(256, 10)).to(device)def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights)criterion = nn.CrossEntropyLoss(reduction='none')optimizer = optim.SGD(net.parameters(), lr=lr)# 訓練循環for epoch in track(range(num_epochs), description='dropout'):for X, y in dataloader_train:X, y = X.to(device), y.to(device)loss = criterion(net(X), y)optimizer.zero_grad()loss.mean().backward()optimizer.step()with torch.no_grad():train_loss, train_acc, num_samples = 0.0, 0.0, 0for X, y in dataloader_train:X, y = X.to(device), y.to(device)y_hat = net(X)loss = criterion(y_hat, y)train_loss += loss.sum()train_acc += (y_hat.argmax(dim=1) == y).sum()num_samples += y.numel()train_loss /= num_samplestrain_acc /= num_samplestest_acc, num_samples = 0.0, 0for X, y in dataloader_test:X, y = X.to(device), y.to(device)y_hat = net(X)test_acc += (y_hat.argmax(dim=1) == y).sum()num_samples += y.numel()test_acc /= num_sampleswriter.add_scalars('metrics', {'train_loss': train_loss,'train_acc': train_acc,'test_acc': test_acc}, epoch)writer.close()
2.2.3. 輸出結果
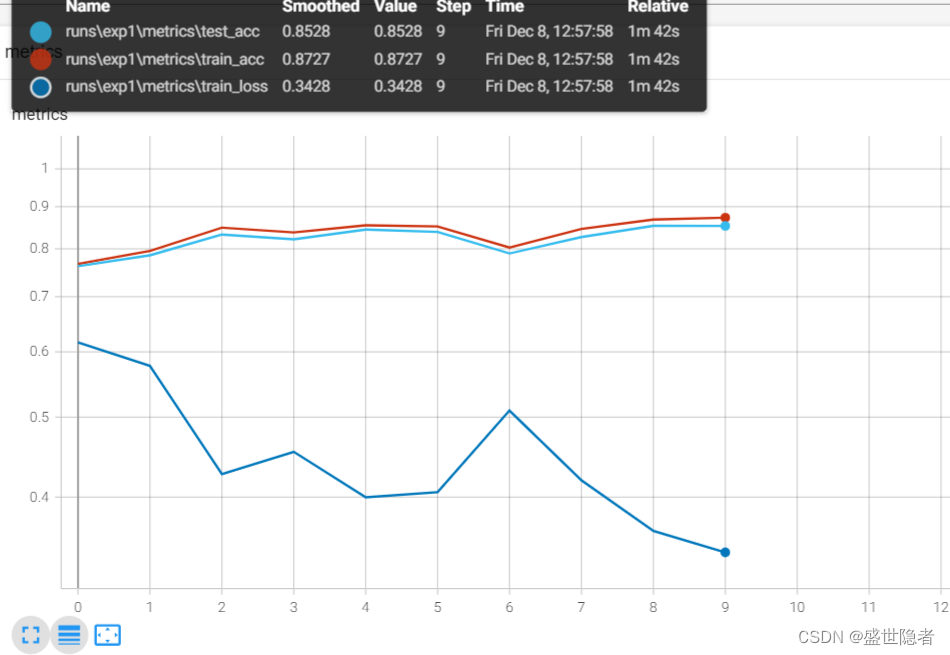





)

 高階函數詳解)

![[wp]“古劍山”第一屆全國大學生網絡攻防大賽 Web部分wp](http://pic.xiahunao.cn/[wp]“古劍山”第一屆全國大學生網絡攻防大賽 Web部分wp)





)

)
)
)