在計算機視覺中，相機標定是非常重要的一步，主要目的是從圖像中恢復出物體的三維信息。為了做到這一點，我們需要了解和使用一系列的數學工具，這些工具描述了相機的成像過程，包括相機的內參、外參、畸變系數、投影矩陣和矯正矩陣。
本文主要講解相機參數的格式與作用，相機標定可參考這篇博文相機標定

---

一、相機內參（Camera Intrinsics）

1.1 內參的定義

相機內參指的是描述相機光學成像系統內部幾何關系的參數。它主要涉及如何將三維空間中的點投影到二維圖像平面。具體來說，相機內參矩陣包含了相機的焦距、主點以及畸變系數等信息。

1.2 內參矩陣的固定格式

在進行開發時相機內參一般用如下格式表示cameraMatrix
cv::Mat_<double>(3, 3)
內參矩陣通常采用3x3的矩陣表示，格式如下：

$$K=\left[\begin{array}{ccc}{f}_x& s& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

其中：

• $f_x$ 和 $f_y$ 分別是相機在x和y方向的焦距，單位為像素，這兩個參數反映了圖像傳感器上每毫米對應的像素數量。通常情況下，焦距在水平方向和垂直方向可能不相等。
• $c_x$ 和 $c_y$ 是圖像的主點坐標，通常是圖像的中心點。如果圖像的分辨率為 $W\times H$，那么 $c_x=W/2$，$c_y=H/2$。
• $s$ 是切向畸變系數，通常在大部分相機中是零，除非相機鏡頭存在較嚴重的切向畸變。

該矩陣通過將三維世界坐標系中的點轉換為圖像坐標系中的點。

1.3 內參矩陣的作用

1. 將三維坐標轉化為二維坐標：內參矩陣的作用就是將世界坐標系中的三維點 $X,Y,Z$ 投影到相機的二維圖像坐標系中。

2. 校正畸變：內參矩陣中的一些參數，如焦距和主點，可以用來去畸變或者校正圖像中的幾何誤差。

3. 計算圖像尺寸和焦距：內參矩陣的 $f_x$ 和 $f_y$ 值可用于計算圖像中物體的實際物理尺寸或距離。

---

二、相機畸變系數（Distortion Coefficients）

2.1 畸變的定義

相機的畸變主要由光學鏡頭的特性引起。最常見的畸變有兩種：

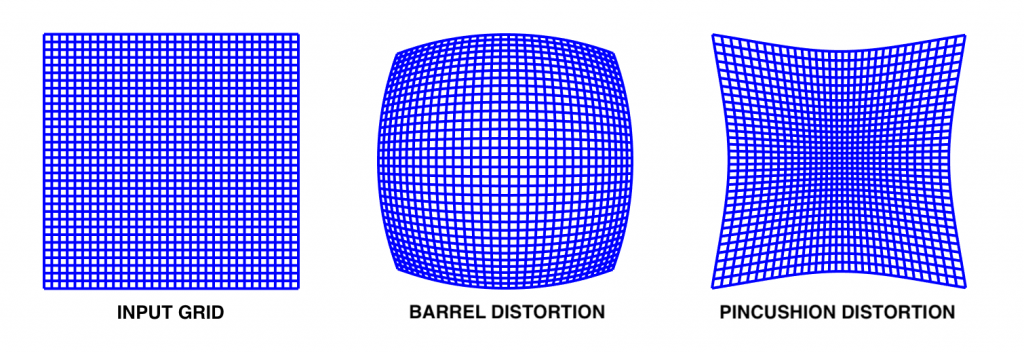
1. 徑向畸變：主要發生在圖像的四周，造成圖像的拉伸或壓縮，通常表現為桶形畸變或枕形畸變。
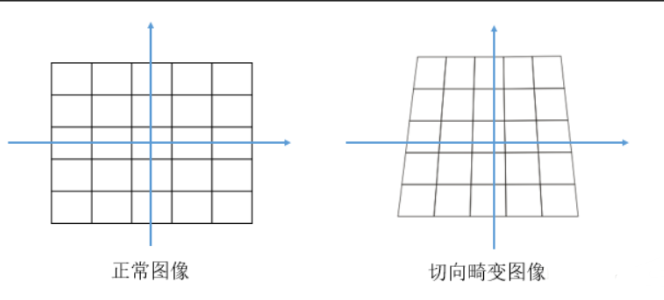
2. 切向畸變：通常是由相機鏡頭和圖像平面之間的非理想對準引起的，表現為圖像的傾斜或彎曲。
   
   

2.2 畸變系數的固定格式

開發中一般用如下代碼表示distCoeffs
cv::Mat_<double>(1, 5)
在標準的針孔相機模型中，畸變系數由以下五個參數表示：

$$D=[k_1,k_2,p_1,p_2,k_3]$$

• $k_1,k_2,k_3$ 是徑向畸變系數，描述圖像的徑向畸變。
• $p_1,p_2$ 是切向畸變系數，描述圖像的切向畸變。

2.3 畸變系數的作用

1. 去畸變：畸變系數用于矯正圖像中的畸變，特別是在使用廣角鏡頭時，畸變非常明顯。
2. 提高計算機視覺算法的精度：去除畸變后，圖像會更加接近真實的物理結構，進而提高目標識別、三維重建等算法的精度。

---

三、相機外參（Camera Extrinsics）

3.1 外參的定義

相機外參是描述相機與世界坐標系之間關系的參數。它通過旋轉矩陣（$R$)和位移向量（$T$）來表示。旋轉矩陣描述了相機坐標系與世界坐標系之間的旋轉關系，而位移向量描述了兩者之間的平移關系。

3.2 外參矩陣的格式

相機外參矩陣通常由一個 $3\times 3$ 的旋轉矩陣 $R$ 和一個 $3\times 1$ 的平移向量 $T$ 組成。外參矩陣通常是一個 $3\times 4$ 的矩陣：

$$[R|T]=\left[\begin{array}{cccc}{R}_{11}& R_{12}& R_{13}& T_x\\ R_{21}& R_{22}& R_{23}& T_y\\ R_{31}& R_{32}& R_{33}& T_z\end{array}\right]$$

其中：

• $R$ 是一個 $3\times 3$ 的旋轉矩陣，表示相機坐標系相對于世界坐標系的旋轉。
• $T$ 是一個 $3\times 1$ 的平移向量，表示相機坐標系原點相對于世界坐標系原點的平移。

3.3 外參矩陣的作用

1. 將世界坐標系的三維點轉化為相機坐標系的三維點：外參矩陣用于表示相機的位置和姿態，幫助我們將三維物體的坐標從世界坐標系轉換到相機坐標系。

2. 多視角對齊：在多視角計算中，相機的外參矩陣非常重要，尤其是在立體視覺和三維重建中，外參矩陣幫助我們理解相機之間的相對位置和角度。

---

四、投影矩陣（Projection Matrix）

4.1 投影矩陣的定義

投影矩陣是將三維世界坐標系中的點轉換為二維圖像坐標系中的點的矩陣。它綜合了相機的內參和外參信息，通過對三維點進行線性變換，將其投影到圖像平面。

4.2 投影矩陣的格式

投影矩陣通常由內參矩陣 $K$ 和外參矩陣 $[R|T]$ 組成，形式如下：

$$P=K[R|T]$$

其中：

• $K$ 是內參矩陣，描述了相機的內部幾何參數。
• $[R|T]$ 是外參矩陣，描述了相機在世界坐標系中的旋轉和平移。

通過這個矩陣，我們可以將三維世界坐標系中的點 $X,Y,Z$ 投影到二維圖像坐標系 $x,y$。

4.3 投影矩陣的作用

1. 三維點到二維圖像點的映射：投影矩陣能夠將相機坐標系下的三維點 $X,Y,Z$ 映射為圖像平面上的二維點 $x,y$，并將這些點用于后續的圖像處理、目標檢測等任務。

2. 計算視差和三維重建：在立體視覺和三維重建中，投影矩陣幫助我們從不同視角的圖像中恢復物體的三維結構。

---

五、矯正矩陣（Rectification Matrix）

5.1 矯正矩陣的定義

矯正矩陣用于去除立體視覺系統中由于相機不同視角引起的幾何誤差。通常在立體匹配和深度估計中，矯正矩陣將左右圖像對齊到相同的圖像平面，消除由視角差異造成的幾何失真。

5.2 矯正矩陣的格式

在立體相機系統中，左右相機的矯正矩陣由旋轉矩陣 $R_1,R_2$ 和投影矩陣 $P_1,P_2$ 組成，用來調整圖像，使得圖像上的同名點在同一掃描線中。矯正矩陣的格式通常為：

$$[R_1|T_1]=\text{Rectification?Matrix?for?the?left?camera}$$

$$[R_2|T_2]=\text{Rectification?Matrix?for?the?right?camera}$$

5.3 矯正矩陣的作用

1. 去除視差誤差：矯正矩陣消除了由于相機視角差異引起的幾何畸變，使得圖像對齊，從而進行精確的視差計算。

2. 提高深度估計精度：在深度估計過程中，矯正矩陣使得左右圖像的對應點對齊，有助于提高深度圖的精度。

---