在用cox回歸做分析時，我們一般會得出各種變量在結局的風險影響（HR大于1，就代表變量值增大，對應結局影響的風險就隨之增大），但是這里有個壞處是，cox回歸得到的是瞬時風險值，我們最多得到一段時間，這個變量的影響。

而PH檢驗，就是為了驗證變量對結局的風險影響是否會隨時間變化，如果不會，那么求得的p值就會大于0.05，也就說明回歸里的HR值的可解釋性高。

以下是一個例子：

# 加載生存分析包
library(survival)
library(survminer) # 用于PH檢驗和繪圖# 生成數據（100個樣本）
set.seed(123)
n <- 100
group <- sample(c("Treatment", "Placebo"), n, replace = TRUE)
time <- ifelse(group == "Treatment", rexp(n, rate = 0.1),  # 治療組風險更低rexp(n, rate = 0.2))   # 安慰劑組風險更高
status <- rbinom(n, 1, 0.8)  # 80%的事件觀察到（1=事件發生，0=刪失）# 創建數據框
df <- data.frame(time, status, group)
head(df)# 擬合Cox模型
cox_model <- coxph(Surv(time, status) ~ group, data = df, ties = "breslow")
summary(cox_model)# PH檢驗（全局檢驗）
ph_test <- cox.zph(cox_model)
print(ph_test)# 可視化檢驗結果（ Schoenfeld殘差 vs 時間）
ggcoxzph(ph_test)

輸出：

Call:
coxph(formula = Surv(time, status) ~ group, data = df, ties = "breslow")n= 100, number of events= 77 coef exp(coef) se(coef)      z Pr(>|z|)
groupTreatment -0.2469    0.7813   0.2440 -1.012    0.312exp(coef) exp(-coef) lower .95 upper .95
groupTreatment    0.7813       1.28    0.4843      1.26Concordance= 0.52  (se = 0.032 )
Likelihood ratio test= 1  on 1 df,   p=0.3
Wald test            = 1.02  on 1 df,   p=0.3
Score (logrank) test = 1.03  on 1 df,   p=0.3chisq df    p
group   0.34  1 0.56
GLOBAL  0.34  1 0.56

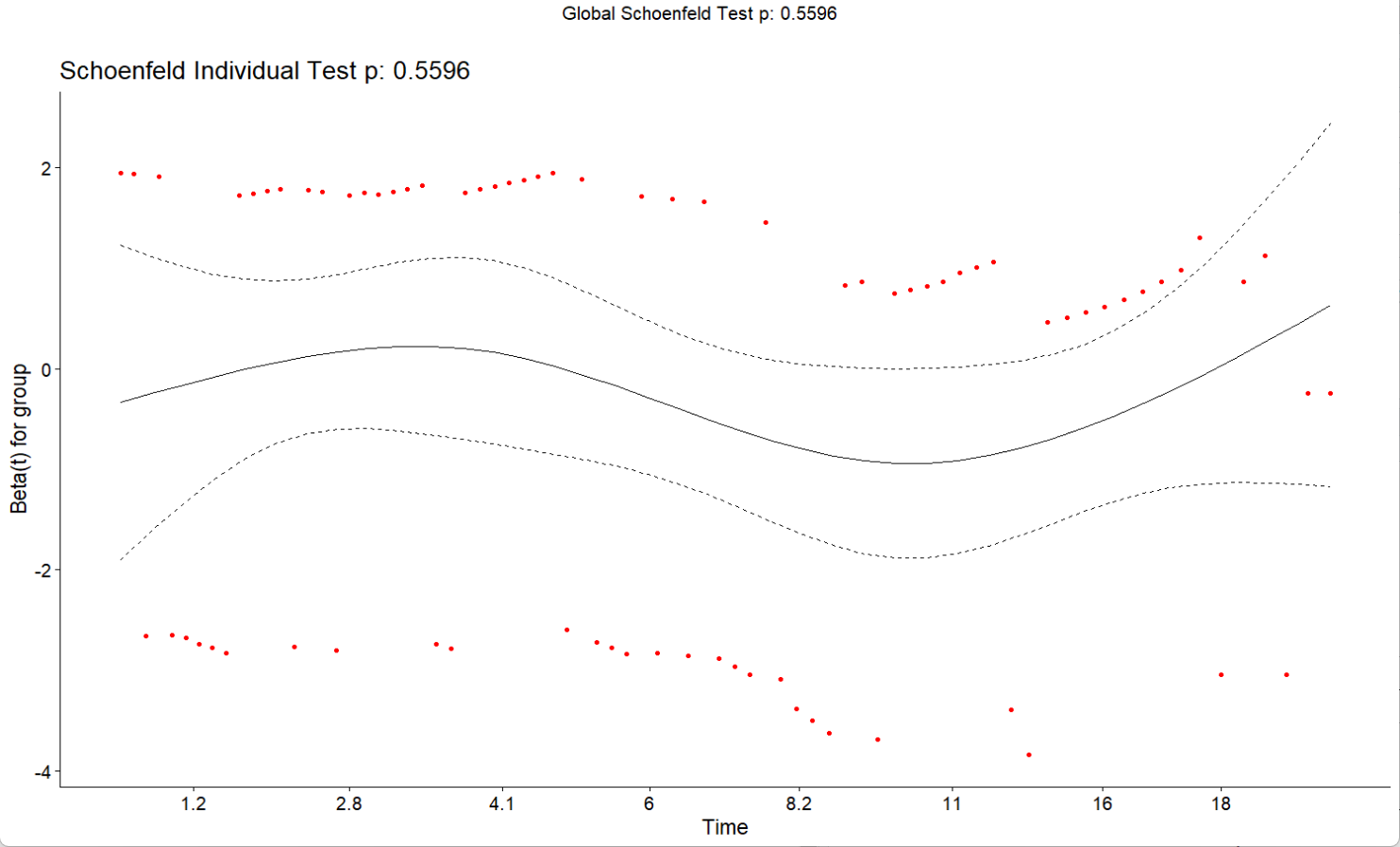
結果表明，雖然group在cox回歸的p值較低，HR也小于1，但是group和global的PH是大于0.05的，這可能意味著方向是對的，只是特征要處理一下，或者是要剖析一下結果。