目錄

一、快速走進和理解Mamba建模架構

（一）從Transformer的統治地位談起

（二）另一條道路：結構化狀態空間模型（SSM）

（三）Mamba 的核心創新：Selective SSM + 簡潔架構

1. 引入選擇性機制（Selectivity）

2. 設計硬件友好的并行遞歸算法

3. 極簡神經網絡架構

二、State Space Models：結構化狀態空間模型的前世今生

（一）從連續系統到離散建模：S4 的核心結構

（二）離散化（Discretization）：從連續動態到可微計算圖

（三）高維狀態空間與 GPU 親和性

（四）SSM 家族譜：S4 是誰的“兒子”？誰又是它的“繼承人”？

三、選擇性狀態空間模型（Selective State Space Models）

（一）動機：選擇性是一種壓縮機制

（二）引入選擇機制到 SSM 中

（三）高效實現選擇性 SSM

（四）一個極簡的 SSM 架構

1. 與門控機制的關系：RNN 門控機制其實是一種選擇機制的特例

2. 對選擇機制的三種直覺解釋

2.1?可變時間間隔（Variable Spacing）

2.2?上下文過濾（Filtering Context）

2.3?邊界重置（Boundary Resetting）

3. 選擇機制中各參數的解釋與擴展

Δ（Delta）控制輸入選擇程度

A 控制動力系統的衰減/更新速率

B 和 C 提供更精細的狀態輸入輸出控制

四、實證評估（Empirical Evaluation）

（一）合成任務驗證選擇能力（Synthetic Tasks）

1. 選擇性拷貝任務（Selective Copying）

2. 歸納頭任務（Induction Heads）

（二）語言建模（Language Modeling）

1. Scaling Law 實驗

2. Zero-shot 下游評估

（三） DNA Sequence Modeling

（四）Audio Waveform Generation

（五） 計算效率評估

（六）架構與機制消融實驗

（七）? 總結：Mamba 的實證貢獻

五、總結與展望：Mamba 的意義與未來方向

---

干貨分享，感謝您的閱讀！

基礎模型現在推動著深度學習中大部分令人興奮的應用，幾乎普遍基于Transformer架構及其核心注意力模塊。為了應對Transformer在長序列上的計算低效，已經提出了許多子平方時間架構，如線性注意力、門控卷積和遞歸模型，以及結構化狀態空間模型（SSM）。然而，這些模型在語言等重要模態上，表現往往不如注意力機制。我們發現，諸如上述模型的一個關鍵弱點是它們無法進行基于內容的推理，并提出了若干改進。首先，簡單地讓SSM參數成為輸入的函數，解決了其在離散模態中的弱點，允許模型根據當前token有選擇性地在序列長度維度上傳播或遺忘信息。其次，盡管這一改變阻止了高效卷積的使用，但我們設計了一個硬件感知的并行算法，支持遞歸模式。我們將這些選擇性SSM集成到一個簡化的端到端神經網絡架構中，該架構無需注意力或甚至MLP模塊（Mamba）。Mamba在推理速度上具有顯著優勢（比Transformer高出5倍吞吐量），且在序列長度上呈線性擴展，其在實際數據上的表現對于百萬長度的序列有所提升。作為一種通用的序列模型骨架，Mamba在語言、音頻和基因組學等多個模態上都達到了最先進的性能。在語言建模任務上，我們的Mamba-3B模型超越了相同規模的Transformer，并且在預訓練和下游評估中與規模為其兩倍的Transformer相當。

1 引言

基礎模型（FMs），即在大量數據上預訓練然后調整用于下游任務的大型模型，已經成為現代機器學習中的一種有效范式。這些基礎模型的骨干通常是序列模型，能夠處理來自各種領域的任意輸入序列，如語言、圖像、語音、音頻、時間序列和基因組學（Brown et al. 2020; Dosovitskiy et al. 2020; Ismail Fawaz et al. 2019; Oord et al. 2016; Poli et al. 2023; Sutskever, Vinyals, 和 Quoc V Le 2014）。盡管這一概念對模型架構的選擇沒有特定要求，但現代基礎模型主要基于單一類型的序列模型：Transformer（Vaswani et al. 2017）及其核心注意力層（Bahdanau, Cho, 和 Bengio 2015）。自注意力機制的有效性歸功于其能夠在上下文窗口內密集地路由信息，從而使其能夠建模復雜的數據。然而，這一特性帶來了根本性的缺陷：無法建模窗口外的信息，并且在窗口長度上具有平方級的計算復雜度。大量的研究已經提出了更高效的注意力變體來克服這些缺點（Tay, Dehghani, Bahri, 等，2022），但往往以犧牲其有效性的某些特性為代價。到目前為止，尚未有這些變體在各個領域的規模上被證明具有實證效果。

最近，結構化狀態空間序列模型（SSMs）（Gu, Goel, 和 Ré 2022; Gu, Johnson, Goel, 等，2021）作為一種有前景的序列建模架構出現。這些模型可以被解釋為遞歸神經網絡（RNNs）和卷積神經網絡（CNNs）的結合，受到經典狀態空間模型（Kalman 1960）的啟發。這類模型能夠非常高效地進行計算，無論是以遞歸方式還是卷積方式，都在序列長度上實現線性或接近線性的擴展。此外，它們具有建模長程依賴的原則性機制（Gu, Dao, 等，2020），并且在長程領域基準如長程競技場（Long Range Arena）中占據主導地位（Tay, Dehghani, Abnar, 等，2021）。許多種類的SSM（Gu, Goel, 和 Ré 2022; Gu, Gupta, 等，2022; Gupta, Gu, 和 Berant 2022; Y. Li 等，2023; Ma 等，2023; Orvieto 等，2023; Smith, Warrington, 和 Linderman 2023）在處理連續信號數據如音頻和視覺等領域取得了成功（Goel et al. 2022; Nguyen, Goel, 等，2022; Saon, Gupta, 和 Cui 2023）。然而，在處理離散和信息密集型數據如文本時，它們的效果較差。

我們提出了一類新的選擇性狀態空間模型，通過在多個方面改進，實現在序列長度上線性擴展的同時，具備Transformer的建模能力。

選擇機制

首先，我們識別了先前模型的一個關鍵限制：能夠根據輸入有效地選擇數據（即關注或忽略特定的輸入）。基于在一些重要的合成任務（如選擇性復制和歸納頭）中的直覺，我們通過基于輸入對SSM參數進行參數化來設計一個簡單的選擇機制。這使得模型能夠過濾掉無關的信息，并永遠記住相關信息。

硬件感知算法

這一簡單的改變為模型的計算帶來了技術挑戰；事實上，所有先前的SSM模型必須是時間和輸入不變的，以保持計算的高效性。我們通過一個硬件感知的算法來克服這一挑戰，該算法通過掃描而非卷積遞歸計算模型，但不會實現擴展狀態，以避免在GPU內存層次結構之間進行I/O訪問。結果，新的實現比以前的方法更快，理論上（在序列長度上線性擴展，相較于所有基于卷積的SSM的偽線性擴展）和在現代硬件上（在A100 GPU上速度提高最多3倍）。

架構

我們通過將先前SSM架構的設計（Dao, Fu, Saab, 等，2023）與Transformer的MLP模塊結合，簡化了先前的深度序列模型架構，從而得到了一個簡單且同質的架構設計（Mamba），并融入了選擇性狀態空間。

選擇性SSM，以及由此擴展的Mamba架構，是完全遞歸的模型，具有一些使其適合作為操作序列的通用基礎模型骨干的關鍵屬性。
(i) 高質量：選擇性使得其在像語言和基因組學等密集模態上表現出色。
(ii) 快速訓練和推理：在訓練過程中，計算和內存在序列長度上線性擴展，且在推理時每一步僅需常數時間，因為它不需要緩存之前的元素。
(iii) 長上下文：質量和效率的結合帶來了在實際數據上的性能提升，序列長度可擴展到1M。

我們通過實驗證明了Mamba作為通用序列基礎模型骨干的潛力，展示了其在預訓練質量和領域特定任務表現方面，在多個模態和設置下的優勢：

? 合成任務。 在一些重要的合成任務，如復制和歸納頭（這些任務被認為是大型語言模型的關鍵任務）上，Mamba不僅能夠輕松解決它們，而且能夠無限地推斷解決方案（>1M tokens）。
? 音頻和基因組學。 Mamba在音頻波形和DNA序列建模任務上超越了先前的最先進模型，如SaShiMi、Hyena和Transformers，在預訓練質量和下游評估指標（例如，在一個具有挑戰性的語音生成數據集上，FID降低了一半以上）上均表現優異。在這兩種設置中，其性能隨著上下文長度的增加，能夠處理百萬長度的序列。
? 語言建模。 Mamba是首個真正實現Transformer級別性能的線性時間序列模型，無論是在預訓練困惑度還是下游評估中。通過擴展到1B參數的規模，我們展示了Mamba超越了大量基準，包括基于LLaMa（Touvron et al. 2023）的現代Transformer訓練方法。我們的Mamba語言模型相比相同規模的Transformer具有5倍的生成吞吐量，且Mamba-3B的質量與其兩倍規模的Transformer相當（例如，在常識推理上比Pythia-3B高出4個點，甚至超越了Pythia-7B）。

模型代碼和預訓練檢查點已開源，地址為：https://github.com/state-spaces/mamba。

2 狀態空間模型

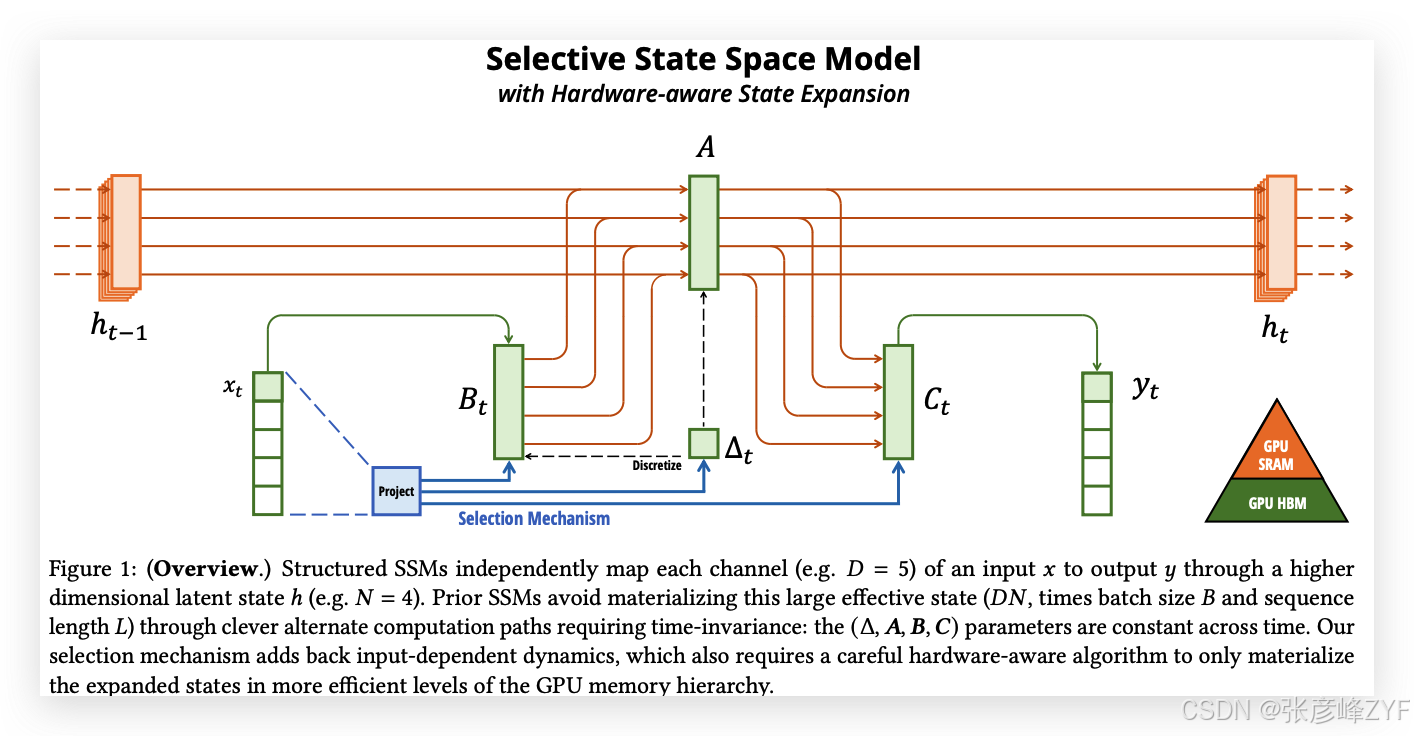
結構化狀態空間序列模型（S4）是近年來為深度學習提出的一類序列模型，廣泛與遞歸神經網絡（RNNs）、卷積神經網絡（CNNs）和經典的狀態空間模型相關。它們的靈感來自于特定的連續系統（1），該系統通過一個隱式的潛在狀態 ?(𝑡) ∈ ?^𝑁，將一維函數或序列 𝑥(𝑡) ∈ ? 映射到 𝑦(𝑡) ∈ ?。

具體而言，S4 模型通過四個參數（Δ, 𝑨, 𝑩, 𝑪）定義，這些參數在兩個階段中定義了一個序列到序列的轉換：

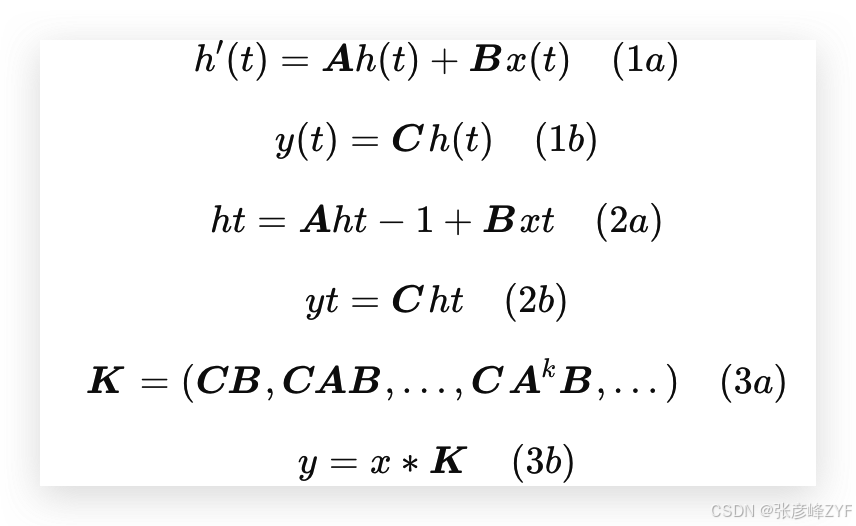
離散化

第一階段將“連續參數”（Δ, 𝑨, 𝑩）轉化為“離散參數”（𝑨, 𝑩），通過固定的公式 𝑨 = 𝑓𝐴(Δ, 𝑨) 和 𝑩 = 𝑓𝐵(Δ, 𝑨, 𝑩)，其中對（𝑓𝐴, 𝑓𝐵）的組合稱為離散化規則。可以使用不同的規則，比如在方程（4）中定義的零階保持（ZOH）：

離散化與連續時間系統有深刻的聯系，這使它們具備額外的屬性，如分辨率不變性（Nguyen, Goel, 等，2022），并自動確保模型是適當歸一化的（Gu, Johnson, Timalsina, 等，2023；Orvieto 等，2023）。它還與RNN的門控機制相關（Gu, Gulcehre, 等，2020；Tallec 和 Ollivier，2018），我們將在第3.5節中回顧這一點。然而，從機械的角度來看，離散化可以簡單地視為在SSM的前向計算圖中的第一步。

SSM的其他變體可以跳過離散化步驟，直接對（𝑨, 𝑩）進行參數化（Zhang 等，2023），這可能更容易理解。

計算

在參數從（Δ, 𝑨, 𝑩, 𝑪）轉化為（𝑨, 𝑩, 𝑪）后，模型可以通過兩種方式計算：要么作為線性遞歸（2），要么作為全局卷積（3）。

通常，模型在訓練時使用卷積模式（3），以便高效并行訓練（在該模式下，整個輸入序列會一次性看到）；而在推理時則切換到遞歸模式（2），以便高效的自回歸推理（此時輸入一次看到一個時間步）。

線性時間不變性（LTI）

方程（1）到（3）的一個重要性質是，模型的動態是時間不變的。換句話說，（Δ, 𝑨, 𝑩, 𝑪），因此（𝑨, 𝑩）在所有時間步長中都是固定的。這個屬性稱為線性時間不變性（LTI），它與遞歸和卷積深刻相關。非正式地，我們認為LTI SSM相當于任何線性遞歸（2a）或卷積（3b），并將LTI作為這些模型類別的總稱。

到目前為止，所有結構化SSM都是LTI的（例如，作為卷積計算），因為基本的效率約束（在第3.3節中討論）。然而，這項工作的核心見解是，LTI模型在建模某些類型的數據時存在根本性的局限性，我們的技術貢獻在于移除LTI約束，同時克服效率瓶頸。

結構與維度

最后，我們注意到，結構化SSM被稱為“結構化”，是因為高效地計算它們還需要在𝑨矩陣上施加結構。最常見的結構形式是對角形式（Gu, Gupta, 等，2022；Gupta, Gu, 和 Berant，2022；Smith, Warrington, 和 Linderman，2023），我們也使用這種形式。

在這種情況下，𝑨 ∈ ?^(𝑁 × 𝑁)，𝑩 ∈ ?^(𝑁 × 1)，𝑪 ∈ ?^(1 × 𝑁)矩陣可以由𝑁個數字表示。為了對批量大小為𝐵、長度為𝐿、具有𝐷通道的輸入序列𝑥進行操作，SSM會獨立地應用于每個通道。請注意，在這種情況下，總的隱藏狀態的維度是每個輸入的𝐷𝑁，并且在序列長度上計算它需要𝑂(𝐵𝐿𝐷𝑁)的時間和內存；這是第3.3節中解決的基本效率瓶頸的根源。

一般狀態空間模型

我們注意到，狀態空間模型這一術語具有非常廣泛的意義，簡單地表示任何具有潛在狀態的遞歸過程。它已經被用來指代不同學科中的許多不同概念，包括馬爾科夫決策過程（MDP）（強化學習（Hafner et al. 2020））、動態因果建模（DCM）（計算神經科學（Friston, Harrison, 和 Penny 2003））、卡爾曼濾波器（控制（Kalman 1960））、隱馬爾可夫模型（HMM）和線性動力學系統（LDS）（機器學習），以及大型遞歸（有時也包括卷積）模型（深度學習）。

在本文中，我們將“SSM”這一術語專門用于指代結構化SSM類或S4模型（Gu, Goel, 和 Ré，2022；Gu, Gupta, 等，2022；Gupta, Gu, 和 Berant，2022；Hasani 等，2023；Ma 等，2023；Smith, Warrington, 和 Linderman，2023），并將這些術語互換使用。為了方便起見，我們還可能包括這類模型的衍生物，例如那些側重于線性遞歸或全局卷積視角的模型（Y. Li 等，2023；Orvieto 等，2023；Poli 等，2023），并在必要時澄清細微差別。

SSM架構

SSM是獨立的序列變換，可以被集成到端到端的神經網絡架構中（我們有時也稱SSM架構為SSNNs，它們與CNN層的關系類似，作為SSM層的實現）。我們討論一些最著名的SSM架構，其中許多也將作為我們的主要基準。

? 線性注意力（Katharopoulos 等，2020）是自注意力的近似，它涉及到一個遞歸過程，可以視為一種退化的線性SSM。
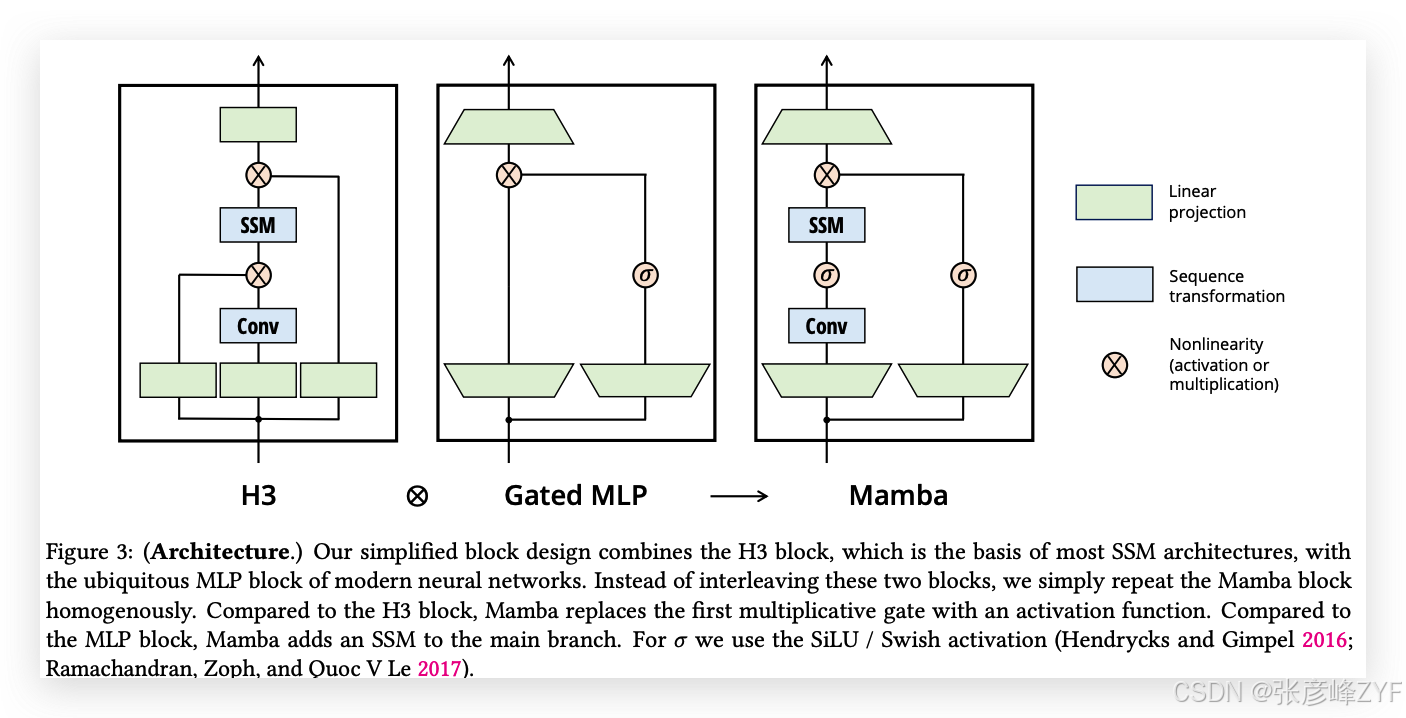
? H3（Dao, Fu, Saab, 等，2023）將這種遞歸推廣到使用S4；它可以被視為一種架構，其中一個SSM被兩個門控連接夾在中間（圖3）。H3還在主SSM層之前插入了一個標準的局部卷積，將其框定為一個移位SSM。
? Hyena（Poli 等，2023）使用與H3相同的架構，但將S4層替換為一個MLP參數化的全局卷積（Romero 等，2021）。
? RetNet（Y. Sun 等，2023）在架構中增加了一個附加門控，并使用了一個更簡單的SSM，允許一種替代的并行計算路徑，使用多頭注意力（MHA）的變體替代卷積。
? RWKV（B. Peng 等，2023）是最近為語言建模設計的RNN，基于另一種線性注意力近似——無注意力Transformer（S. Zhai 等，2021）。它的主要“WKV”機制涉及LTI遞歸，并且可以視為兩個SSM的比值。

其他與SSM及其架構密切相關的內容將在擴展的相關工作部分（附錄B）中進一步討論。我們特別突出S5（Smith, Warrington, 和 Linderman，2023）、QRNN（Bradbury 等，2016）和SRU（Lei 等，2017），它們是與我們的核心選擇性SSM最為相關的方法。

3 選擇性狀態空間模型

我們通過合成任務的直覺來激發選擇機制（第3.1節），然后解釋如何將該機制融入狀態空間模型（第3.2節）。由此產生的時變SSM無法使用卷積，這提出了如何高效計算它們的技術挑戰。我們通過利用現代硬件上的內存層次結構來克服這一挑戰（第3.3節）。接著，我們描述了一種簡單的SSM架構，不需要注意力機制或MLP模塊（第3.4節）。最后，我們討論了選擇機制的其他一些特性（第3.5節）。

3.1 動機：選擇作為壓縮的一種方式

我們認為序列建模的一個根本問題是將上下文壓縮到一個更小的狀態中。事實上，我們可以從這個角度來看待流行序列模型的權衡。例如，注意力機制既有效又低效，因為它明確地不壓縮上下文。這可以從自回歸推理需要顯式地存儲整個上下文（即KV緩存）這一事實中看出，這直接導致了Transformer的線性時間推理和二次時間訓練的慢速性。另一方面，遞歸模型之所以高效，是因為它們具有有限的狀態，這意味著常數時間推理和線性時間訓練。然而，它們的有效性受到該狀態壓縮上下文的能力的限制。

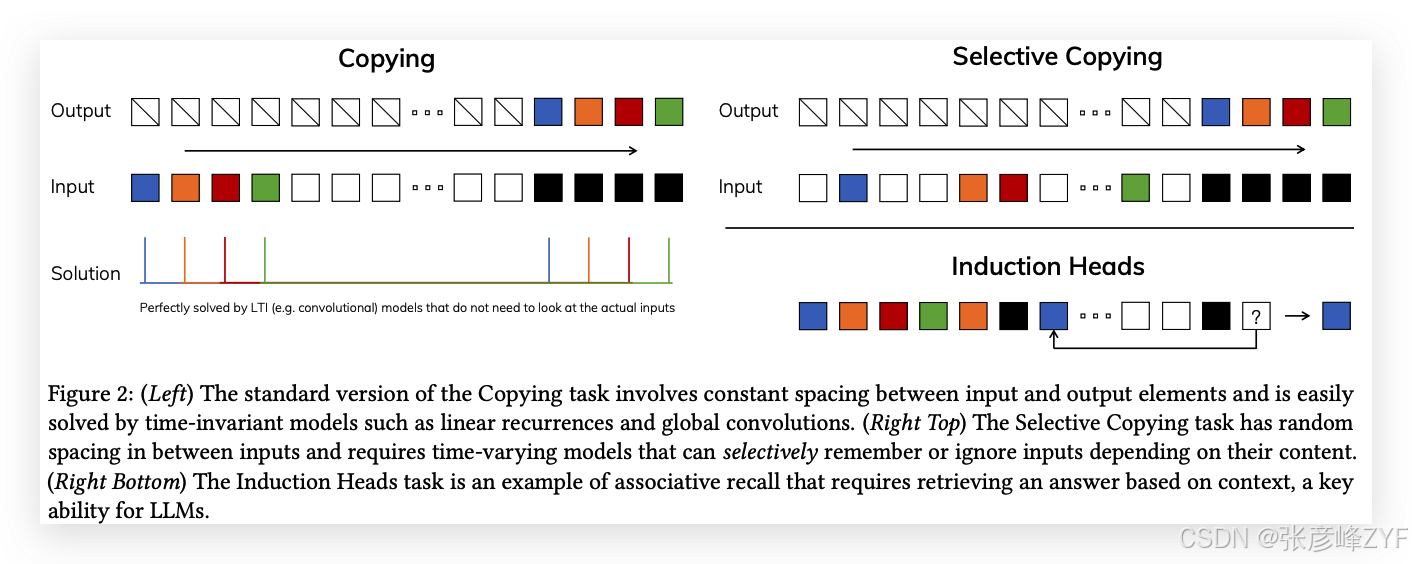
為了理解這個原理，我們集中討論兩個合成任務的例子（圖2）。

• 選擇性復制任務：通過改變要記住的標記位置，修改了流行的復制任務（Arjovsky, Shah, 和 Bengio 2016）。它需要內容感知推理，能夠記住相關標記（彩色的）并過濾掉不相關的標記（白色的）。

• 歸納頭任務：這是一個廣為人知的機制，假設能夠解釋大多數大語言模型（LLM）的上下文學習能力（Olsson 等，2022）。它需要上下文感知推理，以便在適當的上下文中知道何時生成正確的輸出（黑色的）。

這些任務揭示了LTI模型的失敗模式。從遞歸的角度來看，它們的常數動態（例如方程（2）中的（𝑨, 𝑩）轉移）無法讓它們從上下文中選擇正確的信息，或以輸入依賴的方式影響沿序列傳遞的隱藏狀態。從卷積的角度來看，已知全局卷積可以解決經典的復制任務（Romero 等，2021），因為它只需要時間感知，但它們在處理選擇性復制任務時遇到困難，因為缺乏內容感知（圖2）。更具體地說，輸入到輸出之間的間隔是變化的，而靜態卷積核無法建模這種變化。

總之，序列模型的效率與有效性權衡由它們壓縮狀態的能力來表征：高效模型必須有一個較小的狀態，而有效模型必須有一個包含上下文中所有必要信息的狀態。因此，我們提出構建序列模型的一個根本原則是選擇性：即有上下文感知的能力，能夠聚焦或過濾輸入到序列狀態中的信息。特別地，選擇機制控制信息沿序列維度的傳播或交互（有關更多討論，請參見第3.5節）。

3.2 通過選擇機制改進SSM

將選擇機制引入模型的一種方法是使其影響序列中交互的參數（例如RNN的遞歸動態或CNN的卷積核）依賴于輸入。

算法1和算法2展示了我們使用的主要選擇機制。其主要區別僅僅在于使幾個參數Δ、𝑩、𝑪成為輸入的函數，并且在整個過程中相應地改變了張量的形狀。特別地，我們強調這些參數現在具有一個長度維度𝐿，這意味著模型從時間不變變為時間變化。（請注意，形狀注解已在第2節中描述。）這使得其與卷積（3）之間的等價性喪失，從而對效率產生影響，接下來我們將討論這一點。

我們特別選擇𝑠𝐵(𝑥) = Linear𝑁(𝑥)，𝑠𝐶(𝑥) = Linear𝑁(𝑥)，𝑠Δ(𝑥) = Broadcast𝐷(Linear1(𝑥))，以及𝜏Δ = softplus，其中Linear𝑑表示參數化的投影到維度𝑑。選擇𝑠Δ和𝜏Δ的原因是它們與第3.5節中解釋的RNN門控機制的連接。

3.3 選擇性SSM的高效實現

硬件友好的原語，如卷積（Krizhevsky, Sutskever, 和 Hinton 2012）和注意力機制（Bahdanau, Cho, 和 Bengio 2015；Vaswani 等，2017），已廣泛應用。我們在此的目標是使選擇性SSM在現代硬件（如GPU）上同樣高效。選擇機制是相當自然的，早期的工作嘗試將選擇的特殊情況融入其中，例如讓Δ在遞歸SSM中隨時間變化（Gu, Dao 等，2020）。然而，正如之前所提到的，SSM使用中的一個核心限制是其計算效率，這也是為什么S4及其所有衍生物使用LTI（非選擇性）模型，通常以全局卷積的形式出現。

3.3.1 先前模型的動機

我們首先重新審視這一動機，并概述我們克服先前方法局限性的方式。

• 從高層次來看，遞歸模型如SSM始終在表現力和速度之間進行權衡：正如第3.1節所討論的，具有更大隱藏狀態維度的模型應當更有效，但更慢。因此，我們希望在不增加速度和內存成本的情況下，最大化隱藏狀態維度。

• 請注意，遞歸模式比卷積模式更靈活，因為后者（3）是通過擴展前者（2）得出的（Gu, Goel, 和 Ré 2022；Gu, Johnson, Goel 等，2021）。然而，這將要求計算并物化潛在狀態?，其形狀為（B, L, D, N），遠大于輸入𝑥和輸出𝑦的形狀（B, L, D），差距為𝑁（SSM狀態維度）倍。因此，引入了更高效的卷積模式，該模式可以繞過狀態計算并物化一個大小僅為（B, L, D）的卷積核（3a）。

• 先前的LTI狀態空間模型利用遞歸-卷積雙重形式，通過一個因子𝑁（≈ 10 ? 100）增加有效狀態維度，比傳統的RNN大得多，而不會產生效率損失。

3.3.2 選擇性掃描概述：硬件感知的狀態擴展

選擇機制的設計旨在克服LTI模型的局限性；與此同時，我們需要重新審視SSM的計算問題。我們通過三種經典技術來解決這個問題：核融合、并行掃描和重計算。我們做出了兩個主要觀察：

• 樸素的遞歸計算需要𝑂(𝐵𝐿𝐷𝑁) FLOP，而卷積計算需要𝑂(𝐵𝐿𝐷 log(𝐿)) FLOP，前者具有較低的常數因子。因此，對于長序列和不是特別大的狀態維度𝑁，遞歸模式實際上可以使用更少的FLOP。

• 兩個挑戰是遞歸的順序性質和大的內存使用。為了應對后者，就像卷積模式一樣，我們可以嘗試不實際物化完整的狀態?。

主要思想是利用現代加速器（GPU）的特性，僅在內存層次結構中更高效的級別中物化狀態?。特別地，大多數操作（除了矩陣乘法）都受內存帶寬的限制（Dao, Fu, Ermon 等，2022；Ivanov 等，2021；Williams, Waterman, 和 Patterson 2009）。這包括我們的掃描操作，我們使用核融合來減少內存I/O的數量，從而顯著加速相較于標準實現。

具體來說，我們不在GPU HBM（高帶寬內存）中準備掃描輸入（𝑨, 𝑩），而是將SSM參數（Δ, 𝑨, 𝑩, 𝑪）直接從較慢的HBM加載到快速SRAM，在SRAM中執行離散化和遞歸操作，然后將最終的輸出（大小為（B, L, D））寫回到HBM中。

為了避免順序遞歸，我們觀察到，盡管遞歸不是線性的，它仍然可以使用高效的并行掃描算法（Blelloch 1990；Martin 和 Cundy 2018；Smith, Warrington, 和 Linderman 2023）進行并行化。

最后，我們還必須避免保存反向傳播所需的中間狀態。我們巧妙地應用了經典的重計算技術，以減少內存需求：中間狀態不會被存儲，而是在反向傳播時，在將輸入從HBM加載到SRAM時重新計算。因此，融合的選擇性掃描層具有與優化后的Transformer實現（使用FlashAttention）相同的內存需求。

融合核和重計算的詳細信息見附錄D。完整的選擇性SSM層和算法如圖1所示。

3.4 簡化的SSM架構

與結構化SSM一樣，選擇性SSM是獨立的序列轉換，可以靈活地集成到神經網絡中。H3架構是最著名的SSM架構的基礎（第2節），這些架構通常由一個受到線性注意力啟發的模塊和一個MLP（多層感知機）模塊交替組成。我們通過將這兩個組件合并成一個，簡化了這一架構，并將其均勻地堆疊（圖3）。這一靈感來源于門控注意力單元（GAU）（Hua 等，2022），其為注意力機制做了類似的處理。

這一架構通過可控的擴展因子𝐸擴展模型維度𝐷。對于每個模塊，大多數參數（3𝐸𝐷2）位于線性投影中（輸入投影為2𝐸𝐷2，輸出投影為𝐸𝐷2），而內部SSM的貢獻較小。與此相比，SSM參數的數量（Δ、𝑩、𝑪的投影以及矩陣𝑨）要小得多。我們重復該模塊，并與標準的歸一化和殘差連接交替使用，形成Mamba架構。在實驗中，我們始終固定𝐸 = 2，并使用兩層該模塊來匹配Transformer的交錯MHA（多頭注意力）和MLP模塊的12𝐷2參數。我們使用SiLU / Swish激活函數（Hendrycks 和 Gimpel，2016；Ramachandran, Zoph 和 Quoc V Le，2017），這樣可以使得門控MLP變為流行的“SwiGLU”變體（Chowdhery 等，2023；Dauphin 等，2017；Shazeer，2020；Touvron 等，2023）。

最后，我們還使用了一個可選的歸一化層（我們選擇LayerNorm（J. L. Ba, Kiros, 和 Hinton，2016）），其靈感來源于RetNet在類似位置使用歸一化層的做法（Y. Sun 等，2023）。

3.5 選擇機制的特性

選擇機制是一個更廣泛的概念，可以以不同的方式應用，例如應用于更傳統的RNN或CNN，或者應用于不同的參數（例如算法2中的𝑨），或者使用不同的變換𝑠(𝑥)。

3.5.1 與門控機制的關系

我們強調最重要的關系：RNN的經典門控機制是我們為SSM設計的選擇機制的一個實例。我們注意到，RNN門控與連續時間系統離散化之間的聯系是非常明確的（Funahashi 和 Nakamura，1993；Tallec 和 Ollivier，2018）。實際上，定理1是對Gu, Johnson, Goel等（2021年，第3.1引理）的改進，擴展到了ZOH離散化和輸入依賴門控（證明見附錄C）。更廣泛地說，SSM中的Δ可以看作是RNN門控機制的廣義版本。根據以往的研究，我們采納了將SSM離散化視為啟發式門控機制的理論基礎的觀點。

定理 1. 當 𝑁 = 1，𝑨 = ?1，𝑩 = 1，𝑠Δ = Linear(𝑥)，且 𝜏Δ = softplus 時，選擇性SSM的遞歸（算法2）可以表示為：

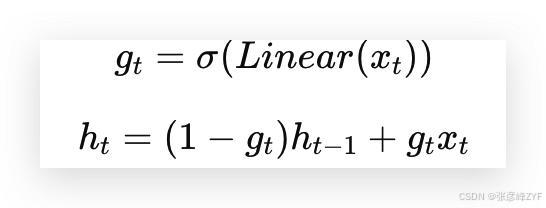
如第3.2節所述，我們對𝑠Δ、𝜏Δ的具體選擇正是基于這一聯系。特別地，請注意，如果給定的輸入𝑥𝑡應該被完全忽略（如在合成任務中所需），所有𝐷個通道都應忽略該輸入，因此我們會將輸入投影到1維，然后再用Δ進行重復/廣播。

3.5.2 選擇機制的解釋

我們闡述了選擇機制的三個特定機制效應。

可變間隔
選擇性允許過濾掉可能出現在感興趣的輸入之間的無關噪聲標記。這在選擇性復制任務中有所體現，但在常見的數據模態中普遍存在，特別是對于離散數據——例如，語言填充詞如“呃”。這一特性出現的原因是，模型可以機械地過濾掉任何特定的輸入𝑥𝑡，舉例來說，在門控RNN的情況下（定理1）當𝑔𝑡 → 0時。

過濾上下文
有實驗證明，盡管更多的上下文應該嚴格提升性能，但許多序列模型在增加上下文長度時并未改善性能（F. Shi等，2023）。一個解釋是，許多序列模型在必要時無法有效地忽略無關的上下文；一個直觀的例子是全局卷積（以及一般的LTI模型）。另一方面，選擇性模型可以隨時重置其狀態，以去除多余的歷史信息，因此從原則上講，隨著上下文長度的增加，它們的性能會單調改善（例如，第4.3.2節）。

邊界重置
在多個獨立序列拼接在一起的設置中，Transformer可以通過實例化特定的注意力掩碼來保持它們的獨立性，而LTI模型則會在序列之間泄漏信息。選擇性SSM也可以在邊界處重置其狀態（例如，Δ𝑡 → ∞，或者定理1中當𝑔𝑡 → 1時）。這些設置可能是人為的（例如，為了提高硬件利用率而將文檔打包在一起），也可能是自然的（例如，強化學習中的episode邊界（Lu等，2023））。

此外，我們還詳細闡述了每個選擇性參數的效應。

Δ的解釋
通常，Δ控制著在多大程度上聚焦或忽略當前的輸入𝑥𝑡。它是RNN門控（例如定理1中的𝑔𝑡）的推廣：從機械角度來看，較大的Δ重置狀態?并專注于當前輸入𝑥，而較小的Δ則保持狀態并忽略當前輸入。SSM（1）和（2）可以被解釋為一個通過時間步長Δ離散化的連續系統，在這個背景下，直覺是大Δ → ∞代表系統長時間關注當前輸入（從而“選擇”它并忘記其當前狀態），而小Δ → 0則代表一個被忽略的瞬時輸入。

𝑨的解釋
我們指出，雖然𝑨參數也可以是選擇性的，但它最終只通過與Δ的交互（通過𝑨 = exp(Δ𝑨)離散化（4））影響模型。因此，Δ的選擇性足以確保(𝑨, 𝑩)的選擇性，并且是主要的改進來源。我們假設使𝑨具有選擇性，除了（或代替）Δ，也會有類似的性能，因此為了簡便，我們沒有包含這一部分。

𝑩和𝑪的解釋
如第3.1節所討論的，選擇性最重要的特性是過濾掉無關信息，以便將序列模型的上下文壓縮成一個高效的狀態。在SSM中，將𝑩和𝑪修改為選擇性可以更精細地控制是否將輸入𝑥𝑡傳遞到狀態?𝑡中，或將狀態傳遞到輸出𝑦𝑡中。這可以解釋為，模型根據內容（輸入）和上下文（隱藏狀態）分別調節遞歸動態。

3.6 其他模型細節

實數與復數
大多數先前的SSM使用復數作為狀態?的一部分，這是在許多感知模態（例如音頻、視頻）中實現良好性能所必需的（Gu, Goel, 和 Ré 2022）。然而，有實驗證明，在某些設置中，完全實值的SSM似乎也能很好地工作，甚至表現得更好（Ma et al. 2023）。我們默認使用實數值，這在除一個任務外的所有任務中都表現良好；我們假設復數和實數的權衡與數據模態中的連續-離散譜有關，其中復數對于連續模態（例如音頻、視頻）有幫助，但對于離散模態（例如文本、DNA）則沒有。

初始化
大多數先前的SSM還建議使用特殊的初始化，特別是在復數值的情況下，這在低數據的情況下有助于提高模型表現。我們在復數情況下的默認初始化是S4D-Lin，在實數情況下是S4D-Real（Gu, Gupta等，2022），這些初始化基于HIPPO理論（Gu, Dao等，2020）。這些初始化將𝑨的第𝑛個元素定義為 ?1/2 + 𝑛𝑖 和 ?(𝑛 + 1)，分別適用于復數和實數情況。然而，我們預計在大數據和實值SSM的情況下，許多初始化方法都能正常工作；一些消融實驗將在第4.6節討論。

Δ的參數化
我們將Δ的選擇性調整定義為𝑠Δ(𝑥) = Broadcast𝐷 (Linear1 (𝑥))，這基于Δ的機械原理（第3.5節）。我們觀察到，這可以從維度1推廣到更大的維度R。我們將其設置為D的一個小分數，這與塊中的主要線性投影相比使用了極少量的參數。我們還注意到，廣播操作可以被視為另一種線性投影，初始化為特定的1和0的模式；如果這個投影是可訓練的，那么它會導致替代的𝑠Δ(𝑥) = Linear𝐷 (Linear𝑅 (𝑥))，這可以視為一個低秩投影。

在我們的實驗中，Δ參數（可以視為偏置項）初始化為

遵循先前在SSM中的工作（Gu, Johnson, Timalsina等，2023）。

備注 3.1
為了簡便起見，在我們的實驗結果中，我們有時將選擇性SSM簡寫為S6模型，因為它們是帶有選擇機制并通過掃描計算的S4模型。

4. 實證評估

在第4.1節中，我們測試了Mamba解決第3.1節中提出的兩個人工任務的能力。隨后，我們在三個領域進行了評估，每個領域都進行了自回歸預訓練以及下游任務的評估。

• 第4.2節：語言模型預訓練（規模法則），以及零-shot下游評估。

• 第4.3節：DNA序列預訓練，并在長序列分類任務上進行微調。

• 第4.4節：音頻波形預訓練，以及自回歸生成的語音片段的質量。

最后，第4.5節展示了Mamba在訓練和推理時的計算效率，第4.6節則對架構和選擇性SSM的各個組件進行了消融實驗。

4.1 人工任務

這些任務的完整實驗細節，包括任務細節和訓練協議，見附錄E.1。

4.1.1 選擇性復制任務

復制任務是最為研究的序列建模任務之一，最初是為測試遞歸模型的記憶能力而設計的。如第3.1節所討論，LTI（線性遞歸和全局卷積）SSM可以輕松解決這個任務，通過僅僅跟蹤時間，而不是考慮數據內容；例如，通過構建一個恰到好處的卷積核（見圖2）。這一點在早期的全局卷積工作中得到了明確驗證（Romero等，2021）。選擇性復制任務通過隨機化標記之間的間距來防止這種簡化方案。注意，這個任務之前已作為去噪任務（Jing等，2019）引入。

許多先前的研究認為，添加架構門控（乘性交互）可以賦予模型“數據依賴性”并解決相關任務（Dao, Fu, Saab等，2023；Poli等，2023）。然而，我們認為這個解釋在直覺上是不充分的，因為這種門控機制并沒有沿著序列軸進行交互，無法影響標記之間的間距。特別地，架構門控并不是選擇機制的一個實例（見附錄A）。

表1確認了，像H3和Mamba這樣的門控架構只在一定程度上提高了性能，而選擇性機制（將S4修改為S6）輕松地解決了這一任務，尤其是在與這些更強大的架構結合時。

4.1.2 誘導頭任務

誘導頭（Olsson等，2022）是一個簡單的任務，從機制解釋的角度（Elhage等，2021）來看，令人驚訝的是它能預測LLM的上下文學習能力。它要求模型執行聯想回憶和復制：例如，如果模型在序列中看到一個二元組“Harry Potter”，那么下次“Harry”出現在同一序列中時，模型應該能夠通過歷史記錄預測“Potter”。

數據集

我們在誘導頭任務上訓練了一個2層模型，序列長度為256，詞匯表大小為16，這與先前在該任務上的工作（Dao, Fu, Saab等，2023）相當，但序列長度更長。我們還通過在從2^6 = 64到2^20 = 1048576的多個序列長度上進行評估，研究了模型的泛化和外推能力。

模型

根據誘導頭任務的既定工作，我們使用了2層模型，這使得注意力機制能夠從機制上解決誘導頭任務（Olsson等，2022）。我們測試了多頭注意力（8個頭，采用不同的位置信息編碼）和SSM變體。我們為Mamba設置了模型維度𝐷為64，其他模型為128。

結果

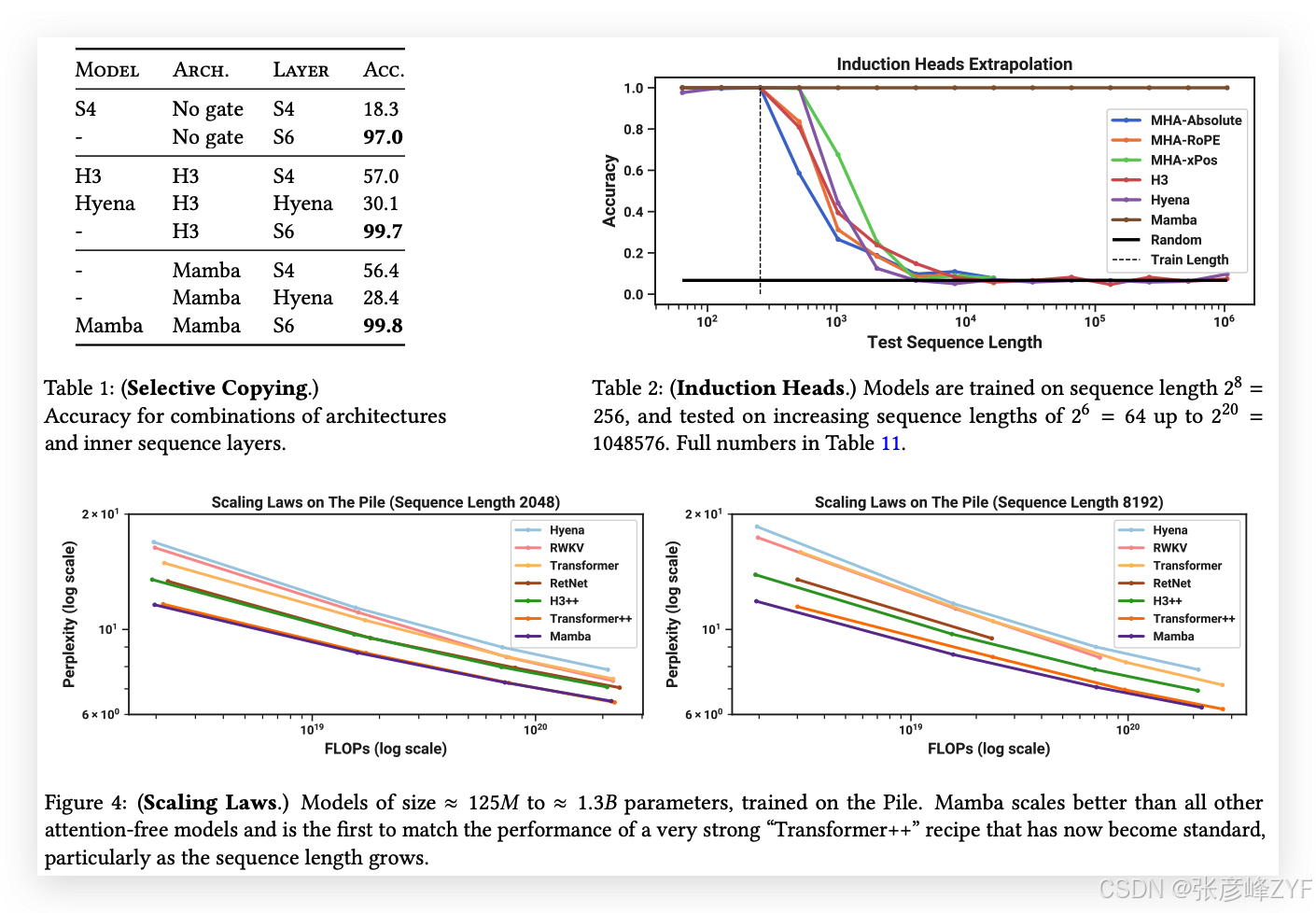
表2顯示，Mamba—或者更準確地說，它的選擇性SSM層—能夠完美地解決這個任務，因為它能夠選擇性地記住相關的標記，同時忽略其間的所有其他內容。它在序列長度達到百萬級時（比訓練時看到的序列長4000倍）完美地泛化，而沒有其他方法能突破2倍的限制。

在所有為注意力模型設計的位置信息編碼變體中，xPos（為長度外推設計）略優于其他變體；同時注意，由于內存限制，所有注意力模型的測試僅限于序列長度2^14 = 16384。與其他SSM相比，H3和Hyena表現相似，這與Poli等（2023）的研究發現相反。

4.2 語言建模

我們在標準的自回歸語言建模任務上評估了Mamba架構，并與其他架構進行了比較，包括預訓練指標（困惑度）和零-shot評估。我們將模型的大小（深度和寬度）設置為與GPT3的規格相匹配。我們使用了Pile數據集（L. Gao, Biderman等，2020），并遵循了Brown等（2020）中描述的訓練方案。所有訓練細節見附錄E.2。

4.2.1 擴展規律

作為基準，我們將Mamba與標準的Transformer架構（GPT3架構）進行比較，并與我們所知的最強Transformer配方（以下簡稱Transformer++）進行比較，該配方基于PaLM和LLaMa架構（例如，旋轉嵌入、SwiGLU MLP、RMSNorm代替LayerNorm、無線性偏置和更高的學習率）。我們還將Mamba與其他最近的次二次架構進行比較（見圖4）。所有模型的詳細信息見附錄E.2。

圖4展示了在標準Chinchilla（Hoffmann等，2022）協議下的擴展規律，模型參數從約125M到約1.3B不等。Mamba是首個在性能上與非常強大的Transformer配方（Transformer++）相匹配的無注意力模型，特別是在序列長度增長時。（我們注意到，由于缺乏高效的實現，RWKV和RetNet基準（之前的強遞歸模型，也可以解釋為SSM）在上下文長度為8k時的完整結果缺失，導致內存不足或不現實的計算需求。）

4.2.2 下游評估

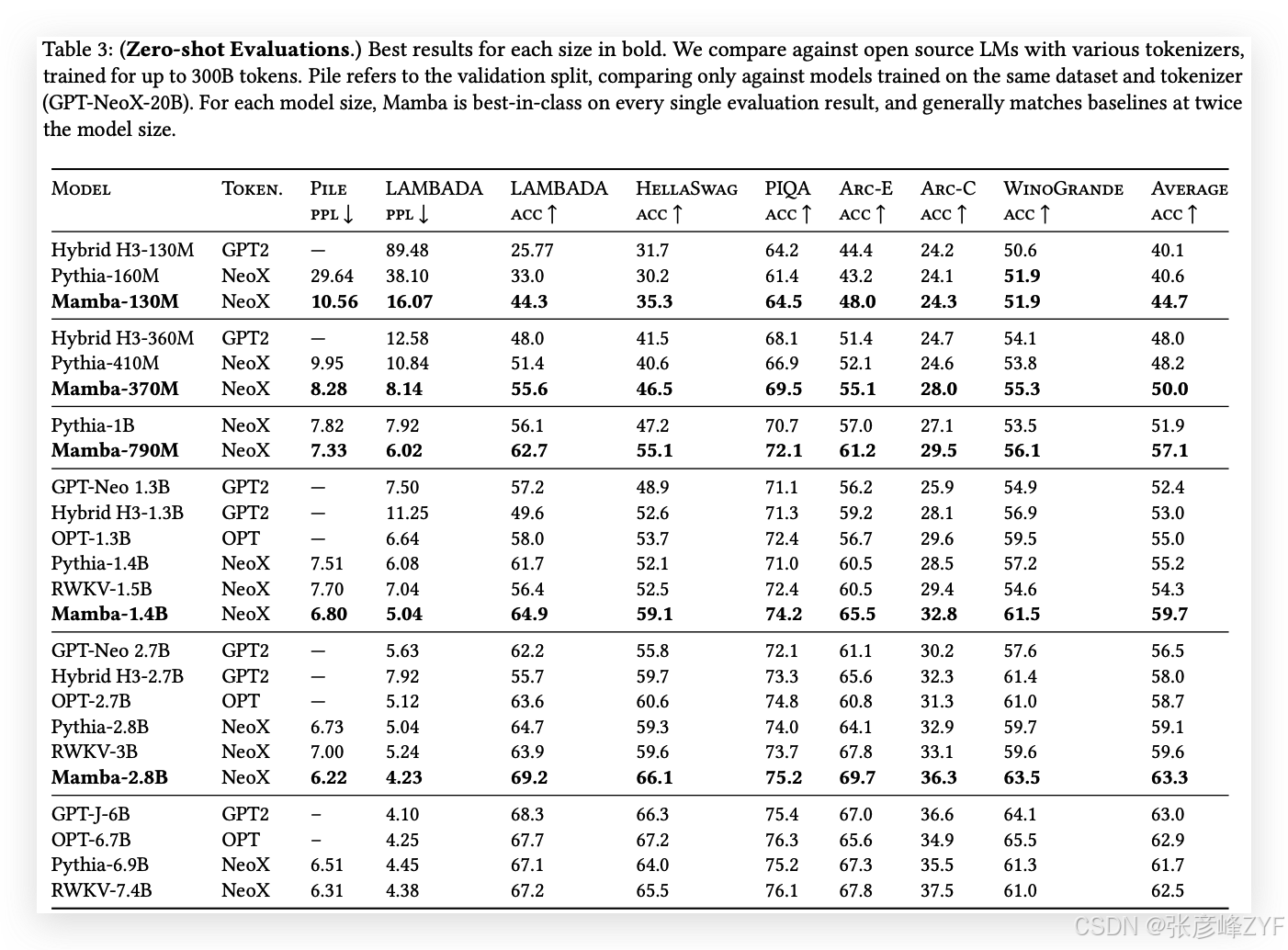
表3展示了Mamba在一系列流行的零-shot下游評估任務中的表現。我們與這些尺寸下最知名的開源模型進行了比較，最重要的是Pythia（Biderman等，2023）和RWKV（B. Peng等，2023），這些模型在與我們的模型相同的分詞器、數據集和訓練長度（300B tokens）上進行訓練。（請注意，Mamba和Pythia的訓練上下文長度為2048，而RWKV的訓練上下文長度為1024。）

4.3 DNA建模

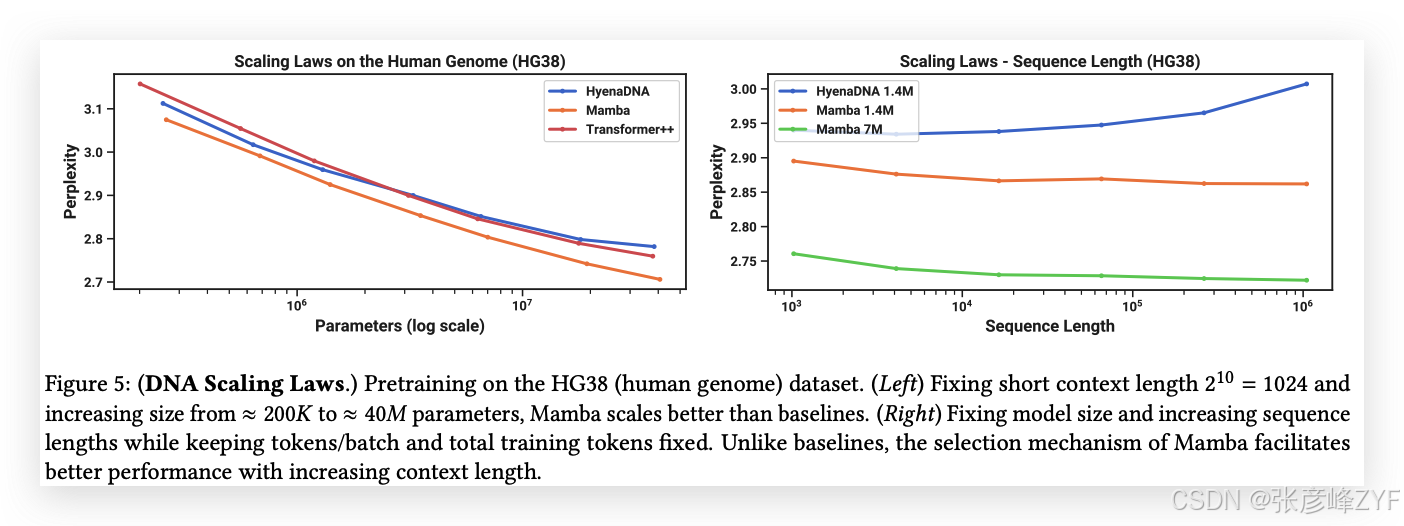
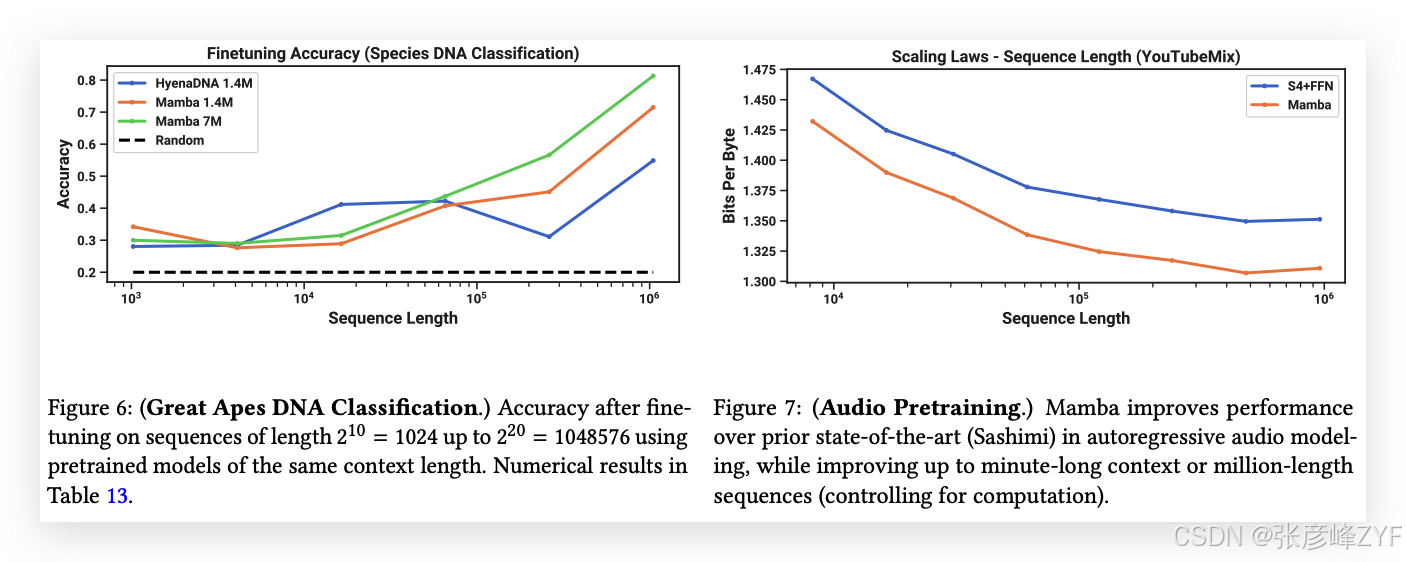
受大規模語言模型成功的啟發，近期研究探索了將基礎模型范式應用于基因組學。DNA被比作語言，因為它由具有有限詞匯的離散符號序列組成。DNA建模還以其需要長程依賴性而著稱（Avsec等，2021）。我們探討了Mamba作為基礎模型（FM）骨干進行預訓練和微調，采用了與最近的DNA長序列模型相關的設置（Nguyen, Poli等，2023）。特別地，我們關注了跨模型大小和序列長度的擴展規律（見圖5），以及一個需要長上下文的困難下游合成分類任務（見圖6）。

在預訓練方面，我們大體遵循標準的因果語言建模（下一個標記預測）設置，訓練和模型細節請參見附錄E.2。對于數據集，我們大致遵循HyenaDNA（Nguyen, Poli等，2023）的設置，該方法使用HG38數據集進行預訓練，該數據集包含一個單一的人類基因組，約有45億個標記（DNA堿基對）用于訓練集。

4.3.1 擴展性：模型大小

在本實驗中，我們研究了基因組基礎模型在不同模型骨干下的擴展性（見圖5左）。

訓練
為了使基線模型受益，我們使用短序列長度1024進行訓練；如4.3.2節所示，我們預計在更長的序列長度下，Mamba的表現將更加突出。我們固定了一個全局批量大小為1024，每個批次大約包含2^20 ≈ 1M個標記。模型訓練了10K梯度步驟，總共使用了10B個標記。

結果
圖5（左）顯示，Mamba的預訓練困惑度隨著模型大小的增加而平穩下降，并且Mamba在擴展性上優于HyenaDNA和Transformer++。例如，在最大的模型大小約40M參數時，曲線顯示Mamba能夠以大約3到4倍更少的參數匹配Transformer++和HyenaDNA模型的表現。

4.3.2 擴展性：上下文長度

在接下來的DNA實驗中，我們研究了模型在序列長度方面的擴展性。我們只比較HyenaDNA和Mamba模型，因為在較長的序列長度下，二次方注意力變得非常昂貴。我們在不同的序列長度上進行預訓練，分別是2^10 = 1024、2^12 = 4096、2^14 = 16384、2^16 = 65536、2^18 = 262144、2^20 = 1048576。我們固定了一個模型大小為6層，每層寬度128（大約1.3M-1.4M參數）。模型訓練了20K梯度步驟，總共使用了大約330B個標記。較長的序列長度采用了與(Nguyen, Poli等，2023)類似的序列長度預熱策略。

結果
圖5（右）顯示，Mamba能夠有效利用更長的上下文，甚至在極長的1M序列長度下，其預訓練困惑度隨著上下文的增加而逐漸下降。另一方面，HyenaDNA模型在序列長度增加時表現變差。這與我們在3.5節中討論的選擇機制屬性是吻合的。特別地，LTI模型不能選擇性地忽略信息；從卷積的角度來看，一個非常長的卷積核會聚合來自長序列的所有信息，而這些信息可能是非常嘈雜的。需要注意的是，盡管HyenaDNA聲稱隨著更長上下文而表現更好，但他們的結果并沒有控制計算時間。

4.3.3 合成物種分類

我們在一個下游任務上評估模型，該任務是通過隨機抽取它們DNA的連續片段對5種不同物種進行分類。這個任務改編自HyenaDNA，后者使用了{人類、狐猴、老鼠、豬、河馬}作為物種集合。我們通過將任務改為在五種大猩猩物種之間進行分類，增加了任務的難度，物種包括{人類、黑猩猩、猩猩、猩紅猩猩、倭黑猩猩}，這些物種已知DNA相似度高達99%。

4.4 音頻建模與生成

對于音頻波形模態，我們主要與SaShiMi架構和訓練協議進行比較（Goel等，2022）。該模型包括：

1. 一個U-Net骨架，具有兩個池化階段，每個階段通過因子𝑝來加倍模型維度𝐷，

2. 在每個階段交替使用S4和MLP塊。

我們考慮將S4+MLP塊替換為Mamba塊。實驗的詳細信息見附錄E.4。

4.4.1 長上下文自回歸預訓練

我們在YouTubeMix數據集（DeepSound，2017）上評估了預訓練質量（自回歸下一個樣本預測），該數據集是一個標準的鋼琴音樂數據集，先前的工作也使用了該數據集，包含4小時的鋼琴獨奏音樂，采樣率為16000 Hz。預訓練的細節大體遵循標準語言建模設置（見4.2節）。圖7評估了將訓練序列長度從2^13 = 8192增加到2^20 ≈ 10^6的影響，同時保持計算量不變。（由于數據整理方式的邊緣情況，可能會導致擴展曲線中出現彎曲。例如，只有一分鐘長的片段可用，因此最大序列長度實際上由60秒·16000Hz = 960000個樣本所限制。）

Mamba和SaShiMi（S4+MLP）基線在更長的上下文長度下均表現出持續改進；Mamba在整個過程中表現更好，且在較長序列長度下差距擴大。主要度量是每字節比特數（BPB），它是標準負對數似然（NLL）損失的常數因子log(2)，用于預訓練其他模態。

我們注意到一個重要細節：這是本文中唯一一個從實數參數化切換到復數參數化的實驗（見3.6節）。我們在附錄E.4中展示了其他消融實驗。

4.4.2 自回歸語音生成

SC09是一個基準語音生成數據集（Donahue，McAuley和Puckette，2019；Warden，2018），包含以16000 Hz采樣的1秒片段，內容是數字“零”到“九”，具有高度可變的特征。我們大體上遵循Goel等（2022）提出的自回歸訓練設置和生成協議。

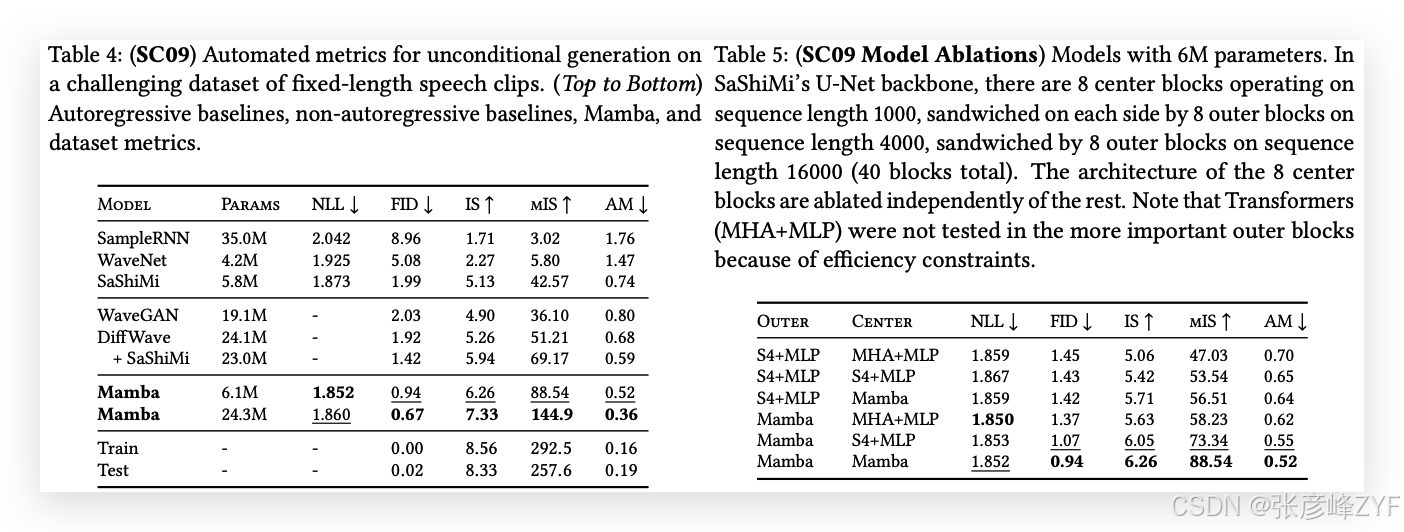
表4展示了Mamba-UNet模型與Goel等（2022）提出的各種基線模型的自動化評估指標：WaveNet（Oord等，2016）、SampleRNN（Mehri等，2017）、WaveGAN（Donahue，McAuley和Puckette，2019）、DiffWave（Z. Kong等，2021）和SaShiMi。一小型Mamba模型超越了最先進的（且更大規模的）GAN和擴散模型。在與基線模型參數相匹配的更大模型中，生成的音頻在保真度指標上得到了顯著提升。

表5以小型Mamba模型為基礎，研究了外部階段和中心階段不同架構的組合。結果顯示，在外部塊中，Mamba始終優于S4+MLP，而在中心塊中，Mamba > S4+MLP > MHA+MLP。

4.5 速度和內存基準測試

我們基準測試了SSM掃描操作（狀態擴展𝑁 = 16）的速度，以及Mamba的端到端推理吞吐量，結果見圖8。

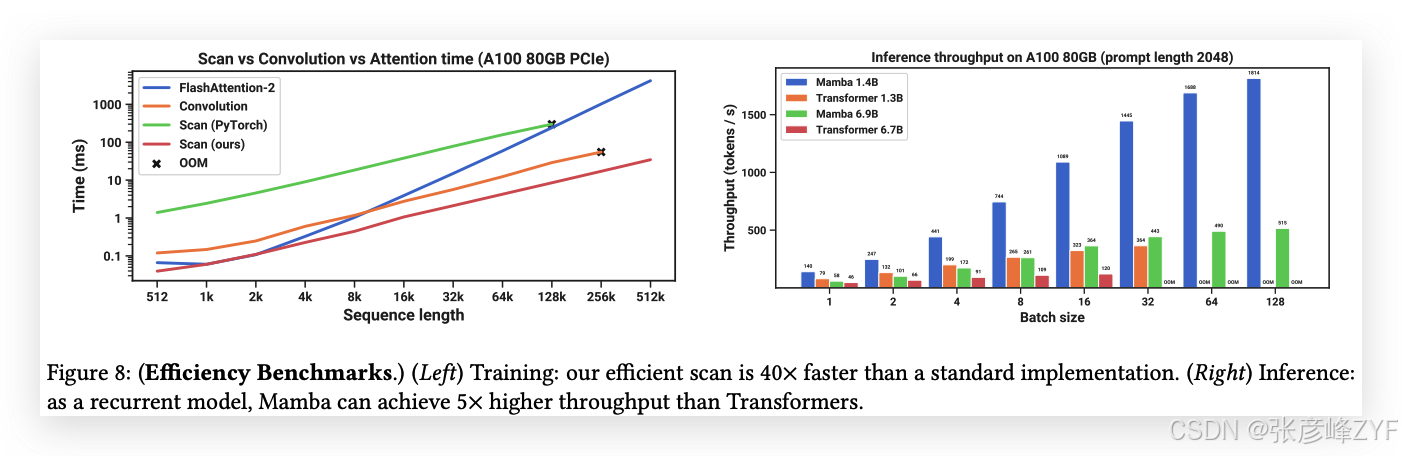
我們的高效SSM掃描在序列長度超過2K時，比我們所知的最佳注意力實現（FlashAttention-2（Dao，2024））更快，且比標準的PyTorch掃描實現快20-40倍。Mamba的推理吞吐量比同等規模的Transformer高出4-5倍，因為它無需KV緩存，能夠使用更大的批次大小。例如，一個6.9B參數的Mamba（未經訓練）在推理吞吐量上將超過一個5倍更小的1.3B參數Transformer。詳細信息見附錄E.5，其中還包括內存消耗的基準測試。

4.6 模型消融實驗

我們對模型的各個組件進行了詳細的消融實驗，重點研究語言建模任務中的設置（模型規模約為350M，使用Chinchilla令牌計數，與圖4相同的設置）。

4.6.1 架構

表6研究了架構（塊）及其內部SSM層（圖3）的效果。我們發現：

• 在之前的非選擇性（LTI）SSM中，這些模型等同于全局卷積，其性能非常相似。

• 將之前工作的復數值S4變體替換為實數值變體對性能影響不大，這表明（至少對于語言建模任務）考慮硬件效率時，實數值SSM可能是更好的選擇。

• 用選擇性SSM（S6）替換這些模型會顯著提高性能，驗證了第3節中的動機。

• Mamba架構的表現與H3架構相似（當使用選擇性層時，似乎略有更好表現）。

我們還研究了將Mamba塊與其他塊（如MLP（傳統架構）、MHA（混合注意力架構））交替使用的情況，詳細信息請參見附錄E.2.2。

4.6.2 選擇性SSM

表7通過考慮選擇性Δ、𝑩和𝑪參數（算法2）的不同組合，消融了選擇性SSM層，結果顯示Δ是最重要的參數，因為它與RNN門控機制（定理1）有關。

表8考慮了SSM的不同初始化，這在某些數據模態和設置中已被證明能產生較大差異（Gu, Goel, 和 Ré 2022；Gu, Gupta 等人 2022）。在語言建模任務中，我們發現較簡單的實數值對角初始化（S4D-Real，第3行）比更常見的復數值參數化（S4D-Lin，第1行）表現更好。隨機初始化也表現良好，這與先前工作的發現一致（Mehta 等人 2023）。

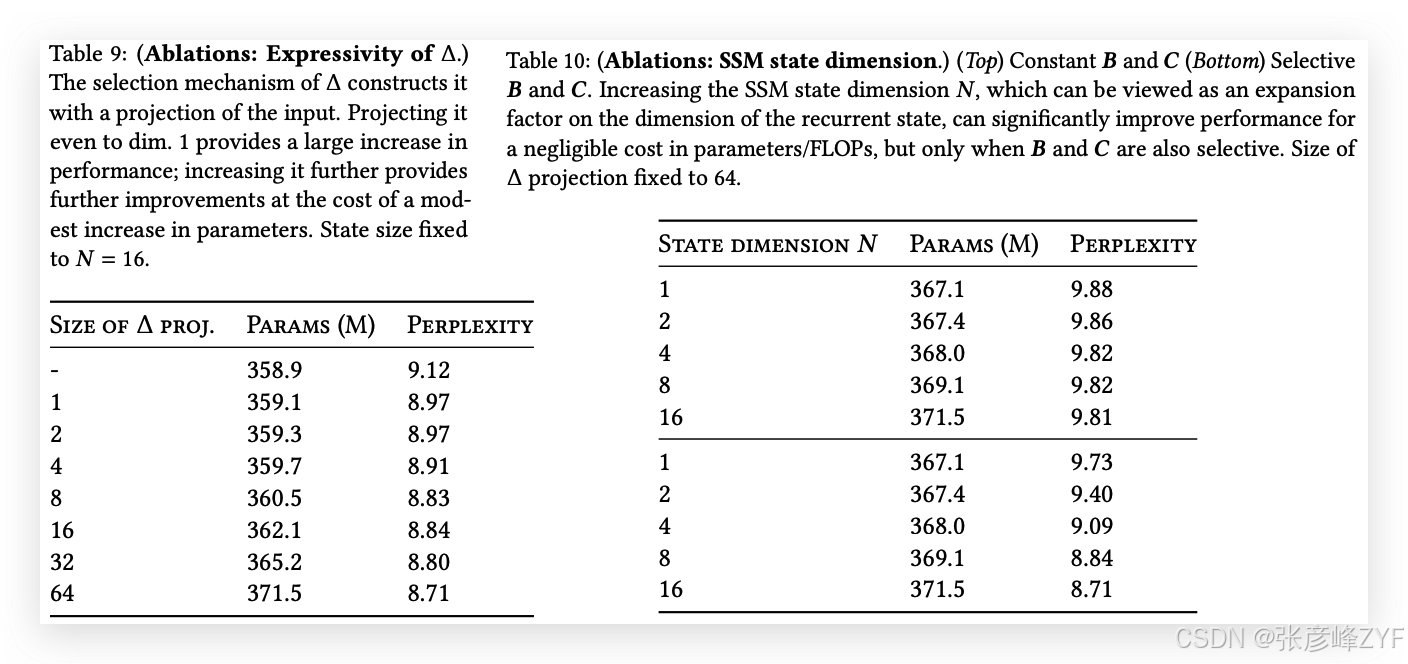
表9和表10分別考慮了Δ和（𝑩，𝑪）投影的維度變化。從靜態到選擇性投影的變化提供了最大的益處，而進一步增加維度通常會略微提高性能，并伴隨著小幅的參數量增加。

特別值得注意的是，當狀態大小𝑁增加時，選擇性SSM表現出顯著改進，在僅增加1%的參數量的情況下，困惑度改善超過1.0。這驗證了我們在第3.1節和第3.3節中的核心動機。

5 討論

我們討論相關工作、局限性以及一些未來的研究方向。

相關工作：附錄A討論了選擇機制與類似概念的關系。附錄B提供了關于SSM和其他相關模型的擴展相關工作。

沒有免費午餐：連續-離散譜：結構化SSM最初被定義為連續系統（1）的離散化，并且在感知信號等連續時間數據模態（例如音頻、視頻）上具有很強的歸納偏置。如第3.1節和第3.5節所討論，選擇機制克服了它們在離散模態（如文本和DNA）中的弱點；但反過來，這可能會妨礙它們在LTI SSM擅長的數據上的表現。我們在音頻波形上的消融實驗更詳細地研究了這一權衡。

下游適配能力：基于Transformer的基礎模型（特別是LLM）具有豐富的屬性和與預訓練模型的交互模式，如微調、適應、提示、上下文學習、指令調優、RLHF、量化等。我們特別感興趣的是，像SSM這樣的Transformer替代品是否具備類似的屬性和適配能力。

擴展：我們的實證評估局限于較小的模型規模，低于大多數強大的開源LLM（例如Llama（Touvron 等人 2023））以及其他遞歸模型如RWKV（B. Peng 等人 2023）和RetNet（Y. Sun 等人 2023）的規模，這些模型已在7B參數及以上的規模上進行評估。仍需評估Mamba在這些更大規模上的表現是否仍然具有優勢。我們還注意到，擴展SSM可能涉及進一步的工程挑戰和模型調整，這些內容在本文中沒有討論。

6 結論

我們向結構化狀態空間模型引入了一種選擇機制，使其能夠在序列長度上線性擴展的同時執行依賴上下文的推理。當該機制被融入一個簡單的無注意力架構時，Mamba在多種領域中達到了最先進的成果，甚至超越了強大的Transformer模型的性能。我們對選擇性狀態空間模型在不同領域中構建基礎模型的廣泛應用感到興奮，尤其是在需要長上下文的創新模態（如基因組學、音頻和視頻）中。我們的結果表明，Mamba是成為通用序列模型骨干的強有力候選者。

致謝

我們感謝Karan Goel、Arjun Desai和Kush Bhatia對草稿的有益反饋。

備注：本文是對《Mamba: Linear-Time Sequence Modeling with Selective State Spaces》為代表的多篇論文的直接翻譯和解讀。