📝前言

在計算機科學的知識體系里，數據結構是構建高效程序與系統的基石，而樹結構，更是其中極具代表性與實用價值的存在。它以獨特的分層組織形式，能高效解決諸如數據檢索、分層管理等各類問題，像文件系統的目錄架構、數據庫的索引設計，都有樹結構的身影 。
掌握樹結構，尤其是二叉樹的概念、不同存儲結構（順序與鏈式 ）及實現，不僅能幫我們理解復雜數據關系的組織邏輯，更能在算法設計、系統優化等實踐中，找到高效解題的鑰匙。接下來，就讓我們深入探索樹結構的奧秘，從基礎概念到具體實現，一步步搭建起對樹結構的清晰認知，為編程能力與問題解決思維的提升，筑牢根基。

🌠樹的概念和結構

🌉樹的概念

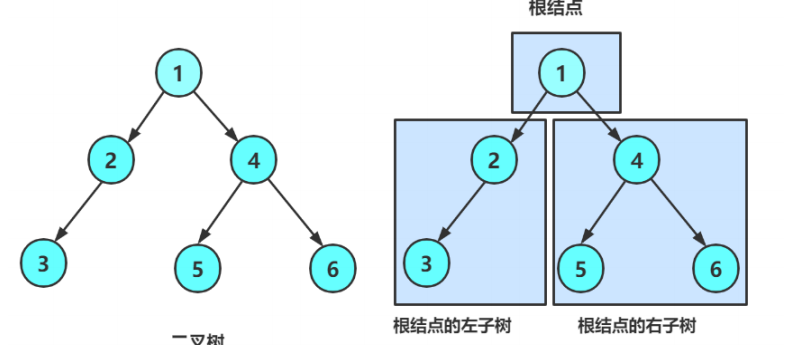
樹是一種非線性的數據結構，有n（n>=0）個有限結點組成的一個有層的集合，他的形狀類似將現實中的樹倒過的模樣，也就是樹根朝上，樹葉朝下。
性質：
1.樹有一個特殊結點，叫根結點，是開端，也就是說根結點前面沒有別的結點了（無前驅結點）。
2.根結點下的接下來的結點又是一顆類似于樹的子樹，它們有且只有一個前驅結點，但可以有0或者多個后繼結點（它不能橫向發展，可以向下發展，要是向上發展有且只有一個結點），因此樹也算是一種遞歸。
3.樹形結構中，子樹之間不能有交集，否則就不是樹形結構。
4.一顆N個結點的樹有N-1條邊。

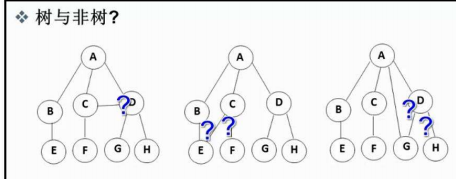
（這里的樹其實可以理解為我們家族的人際關系，這樣就好看待樹相關的性質了。圖片上的都是非樹）

🌉樹的相關概念

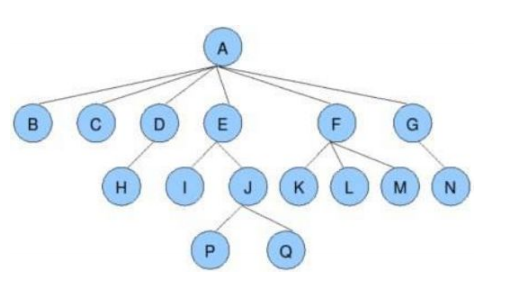
結點的度：一個結點含有的子樹的個數稱為該結點的度； 如上圖：A的為6

葉結點或終端結點：度為0的結點稱為葉結點； 如上圖：B、C、H、I…等結點為葉結點

非終端結點或分支結點：度不為0的結點； 如上圖：D、E、F、G…等結點為分支結點

雙親結點或父結點：若一個結點含有子結點，則這個結點稱為其子結點的父結點； 如上圖：A是B的父結點

孩子結點或子結點：一個結點含有的子樹的根結點稱為該結點的子結點； 如上圖：B是A的孩子結點

兄弟結點：具有相同父結點的結點互稱為兄弟結點； 如上圖：B、C是兄弟結點

樹的度：一棵樹中，最大的結點的度稱為樹的度； 如上圖：樹的度為6

結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推；

樹的高度或深度：樹中結點的最大層次； 如上圖：樹的高度為4

堂兄弟結點：雙親在同一層的結點互為堂兄弟；如上圖：H、I互為兄弟結點

結點的祖先：從根到該結點所經分支上的所有結點；如上圖：A是所有結點的祖先

子孫：以某結點為根的子樹中任一結點都稱為該節點的子孫。如上圖：所有結點都是A的子孫

森林：由m（m>0）棵互不相交的樹的集合稱為森林。

（這里的名稱其實可以理解為我們家族的人際關系，這樣就好看待樹一些的名稱了）用前面的思想理解后 ，我們還要在這里了解：度，層次，高度或深度。

度：其實就是一個結點下連著幾個結點（而這連著的結點下還連著的結點不算）

層次：可以理解為輩分的層次。從最先開始的最高輩（根結點）叫做第一層。

高度或深度：你可以從根結點連接到終端結點，每次連一個，看這條線上有幾個結點，就有多大的高度或深度。

🌉樹的表示

樹的表示有很多種：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。這些方法都是為了要滿足樹既要保存值域，又要保存結點和結點則之間的關系。
孩子兄弟表示法（代碼）：

typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一個孩子結點（靠左邊的孩子結點）struct Node* _pNextBrother; // 指向其下一個兄弟結點DataType _data; // 結點中的值域
};

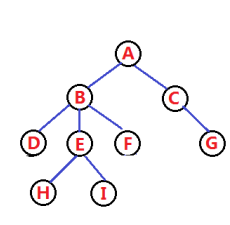
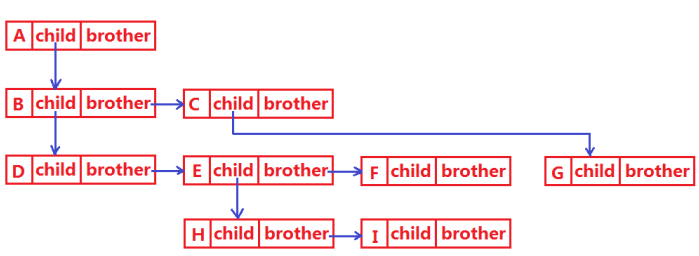
樹的實際應用是在我們的文件系統的目錄結構里面使用。

🌠二叉樹概念及結構

🌉二叉樹的概念

二叉樹是樹的一種特殊情況，就像，在我國的二胎政策下每一家只能生兩個小孩，我們的每一個父結點下最多自能有兩個孩子結點，且最好是將先來為左結點，后至為右結點。因此二叉樹也是一個有序樹。

🌉特殊的二叉樹

1. 滿二叉樹：若二叉樹每一層的結點數都達到該層能容納的最大值，則為滿二叉樹。
   設層數為 K，滿二叉樹的結點總數滿足公式 (2^K - 1)（推導：第 1 層 1 個，第 2 層 2 個…… 第 K 層 (2^{K-1}) 個，總數為等比數列求和 (2^K - 1) ）。當二叉樹結點總數符合此公式時，即為滿二叉樹。
2. 完全二叉樹：完全二叉樹是基于滿二叉樹衍生的高效結構，核心規則為：對深度為 K、含 n 個結點的二叉樹，若其所有結點能與 “深度 K 的滿二叉樹” 中編號 1 到 n 的結點一一對應（可理解為按層序 “填充滿” 滿二叉樹的前 n 個位置 ），則稱為完全二叉樹。
   
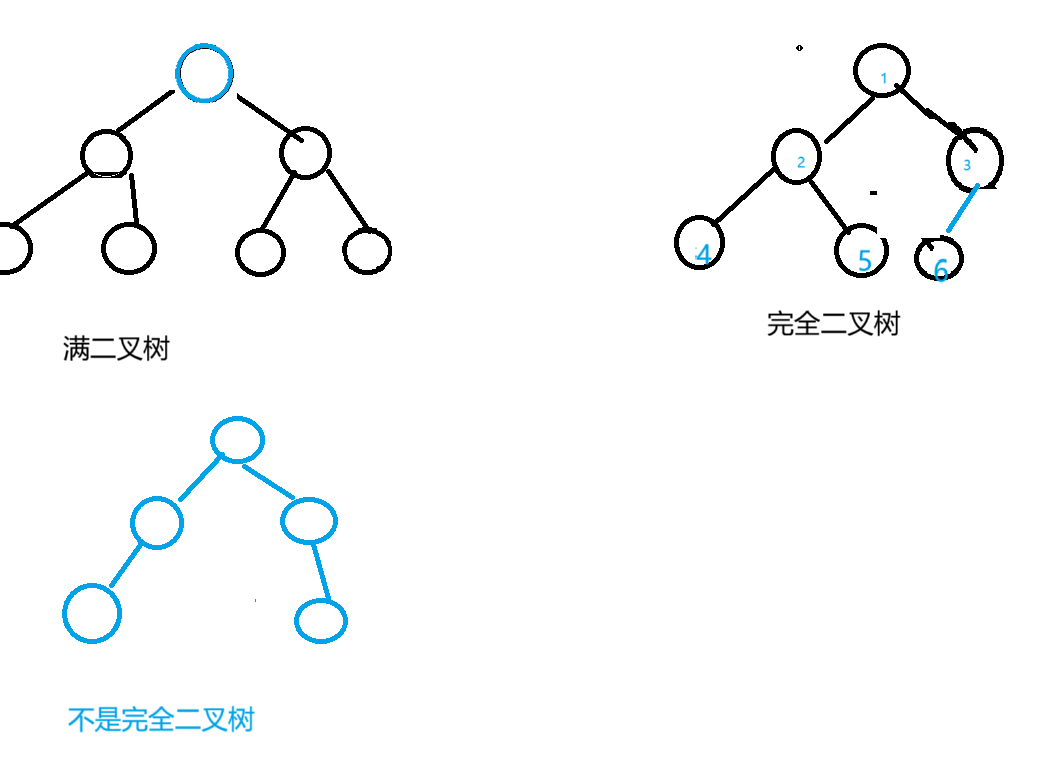
   完全二叉樹得 “從左到右擠著排，不能跳位。

🌉二叉樹的性質

一、層與結點數量關系（根層數為 1 ）
1.第 i 層最多結點數：
非空二叉樹第 i 層，最多有 2^(i - 1)個結點（每一層結點數呈 2 的冪次增長 ）。
2.深度 h 的最大結點數（滿二叉樹場景 ）：
深度為 h 的二叉樹，結點總數最多是 2^h - 1（滿二叉樹時達到此最大值，每層結點數都 “拉滿” ）。

二、葉結點與分支結點的數量關系
對任意二叉樹，記：
No：度為 0 的葉結點個數（無分支的 “末端” 結點 ）
N2：度為 2 的分支結點個數（有兩個子結點的結點 ）
則恒有 No = N2 + 1（葉結點比度 2 結點多 1 ，可通過 “邊數 = 結點數 - 1” 推導 ）。

三、滿二叉樹的深度計算（根層數為 1 ）
若滿二叉樹有 n 個結點，其深度 h 滿足：h = log_2(n + 1)（因滿二叉樹結點數 n = 2^h - 1，變形可得深度公式）。

四、完全二叉樹的編號與親屬結點關系（編號從 0 開始 ）
對有 n 個結點的完全二叉樹，按層序（從上到下、從左到右 ） 編號（根為 0 ），
序號為 i 的結點：
1.雙親結點：若 i>0，雙親序號為 (i-1)/2（整數除法，向下取整 ）；i = 0 是根，無雙親。
2.左孩子：若 2i + 1 < n，左孩子序號為 2i + 1；否則無左孩子。
3.右孩子：若 2i + 2 < n，右孩子序號為 2i + 2；否則無右孩子。

🌠二叉樹順序結構及實現

🌉二叉樹的順序結構

順序結構存儲就是使用數組來存儲，一般使用數組只適合表示完全二叉樹，因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲。二叉樹順序存儲在物理上是一個數組，在邏輯上是一顆二叉樹。

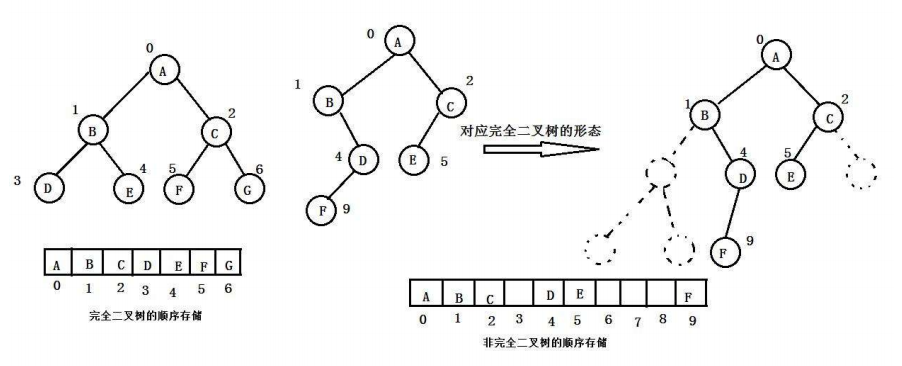
按照圖上的情況，非完全二叉樹會有空間浪費和操作復雜度高以及結構表達不直觀的劣勢。所以順序結構還是用完全二叉樹的好。

🌉堆的概念及結構

現實中我們通常把堆(一種二叉樹)使用順序結構的數組來存儲，需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事，一個是數據結構，一個是操作系統中管理內存的一塊區域分段。

一 堆的定義
給定關鍵碼集合 K = {k0, k1, k2, …, k（n-1）}，按完全二叉樹的順序存儲方式（即層序存儲到一維數組 ）存放，且滿足以下關系之一：
小根堆（小堆）：對任意下標 i，有 Ki <= K(2i+1) 且 Ki <= K(2i+2)（父結點值 ≤ 左右子結點值 ）。
大根堆（大堆）：對任意下標 i，有 Ki <= K(2i+1) 且 Ki >= K(2i+2)（父結點值 ≥ 左右子結點值 ）。

若根結點是堆中最小元素 → 小根堆；若根結點是堆中最大元素 → 大根堆。

二、堆的性質
1.結點值的層級關系：堆中任意結點的值，總是不大于（小根堆）或不小于（大根堆）其父結點的值，保證根結點是堆的 “極值”（最小 / 最大 ）。
2.結構特征：堆一定是完全二叉樹（存儲方式和規則決定，結點按層序填充，無 “跳位” ）。

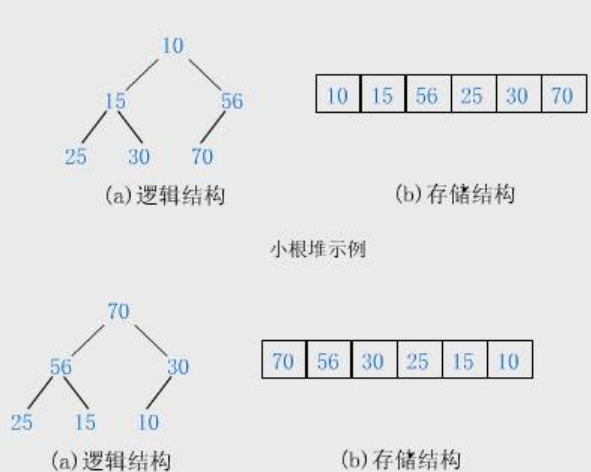
第一個是小根堆，第二個是大根堆。

🌉堆的實現

堆的聲明：

typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity; 
}Heap;
// 堆的構建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
HPDataType HeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

接下來我們要逐步學習堆的知識。

🍁堆向下調整算法

先定義一個數組，這個數組從邏輯上看是一顆完全二叉樹。我們從根結點開始向下調整算法，將其調整一個小堆。但有一個條件：左右子樹必須是一個堆，才能調整。

int array[] = {27,15,19,18,28,34,65,49,25,37};

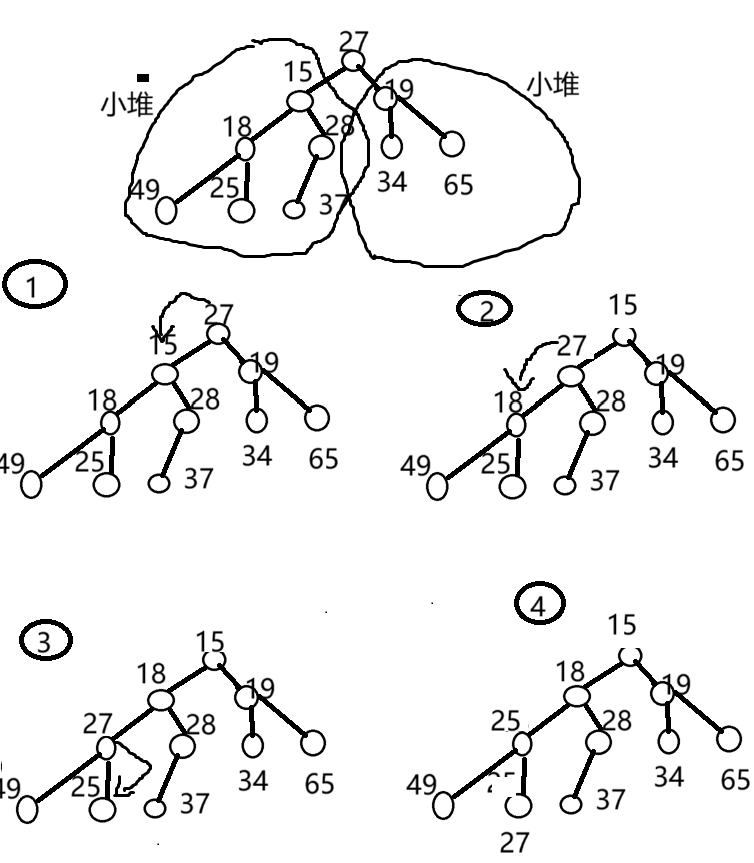
以27為根的左右子樹，都滿足小堆的性質，只有根節點不滿足，因此只需將根節點往下調整到合適的位置即可形成堆。

🍁堆的創建

構建堆時，從最后一個非葉子節點的子樹開始，向上調整到根，把完全二叉樹數組改成堆 。

定義一個數組：

int a[] = {1,5,3,8,7,6};

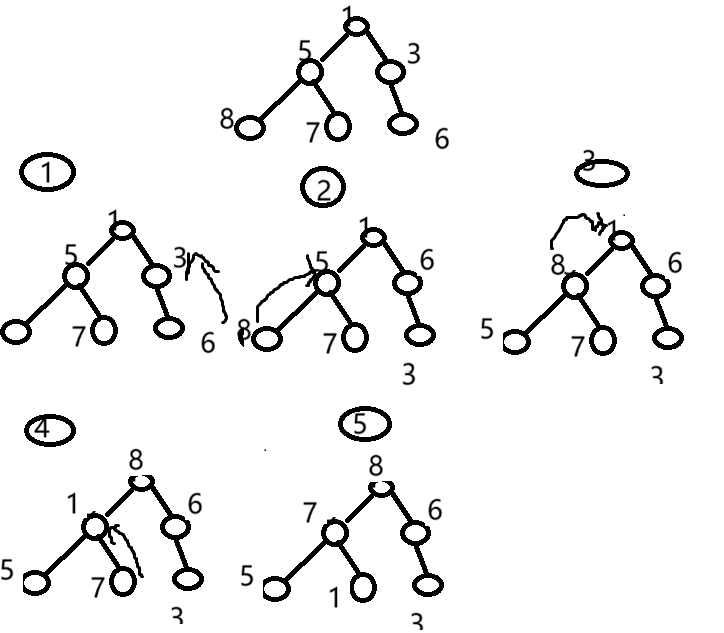
第3步：此時調換 1 和 8 的位置的時候，8 的其左子樹構成的歸結結構被破壞。如第3步8下面的左子樹。因此，每一次調換元素的時候，有可能破壞其子堆的結構。

因此，每一次發生元素交換的時候，都需要遞歸調用重新構造堆的結構。此時就要重新對這一部分進行重新構造堆。

🍁建堆的時間復雜度

前提：因堆是完全二叉樹，為便于分析，用滿二叉樹（屬完全二叉樹）推導，少量節點不影響最終近似結果。

分層分析：設樹高為 h，按層統計節點數與移動步數：第 i 層（從 0 開始）有 2^i 個節點，需向下移動 h - i - 1 層（如第 1 層節點移動 h - 2 步 ）。

第 1 層，2^0個節點，需要向下移動h - 1層
第 2 層，2^1個節點，需要向下移動h - 2層
第3 層 ，2^2個節點，需要向下移動h - 3層
第 4 層，2^3個節點，需要向下移動h - 4層
……
第h - 1層，2^{h - 2}個節點，需要向下移動 1 層

公式構建：總移動步數 T(n)按層累加，得到含等比數列的表達式 ①；通過構造 2*T(n) 并與 ① 錯位相減，化簡后結合滿二叉樹節點數 n = 2^h - 1（即 h = log_2(n + 1)，最終推導出 T(n)約等于n 。

結論：建堆時間復雜度為 O(N) ，體現建堆操作隨數據規模增長，時間成本線性遞增的特性。

🍁堆的插入

1.先將元素插入到堆的末尾，即最后一個葉子之后
2.插入之后如果堆的性質遭到破壞，將新插入節點順著其雙親往上調整到合適位置即可
3.簡而言之：就是進行向上調整算法，直到滿足堆

🍁堆的刪除

刪除堆是刪除堆頂的數據，將堆頂的數據根與最后一個數據一換，然后刪除數組最后一個數據，再進行向下調整算法。

🌉堆的應用

🍁堆排序

1. 建堆
   升序：建大堆
   降序：建小堆

2. 利用堆刪除思想來進行排序

3. 建堆和堆刪除中都用到了向下調整，因此掌握了向下調整，就可以完成堆排序。

建堆是針對無序二叉樹（通常基于數組模擬完全二叉樹結構 ）的調整過程，目的是構建大頂堆或小頂堆：
從最后一個非葉子節點開始，
1.若構建大頂堆，比較父節點與子節點值，若父節點小于子節點，選子節點中值最大的與父節點交換；
2.若構建小頂堆，則選子節點中值最小的交換。按此規則，逐層向上對每個子樹遞歸 / 循環調整，使整棵樹滿足堆的有序性（大頂堆父節點≥子節點，小頂堆父節點≤子節點 ）。

堆刪除排序（堆排序核心步驟 ）

基于堆 “根節點為最值（大頂堆最大、小頂堆最小 ）” 的性質：
1.若根節點不滿足最值，先通過向下調整讓根節點成為最值 。

2.將根節點（最值 ）與堆最后一個數據交換，把最值 “固定” 到堆末尾 。

3.對剩余未固定的堆結構（除末尾已交換元素 ），再次執行向下調整，恢復堆性質。重復此過程，最終完成排序，使數據按升序（大頂堆場景 ）或降序（小頂堆場景 ）排列 。

🍁TOP-K問題

TOP - K 問題是從大規模數據里找前 K 個最大或最小元素，因數據量大排序法受限，用堆解決更優，步驟為：
1.建堆：找最大元素建小堆，找最小元素建大堆，用前 K 個元素初始化堆。

2.篩選：剩余 N - K 個元素逐個與堆頂比，不滿足條件（如找最大時堆頂小則替換 ）就替換堆頂，調整堆結構。

3.結果：處理完后，堆里 K 個元素就是前 K 個最大或最小元素，利用堆的特性高效篩選，適配大數據場景 。

舉個🌰（找前 3 大的元素）：

數據是 [5, 3, 8, 1, 9, 2, 7]，K=3。
目標：找最大的 3 個（8、9、7）。

1. 第一步：先拿前 3 個 [5, 3, 8] 建 小頂堆，堆頂是 3（小頂堆特性：堆頂最小）。

2. 第二步：“篩選 → 用篩子過濾數據”
   剩下的數據（除了前 K 個），逐個和 堆頂 比較：
   如果比堆頂 “更優”（找最大時，比堆頂大；找最小時，比堆頂小）→ 替換堆頂，再調整堆結構（保持堆的規則）；如果不如堆頂 → 直接淘汰，不管它。

接著上面的🌰：
剩余數據是 [1, 9, 2, 7]，堆頂是 3（小頂堆）。
拿 1 和堆頂 3 比：1 < 3 → 淘汰；

拿 9 和堆頂 3 比：9 > 3 → 替換堆頂，堆變成 [5, 8, 9]（調整后小頂堆堆頂回到最小，比如變成 5 ）；

拿 2 和堆頂 5 比：2 < 5 → 淘汰；

拿 7 和堆頂 5 比：7 > 5 → 替換堆頂，堆變成 [7, 8, 9]（調整后堆頂是 7 ）。

3. 第三步：“結果 → 篩子里剩下的就是答案”
   過濾完所有數據后，堆里剩下的 K 個元素，就是 “前 K 大 / 前 K 小” 的結果！
   上面的🌰最后堆里是 [7, 8, 9] → 剛好是最大的 3 個元素

// 向下調整函數，構建小堆
#include<stdio.h>
void AdjustDown(int* a, int n, int parent) {int child = 2 * parent + 1;while (child < n) {// 找較小的子節點if (child + 1 < n && a[child + 1] < a[child]) {child++;}// 子節點小于父節點，交換并繼續調整if (a[child] < a[parent]) {int temp = a[child];a[child] = a[parent];a[parent] = temp;parent = child;child = 2 * parent + 1;} else {break;}}
}
void PrintTopK(int* a, int n, int k)
{// 1. 建堆--用a中前k個元素建堆for (int i = (k / 2) - 1; i >= 0; i--) {AdjustDown(a, k, i);}// 2. 將剩余n-k個元素依次與堆頂元素交換，不滿則則替換for (int i = k; i < n; i++) {if (a[i] > a[0]) {int temp = a[i];a[i] = a[0];a[0] = temp;AdjustDown(a, k, 0);}}// 這里可按需輸出堆中前 K 個元素，示例簡單打印堆內數據for (int i = 0; i < k; i++) {printf("%d ", a[i]);}printf("\n");
}
void TestTopk()
{int n = 10000;int* a = (int*)malloc(sizeof(int)*n);srand(time(0));for (size_t i = 0; i < n; ++i){a[i] = rand() % 1000000;}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;PrintTopK(int* a, n, 10);
}

🚩總結

感謝你的收看，如果文章有錯誤，可以指出，我不勝感激，讓我們一起學習交流，如果文章可以給你一個小小幫助，可以點一個小小的贊😘