目錄
- 1.摘要
- 2.數學模型
- 3.求解方法
- 4.結果展示
- 5.參考文獻
- 6.代碼獲取
- 7.算法輔導·應用定制·讀者交流

1.摘要
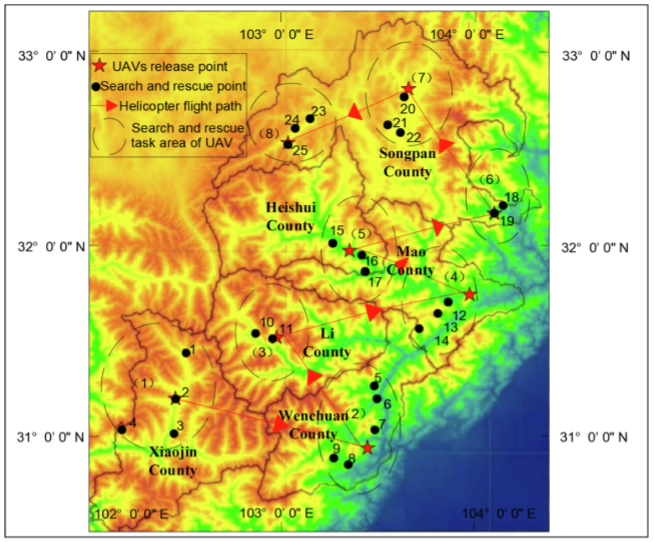
無人機任務分配對于保障搜救活動高效有序開展具有重要意義,但現有研究較少考慮無人機作業環境與性能對任務分配的影響。針對低空風場和地形因素對無人機能耗與性能的影響,本研究提出了直升機釋放位置選擇與任務分配模型。考慮到地形因素會影響無人機探測區域,采用主成分分析法確定各搜救點的搜救等級,并運用聚類分析確定無人機懸停續航能力。結合無人機性能、低空風場等影響電池能耗的因素,構建無人機釋放位置選擇模型,采用改進二進制蝙蝠算法求解。根據釋放位置規劃結果,建立以總搜救成本最小、無人機數量最少及多機任務均衡為目標的優化模型,運用NSGA-II進行求解。
2.數學模型

無人機釋放位置選擇模型
無人機任務分配必須將實際避障能耗納入考量,本研究基于最壞工況假設,建立以下能量管理機制:滿載無人機必須保持2/3能量狀態抵達目標點,并預留1/3能量用于返航。
minZ=∑j∈M∑k∈NczjkSjk+∑j∈MFjxjminZ=\sum_{j\in M}\sum_{k\in N}cz_{jk}S_{jk}+\sum_{j\in M}F_jx_j minZ=j∈M∑?k∈N∑?czjk?Sjk?+j∈M∑?Fj?xj?
無人機搜救任務分配模型
目標函數主要包括三部分,即無人機的搜救成本,以及使用的無人機數量和完成任務所需的總時間。應考慮無人機的任務平衡性和合理性。目標函數要求總成本最小,包括無人機飛行和懸停產生的航程成本,前者與無人機飛行航程能耗成正比,后者與懸停時間成正比。
minZ1=minc(∑k∈K∑i∈P∑j∈Psijyijxijk+∑i∈Nsi)minZ_1=minc\left(\sum_{k\in K}\sum_{i\in P}\sum_{j\in P}s_{ij}y_{ij}x_{ijk}+\sum_{i\in N}s_i\right) minZ1?=minc?k∈K∑?i∈P∑?j∈P∑?sij?yij?xijk?+i∈N∑?si??
無人機的實際數量在實踐中是有限的,因此使用的無人機數量應盡可能低。
minZ2=min∑k∈K∑j∈Px0jkminZ_2=min\sum_{k\in K}\sum_{j\in P}x_{0jk} minZ2?=mink∈K∑?j∈P∑?x0jk?
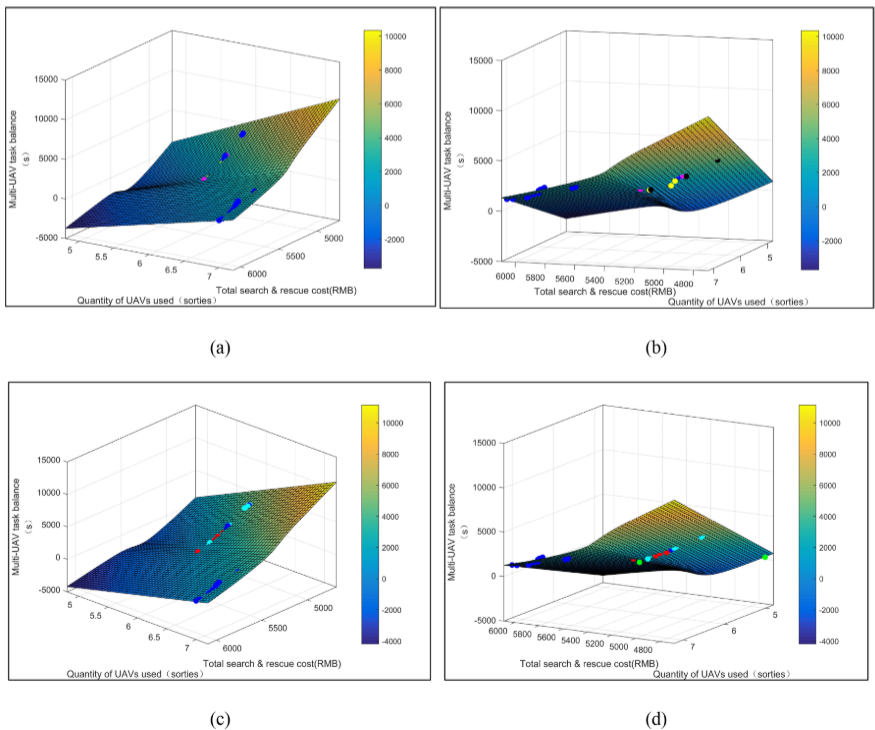
考慮任務平衡性,在考慮成本問題的同時,將不同無人機花費任務的時間最大差異減小到最小。
minZ3=min{Tkmax?Tkmin},Tkmax,Tkmin∈TminZ_3=min\{T_{kmax}-T_{kmin}\},T_{kmax},T_{kmin}\in T minZ3?=min{Tkmax??Tkmin?},Tkmax?,Tkmin?∈T
3.求解方法
主成分分析法對搜救點進行分級

無人機探測盲區算法

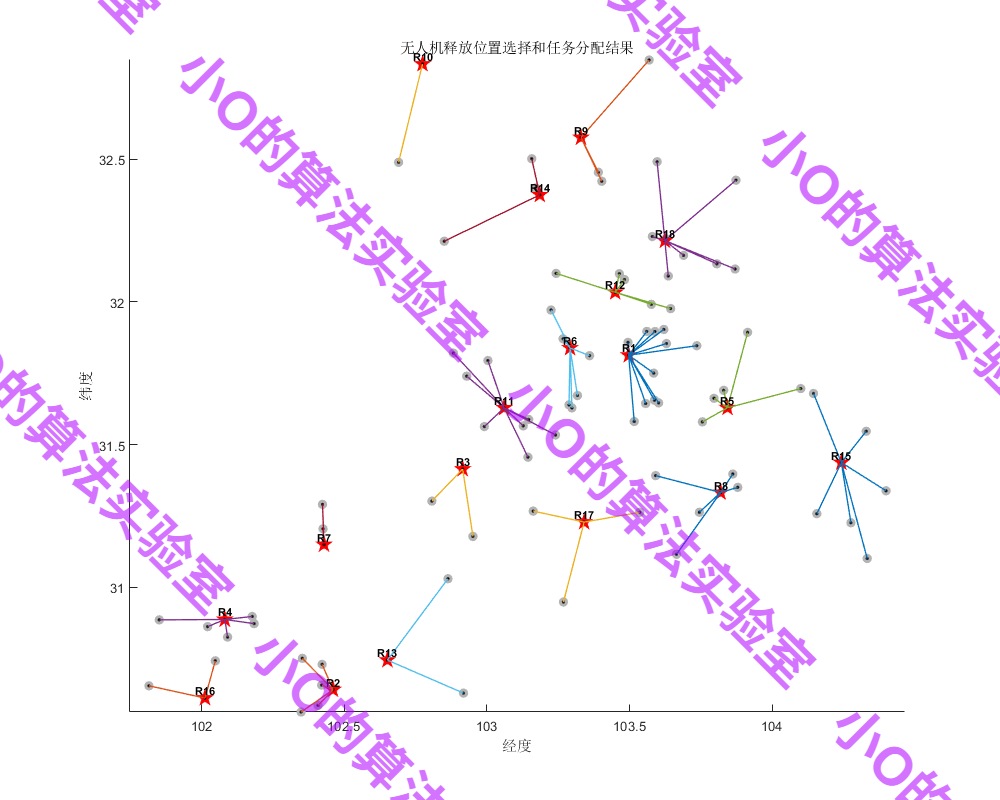
IBBA解決無人機從直升機上的釋放位置


基于NSGA-II的無人機任務分配
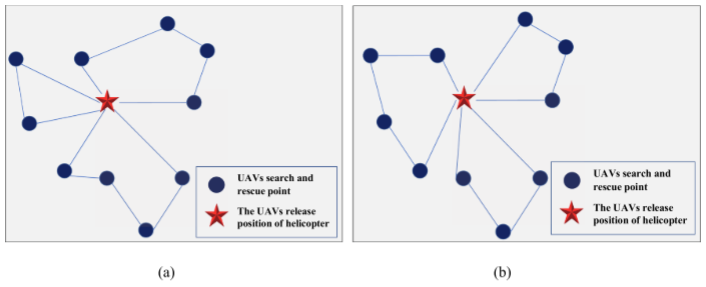
考慮到多無人機任務分配問題的局限性,參考文獻(Wang et al., 2018),采用雙染色體編碼方法進行編碼,其中染色體I表示目標序列,染色體II表示目標序列在I上的切割位置。I上的每個基因表示每個搜索目標的索引,基因總數為NT。任意一個基因的值不得小于其前一個基因的值,基因號為(NU?1)。

NSGA-II采用快速非支配排序,擁擠度比較算子,個體iii的擁擠距離:
L(i)=∑k=13Zk×(L(i+1)?L(i?1))/(Zkmax?Zkmin)L(i)=\sum_{k=1}^3Z_k\times(L(i+1)-L(i-1))/\left(Z_k^{max}-Z_k^{min}\right) L(i)=k=1∑3?Zk?×(L(i+1)?L(i?1))/(Zkmax??Zkmin?)

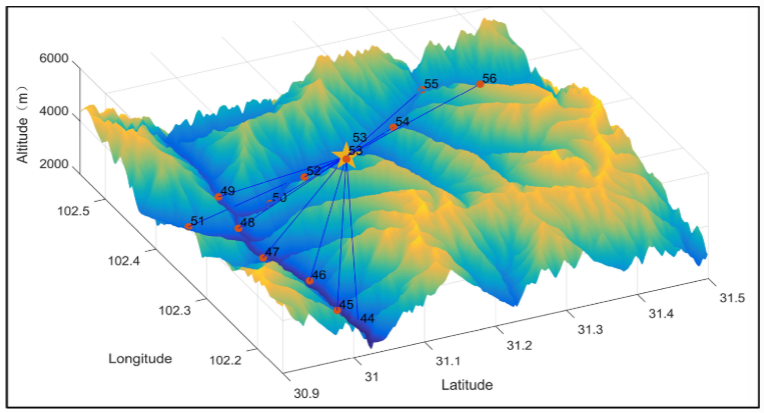
4.結果展示
5.參考文獻
[1] Zhang M, Li W, Wang M, et al. Helicopter–UAVs search and rescue task allocation considering UAVs operating environment and performance[J]. Computers & Industrial Engineering, 2022, 167: 107994.
6.代碼獲取
xx














)



)
