目錄

15.力扣 904.水果成籃

15.1 題目解析：

15.2 算法思路：

15.2.1 暴力解法：

15.2.1 滑動窗口

15.3代碼演示：

15.4 總結反思：

16 力扣 438.找出字符串中所有字母的異位詞

16.1 題目解析：

16.2算法思路：

16.3 代碼實現：

?編輯

16.4 總結反思：

17 力扣 30.串聯所有單詞的子串

17.1 題目解析：

17.2 算法思路：

17.3 代碼演示：

?編輯

17.4 總結反思：

18. 力扣 76。最小覆蓋子串

18.1 題目解析：

18.2 算法思路：

18.2.1 暴力枚舉+哈希表

?編輯18.2.2 優化解法：

18.3 代碼演示：

?18.4 總結反思：

19 力扣 704.二分查找

19.1?題目解析：

?19.2 算法思路：

19.3 代碼演示：

?編輯

19.4 總結反思：

?

?

---

15.力扣 904.水果成籃

15.1 題目解析：

要是單單的看這道題目，確實挺難理解的。不過大家仔細的閱讀一下，基本可以理解意思，我把題目給翻譯了一下：大體的意思可以翻譯為找出一個最長的子數組的長度，子數組中不超過兩種類型的水果。?最后返回收集到的最大的水果的數目。

15.2 算法思路：

15.2.1 暴力解法：

解法一就是暴力解法，就是找出子數組，找出其中最長的即可，其中要用到哈希表來存儲水果出現的種類。（若表中水果超過了2種，則直接不用往里面放了）。

15.2.1 滑動窗口

最主要的還是第二種解法。不過在直到用到滑動窗口做之前，還需要直到為什么要用到滑動窗口？

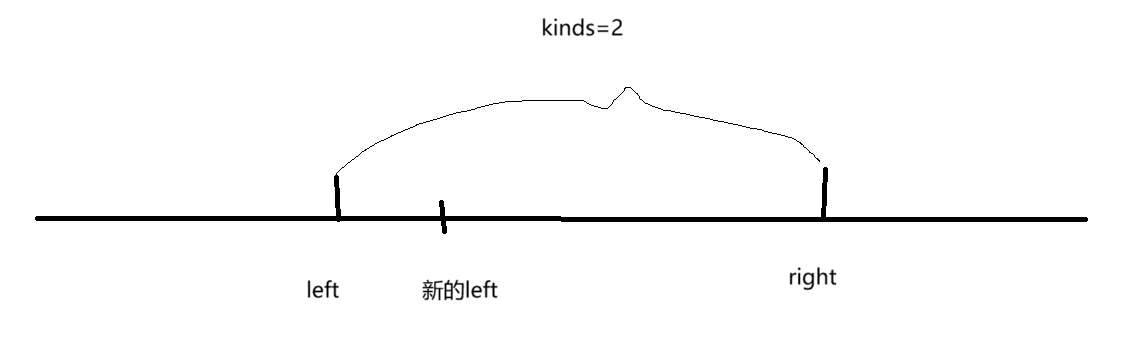
那么大家看著這個圖，我來給大家分析一下。圖中left與right之間是kinds=2，但是如果說left往右挪動一個數字，挪到了新的left的位置，那么請問，kinds的大小會怎么變呢？

1.kinds不變，因為若left與right中間恰好有一種水果有兩個，這不正好抵消了嗎？那么此時right也不變。

2.kinds變小，此時說明，恰好把那種水果給挪走了。那么此時right右移（增加水果的種類）。

所以說，right從圖中的位置開始移動left也一直向右邊移動。所以，他們倆是同向的。既然是同向的，那么也就是會用到滑動窗口。并且這個題也涉及到了子數組。

?所以：

1.left，right都是從0開始的。

2.進窗口：這個就是hash[fruits[right]]++.

3.那么判斷出窗口的標準就是hash的大小大于2.出窗口，出了窗口之后，hash[fruits[left]]--。減完后，還得加一步判斷，如果說你的這個hash[fruits[left]]==0,那么這種水果的數量為0，則要把這種水果從哈希表中給踢出去（種類減一）。之后left才加加。（順序別搞錯了）。因為你left先加加的話，會導致這個位置的水果數量還沒判斷呢。

15.3代碼演示：

1.帶容器：若用hash表的話，你得定義兩個int，即hash<int,int>,第一個int表示哪種水果，第二個int表示這種水果有幾個。并且踢出水果要用hash.erase();

?
//使用哈希表（容器）
int totalFruit(vector<int>& fruits) {unordered_map<int, int> hash; //統計窗?內出現了多少種?果int n = fruits.size();int ret = 0;int left = 0;int right = 0;int kind = 0;for (; right < n; right++){if (hash[fruits[right]] == 0) kind++;//若這種水果的數量為0，則要加入這種水果hash[fruits[right]]++;//增加這種水果的數量while (hash.size() > 2)//出窗口{hash[fruits[left]]--;if (hash[fruits[left]] == 0)hash.erase(fruits[left]);//將這種水果刪除left++;}ret = max(ret, right - left + 1);}return ret;
}
int main()
{vector<int> fruits = { 3,3,3,1,2,1,1,2,3,3,4 };cout << totalFruit(fruits) << endl;return 0;
}?

但是呢，帶容器的嘛，肯定時間復雜度不夠好。所以下面還有一個利用數組來模擬哈希表的寫法：

2.用數組代替哈希，得判斷一下，若數組中這種水果數量為0，則數組中還沒有這種水果，就要++kinds，踢出元素的時候，也是這種水果的數量減到0的時候，才踢出去。

//使用數組模擬哈希表
int totalFruit(vector<int>& fruits) {int hash[100000] = { 0 };//定義哈希數組存放水果int n = fruits.size();int ret = 0;int left = 0;int right = 0;int kind = 0;for (; right < n; right++){if (hash[fruits[right]] == 0) kind++;//若這種水果的數量為0，則要加入這種水果hash[fruits[right]]++;//增加這種水果的數量while (kind > 2)//出窗口{hash[fruits[left]]--;if (hash[fruits[left]] == 0) kind--;//將這種水果刪除left++;}ret = max(ret, right - left + 1);}return ret;
}
int main()
{vector<int> fruits = { 3,3,3,1,2,1,1,2,3,3,4 };cout << totalFruit(fruits) << endl;return 0;
}

15.4 總結反思：

總結下來還是滑動窗口的那些做題方法。

16 力扣 438.找出字符串中所有字母的異位詞

16.1 題目解析：

大家仔細閱讀題目，就可知異位詞是什么。例如：abc，那么abc，acb，bac，bca，cab，cba。均為abc的異位詞。

16.2算法思路：

這個的算法思路比較復雜，細節也比較多。

?

?

以上就是本題算法的所有細節與思路了，還是挺多的。關鍵是不好想。

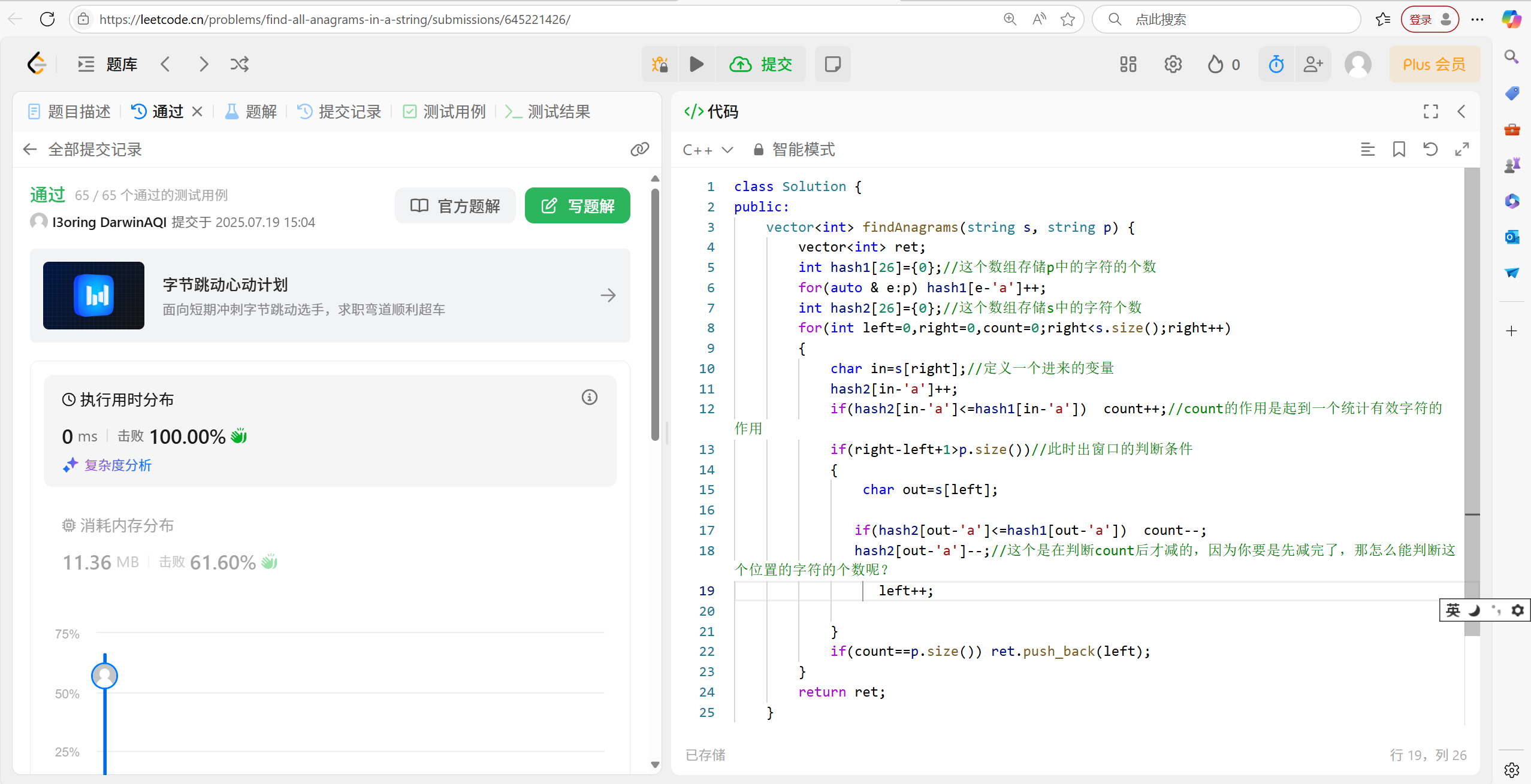
16.3 代碼實現：

//找出字符串中所有字母的異位詞
vector<int> findAnagrams(string s, string p) {vector<int> ret;int hash1[26] = { 0 };//這個數組存儲p中的字符的個數for (auto& e : p) hash1[e - 'a']++;int hash2[26] = { 0 };//這個數組存儲s中的字符個數for (int left = 0, right = 0, count = 0; right < s.size(); right++){char in = s[right];//定義一個進來的變量hash2[in - 'a']++;if (hash2[in - 'a'] <= hash1[in - 'a'])  count++;//count的作用是起到一個統計有效字符的作用if (right - left + 1 > p.size())//此時出窗口的判斷條件{char out = s[left];if (hash2[out - 'a'] <= hash1[out - 'a'])  count--;hash2[out - 'a']--;//這個是在判斷count后才減的，因為你要是先減完了，那怎么能判斷這個位置的字符的個數呢？left++;}if (count == p.size()) ret.push_back(left);}return ret;
}
int main()
{vector<int> outcome;string s("cbaebabacd");string p("abc");outcome = findAnagrams(s, p);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

16.4 總結反思：

本題還是挺有挑戰性的。即使你的思路想出來了，但是如果說你的代碼能力不夠強，也還是寫不出這樣的代碼的。

17 力扣 30.串聯所有單詞的子串

17.1 題目解析：

大家一看到這是個困難題目，好家伙一下子，全蔫了。沒事，不要緊。這道題，你仔細的閱讀一下，是不是跟上一題尋找異位詞差不多，只不過這里的字符變成了字符串。所以本題的解答思路就是，將這些字符串看成字符進行解答。但是細節上呢，可能有些不同。接下來在算法思路里面講解：

17.2 算法思路：

?

本道題目與上一道題目的算法思路幾乎一模一樣，就是一些細節不一樣而已。

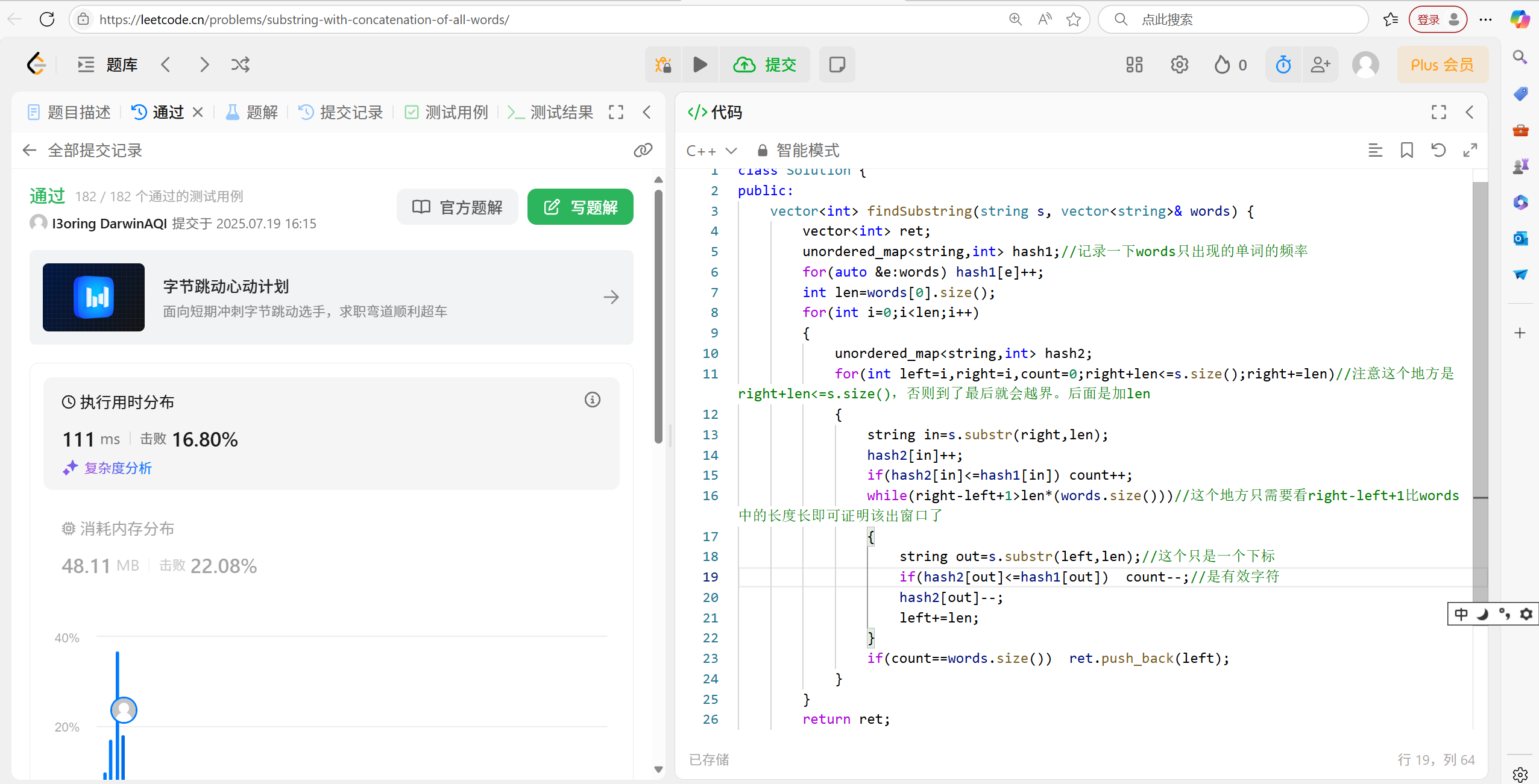
17.3 代碼演示：

//串聯所有單詞的子串
vector<int> findSubstring(string s, vector<string>& words) {vector<int> ret;unordered_map<string, int> hash1;//記錄一下words只出現的單詞的頻率for (auto& e : words) hash1[e]++;int len = words[0].size();for (int i = 0; i < len; i++){unordered_map<string, int> hash2;for (int left = i, right = i, count = 0; right + len <= s.size(); right += len)//注意這個地方是right+len<=s.size()，否則到了最后就會越界。后面是加len{string in = s.substr(right, len);hash2[in]++;if (hash2[in] <= hash1[in]) count++;while (right - left + 1 > len * (words.size()))//這個地方只需要看right-left+1比words中的長度長即可證明該出窗口了{string out = s.substr(left, len);//這個只是一個下標if (hash2[out] <= hash1[out])  count--;//是有效字符hash2[out]--;left += len;}if (count == words.size())  ret.push_back(left);}}return ret;
}
int main()
{string s("barfoothefoobarman");vector<string> words = { "foo","bar" };vector<int> outcome = findSubstring(s, words);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

注意是加len。

17.4 總結反思：

還是得先真正的搞懂一道題目之后，才可以對類似的題目得心應手。

18. 力扣 76。最小覆蓋子串

18.1 題目解析：

題目很短，也很好理解，關鍵就是在于怎么去找出很好的方法去解開這道題。

18.2 算法思路：

18.2.1 暴力枚舉+哈希表

18.2.2 優化解法：

以上便是這道題的全部思路以及細節?，其實還是挺復雜的。

另外還有一些需要注意：

1.能用數組的就用數組，因為數組非常的快（比容器要快）

2.一般，當只有字符的時候，可以用數組，因為字符容易找到下標，就是存儲的位置，且你要是hash[26],那得減去'a',。因為只有26個位置。但要是128的話，就沒必要減了，因為ascii碼表也才127個值

3.字符串只能使用容器（哈希表），因為用數組，無法找到可以存儲的位置。且容器還得有string，int。即unordered_map<string,int>才可以。

18.3 代碼演示：

//最小覆蓋子串
string minWindow(string s, string t) {int hash1[128] = { 0 };int kinds = 0;//統計一下t中的字符的種類有多少for (auto& e : t){if (hash1[e] == 0) kinds++;//如果說這個hash1[e]==0的話，說明暫時沒有這個種類，則需要加上這個種類hash1[e]++;//統計t中的各個字符出現的次數}int hash2[128] = { 0 };int minlen = INT_MAX;int begin = -1;//這個是作為返回字符串的起始位置的beginfor (int left = 0, right = 0, count = 0; right < s.size(); right++){char in = s[right];hash2[in]++;//進窗口if (hash2[in] == hash1[in])  count++;while (count == kinds){if (right - left + 1 < minlen) //這個就是取出最小的長度的符合要求的字符串{minlen = right - left + 1;begin = left;//作為那個字符串的起始位置，因為后面要使用substr}char out = s[left];if (hash2[out] == hash1[out])  count--;hash2[out]--;//判斷完了之后，別忘了將這個字符給題出，因為雖然說left++了，但這個畢竟是另開了一個數組，所以這個數組里面的變化也得跟著原字符串的變化，原字符串++了，那么這個數組只能踢字符了left++;}}if (begin == -1) return "";else return s.substr(begin, minlen);//這個是選取字符串，所以只能在已有的字符串中選取
}
int main()
{string s("ADOBECODEBANC");string t("ABC");string outcome = minWindow(s, t);cout << outcome << endl;return 0;
}

?18.4 總結反思：

處理好一些細節，就可以把一道題做的很好。

19 力扣 704.二分查找

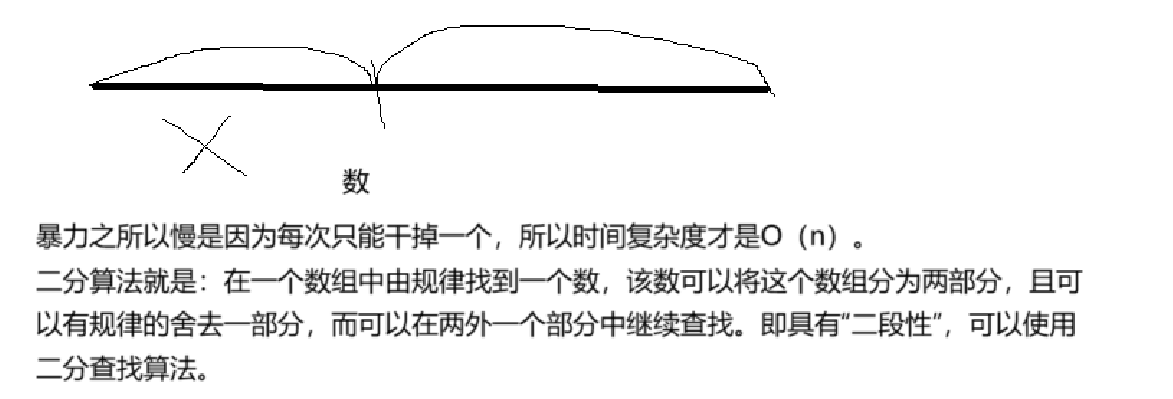
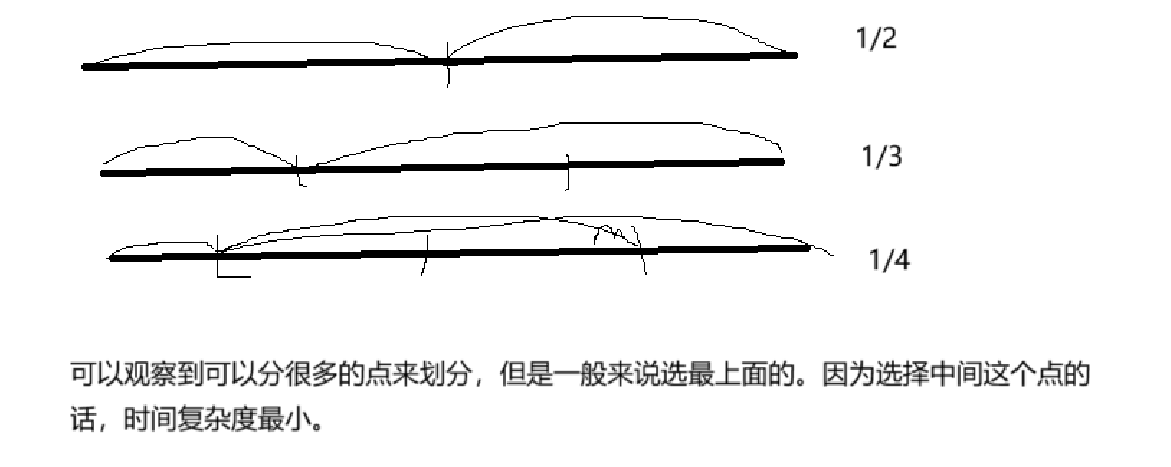
在介紹這道題目之前，先來介紹一下二分算法。

二分算法，可能剛開始使用，會覺得有點難。但是你要是洞悉了二分算法的原理，其實挺簡單的。

且這個算法不管數組有序還是沒序。你只要找到規律之后，都可以使用二分算法的。

19.1?題目解析：

這道題算是我從寫博客以來最簡單的。暴力可以解決，但今天咱們講二分算法。

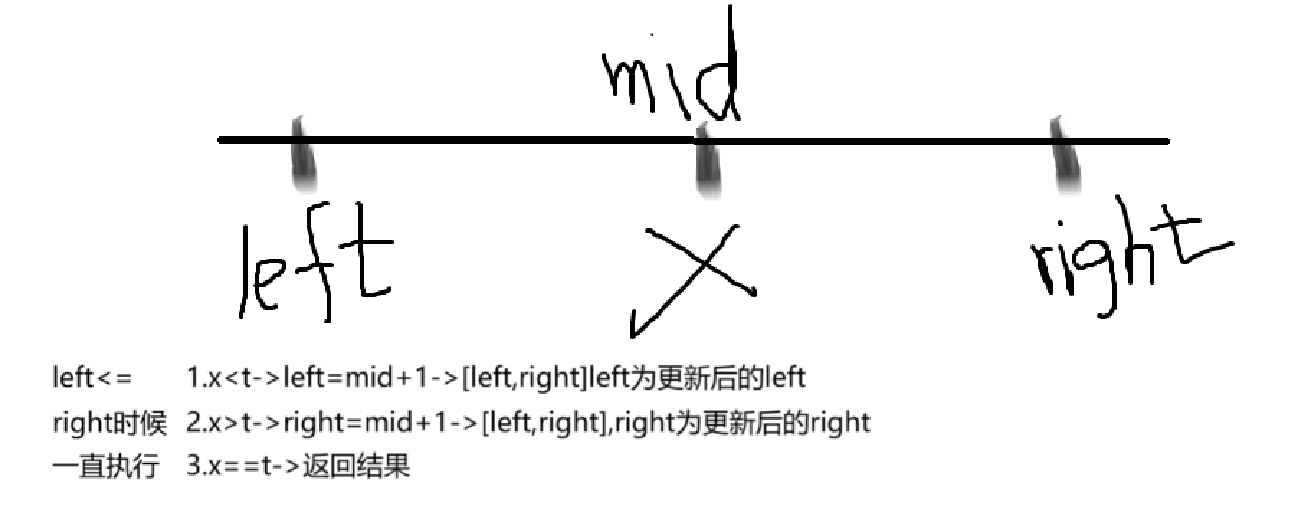
?19.2 算法思路：

?

19.3 代碼演示：

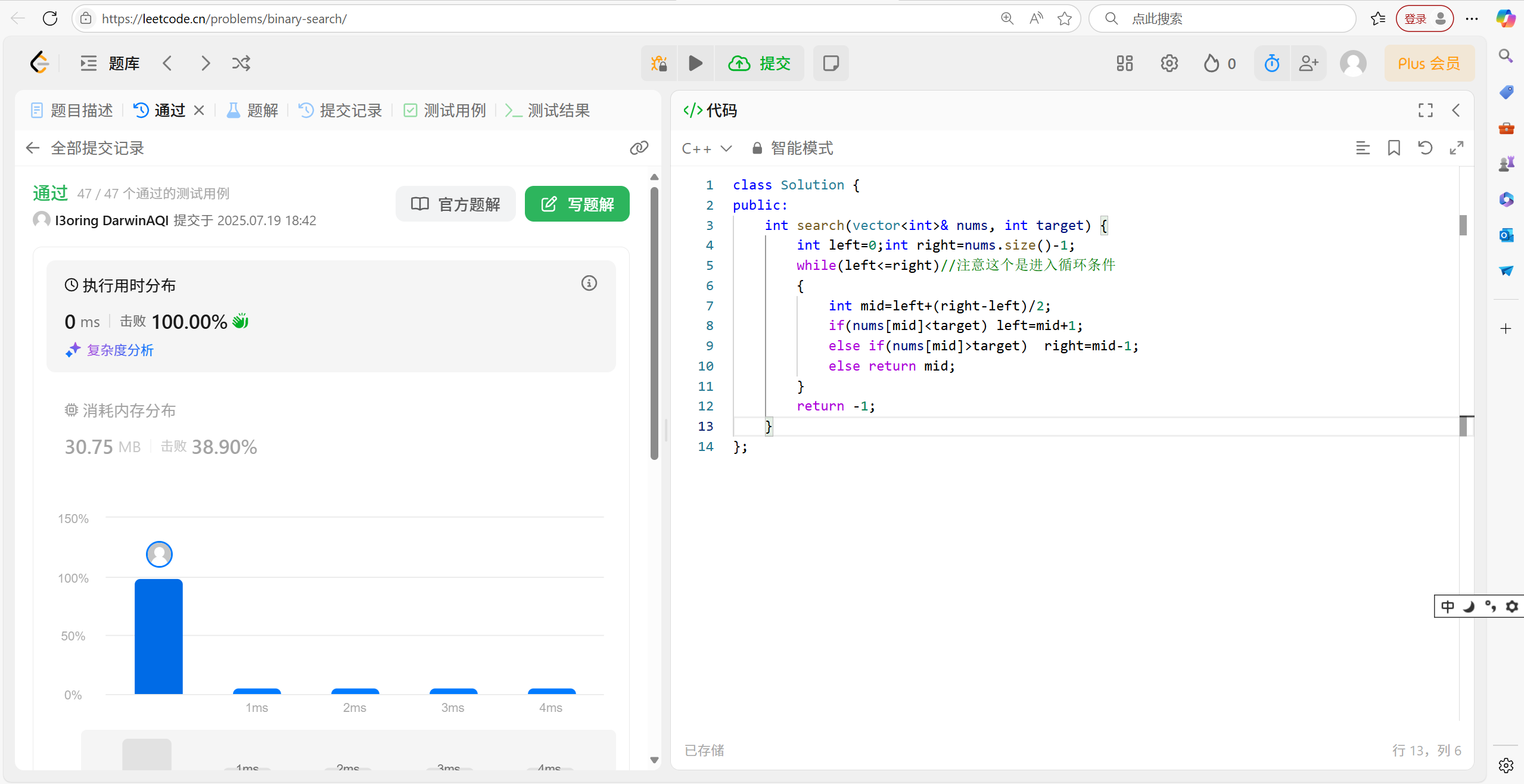
int search(vector<int>& nums, int target) {int left = 0; int right = nums.size() - 1;while (left <= right)//注意這個是進入循環條件{int mid = left + (right - left) / 2;if (nums[mid] < target) left = mid + 1;else if (nums[mid] > target)  right = mid - 1;else return mid;}return -1;
}
int main()
{vector<int> nums = { -1,0,3,5,9,12 };int target = 9;cout << search(nums, target) << endl;return 0;
}

這個求中間點一般是用到(right-left)/2+left。因為如果使用(left+right)/2，left+right會有溢出的風險。

19.4 總結反思：

這只是二分算法的一道開胃小菜。后面還有更大的禮物呢。?

?

?

?

?