螺旋矩陣題型總結。我刷了幾道螺旋矩陣相關的題目，這里我們介紹一下一些常見的解法。

螺旋矩陣

方形矩陣

當我們遇到n*n的方形矩陣時，可以用一種特殊的解法來遍歷實現，以下面這道題為例：

59. 螺旋矩陣 II

我們可以定義幾個變量用來控制遍歷的行為：

• startX：每次循環的起點的行數

• startY：每次循環的起點的列數

• offset：每循環一圈，用偏移量表現

vector<vector<int>> generateMatrix(int n) {vector<vector<int>> ans(n,vector<int>(n,0));int offset = 1 , startX = 0 , startY = 0;int val = 1;int i,j;for(int k=0;k<n/2;k++){     //循環次數就是圈數for(j=startY;j<n-offset;j++)    //左上->右上（從此以下都是左閉右開）ans[startX][j] = val++;for(i=startX;i<n-offset;i++)    //右上->右下ans[i][j] = val++;for(;j>startY;j--)              //右下->左下    ans[i][j] = val++;for(;i>startX;i--)              //左下->右上ans[i][j] = val++;startX++;startY++;offset++;   //實際上更新offset就是在更新每次循環的邊界（縮小）}if (n&1){   //如果矩陣的邊長為奇數，最中間的值會沒法遍歷到ans[offset-1][offset-1] = val;}return ans;}
};

同時還可以將方形矩陣視作一種特殊的矩形矩陣，以下對矩形矩陣的所有解法對方形都適用。

矩形矩陣

有時候我們會發現矩陣是矩形的，或者只有一層，這個時候就需要用幾個通用的方法，來實現。例題：

LCR 146. 螺旋遍歷二維數組

54. 螺旋矩陣

2326. 螺旋矩陣 IV

模擬路徑法

我們先分析我們的轉向條件：（1）當前進的方向上碰到了邊界（2）當前進的方向上是已經走過的路徑

第一個條件比較好解決，第二條件我們需要維護一個和數組相同大小的矩陣，走過的路線我們設置為true，沒走過的設置為false.

由于我們的轉向動作是有序的，是順時針，所以我們可以使用一個數組來存儲我們的方向。當到達轉向條件時，設置成下一個轉向動作。

vector<int> spiralArray(vector<vector<int>>& array) {if(array.empty()||array[0].empty()) //判斷數組是否為空，注意先后順序，array[0]在array為空時是不能訪問的return {};int row = array.size();int col = array[0].size();int total = row*col;vector<vector<bool>> use(row,vector<bool>(col,0));  //路徑表vector<int> ans(total,0);vector<vector<int>> direction{{0,1},{1,0},{0,-1},{-1,0}};   //方向表（順時針）int directionIdx = 0;   //方向表索引int i=0,j=0;for(int k=0;k<total;k++){ans[k] = array[i][j];use[i][j] = true;int ni = i + direction[directionIdx][0];    //預更新iint nj = j + direction[directionIdx][1];    //預更新jif(ni<0||ni>=row||nj<0||nj>=col||use[ni][nj]==true){    //根據預更新狀態判斷轉向條件directionIdx = (directionIdx+1)%4;  //轉向則把方向索引設置到下一位}//實際更新i = i + direction[directionIdx][0];j = j + direction[directionIdx][1];}return ans;}

層級遍歷法（邊界收縮）

這個和剛剛用來解決方形矩陣的方法是相同的，只不過更新方式和更新條件要更加復雜。

一開始先設定好邊界，當移動到邊界的時候就轉向，然后收縮邊界。這樣的好處在于我們不用再特意維護一個數組來判斷路徑是否被走過 了。因為走過的路徑被我們收縮了，所以就不用在考慮。只需要在邊界做檢測就好了。

vector<vector<int>> spiralMatrix(int m, int n, ListNode* head) {vector<vector<int>> ans(m,vector<int>(n,-1));int top = 0;    int bottom = m-1;   //-1是因為索引和實際位置的差值int left = 0;int right = n-1;while(left<=right&&top<=bottom){    //如果相等就說明，邊界收縮了，遍歷結束了for(int i=left;i<=right;i++)    ans[top][i] = val;top++;                          //左上->右上 top邊界收縮for(int i=top;i<=bottom;i++)ans[i][right] = val;right--;                        //右上->右下 right邊界收縮for(int i=right;i>=left;i--)ans[bottom][i] = val;bottom--;                       //右下->左下 bottom邊界收縮for(int i=bottom;i>=top;i--)ans[i][left] = val;left++;                         //左下->右上 left邊界收縮}return ans;}

螺旋生成矩陣

這個算是一個小特例，大多數題目是給你一個矩陣讓你去螺旋遍歷，但是有的題目需要你自己螺旋生成一個矩陣。我們看到下面的例題：

885. 螺旋矩陣 III

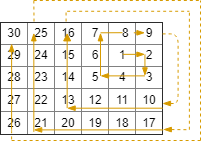
這道題需要我們形成一個螺旋的路徑，然后返回矩形內的位置的坐標。難點在于這個螺旋路徑的生成，因為轉向的條件和每次前進的步長綜合考慮起來條件會非常的復雜。下面的話給出兩種方法。

邊界擴展法

和我們之前所做的邊界收縮相反，我們先界定好邊界，然后每次轉向時寬展這個方向上的邊界。通過這種方式來動態的生成一個螺旋的路徑

const int DIR[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {vector<vector<int>> ans;int total = rows*cols;int num = 1;int i = rStart,j = cStart;  //令i,j記錄路徑的實時位置int left = cStart - 1,right = cStart + 1,top = rStart - 1,bottom = rStart + 1;  //確定邊界int dir=0;  //記錄方向while(num <= total){if(i>=0&&i<rows&&j>=0&&j<cols){ //當路徑到達矩陣內部時，記錄當前位置ans.push_back({i,j});num++;}if(dir==0&&j==right){   //如果向右移動觸碰右邊界dir+=1;             //則轉向right++;            //并拓展右邊界}else if(dir==1&&i==bottom){    //如果向下移動觸碰下邊界dir+=1;                     //則轉向bottom++;                   //并拓展下邊界}else if(dir==2&&j==left){      //...dir+=1;left--;}else if(dir==3&&i==top){       //...dir=0;top--;}i += DIR[dir][0];       //根據方向來更新位置j += DIR[dir][1];}return ans;}

規律法

我們可以觀察螺線路徑的一個顯著規律：每轉向兩次會更新一次前進的步長

const int DIR[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {int num=0;int dir=0;int run=2;  //步長計數器vector<vector<int>> ans;
?while(num < R * C){for(int i = 0; i < run / 2; i ++){ ? //遍歷步長，每轉兩下就會增加一步if(r0 >= 0 && r0 < R && c0 >= 0 && c0 < C)ans.push_back({r0, c0}), ++ num;r0 += DIR[dir][0];c0 += DIR[dir][1];}pos = (pos + 1) % 4;    //每遍歷一次步長，就轉向run++;      //利用取整的性質，每轉向兩次才會增加一次步長}return ans;}

總結

螺旋矩陣的關鍵在于邊界的檢測和變換，還有轉向條件的判斷。比較簡單。