
出品|OKG Research
作者|Hedy Bi
上周末,歐科云鏈研究院接受FT中文的邀請,作為圓桌嘉賓參與了由FT中文網與上海交通大學上海高級金融學院聯合主辦的金融大師課。在圓桌環節,筆者與各位教授和金融行業科技創新前沿實踐者深入探討了科技、金融與人類的復雜關系,以及它們對未來的深遠影響。特別值得一提的是,上海交通大學上海高級金融學院兼聘教授劉曉春教授在此次大師課上梳理了幾十年來金融業的發展脈絡。他提出的一個觀點引我深思:金融業實際上承擔了整個社會的風險成本,而這往往被誤解為金融本身的問題。

圖為FT中文聯合上海交通大學上海金融高級學院的SAIF金融MBA教授公開課暨大咖對話活動現場照片
劉教授的洞見不禁讓我聯想到Web3領域近年來所面臨的褒貶不一的評價。正如劉教授所言,新興科技往往會被不法分子迅速利用,但這并非科技本身的缺陷,反而應該成為行業從業者加速創新應用的動力。放眼2024年,Web3行業正迎來新的發展機遇:美國和香港地區正逐步將比特幣和以太坊納入主流金融體系,吸引了大量投資者的目光。以美國市場為例,通過現貨ETF渠道流入的資金總額已達147億美元。雖然這個數字乍看頗為可觀,但并未引起市場更大的波瀾。除了整個市場的底層邏輯在轉變外,筆者就本文想談談我們現在身處何處以及正走向何方。
原生性創新停滯,未來從金融科技走向科技金融
從金融科技(Fintech)到科技金融(Techfin)已經是互聯網和金融行業正在進行中的發展趨勢了。而在Web3也有相似的趨勢,我們觀察到,屬于原生性創新階段已經告一段落,例如DeFi、NFT、代幣化等方式都屬于用科技加持金融或者資產的流動。自2018年Uniswap創立以來,DeFi DApp鏈上資產的總鎖倉量從最初的42萬美元增長到2021年的最高峰1790億美元,短短3年期間增長了約42萬倍。在此期間,許多人通過Web3的機遇致富,因此Web3被年輕一代譽為經濟下行周期中的少有致富機會和增長行業。
在本周召開的高盛Digital Assets Conference中,Animoca Brands聯合創始人兼執行主席Yat Siu提到,加密世界與現實世界的結構相似且具有先進性。目前,DeFi的規模已經是全球最大央行資產規模之一。根據具體數據,這個資產規模已經可以在全球近200個國家中排名前30位。

然而,自今年BTC現貨ETF通道開啟后,投資者的目光紛紛轉向BTC等主流交易品種,Web3的原生創新似乎進入了一個暫時的停滯期。從利用科技工具提供金融效率(金融科技)到從科技公司反哺金融為用戶提供金融便利,歐科云鏈集團也是從最開始圍繞數字金融提供科技工具到夯實鏈上數據的各種場景下的商用,再到現如今,利用我們超過180個國家的用戶基礎促進Web3科技與金融不斷融合和發展。
未來,我們將會看到科技公司利用其龐大的用戶流量基礎和數據優勢快速進入Web3,尤其是應用層面。除了和傳統金融的跨界合作產品誕生外,我們還可以期待的是類似于ChatGPT這種能夠迅速聚集百萬用戶的超級應用,這些應用不僅會給Web3打開新局面,更是會為科技金融帶來新的工具。
無論近日Meta計劃將更多生成式AI技術集成到VR、AR和混合現實游戲中,以振興其元宇宙戰略的新聞還是微軟早在22年收購暴雪游戲,在23年與Aptos Labs合作開發新的區塊鏈AI工具還是歐科云鏈集團已經在用AI優化和提高底層平臺的效率等等,這些都是勢不可擋的未來發展趨勢。
盡管元宇宙的發展曾遇空城,但未來,在元宇宙領域中的游戲和社交這個分支將會隨著硬件的完備和AI的催化,會有可能爆出超級應用。此外,我們還可以觀察到從Web3原生出的一些科技巨頭也正在從Web3錢包、交易平臺等向更廣大用戶拓展。
東西方方向分化,科技巨頭選擇各不同
我們深入了東西方科技巨頭在Web3領域探索較多的幾家公司近1-2年發展情況,總結下來,可以發現在戰略重點、技術實現、市場定位方面均有不同:
在戰略重點上,東方的科技公司更加注重將區塊鏈技術應用于企業級服務和產業數字化,例如供應鏈金融、數據共享和開源社區發展,例如百度、騰訊提供企業級技術解決方案;西方則在近幾年將目光轉向了更加廣泛地探索區塊鏈和Web3技術在消費市場和創新領域的應用,包含VR、NFT和游戲等領域進行探索,旨在為消費者創造新的數字市場和應用體驗,例如蘋果和Meta在硬件上發力,TikTok和谷歌則支持NFT在已有的用戶群體中的一些應用,Google母公司Alphabet在24年初還繼續對Web3領域進行投資等等。
在技術實現上,東方公司傾向于自有人員直接開發;而西方則傾向于開放合作和生態系統建設,例如Microsoft與Animoca Brands的合作、與Aptos Labs的合作,來快速推動技術創新和市場采用。
在市場定位上,東方公司傾向于本土市場的深耕,而西方則傾向于利用Web3的全球性去進行推廣,例如Google Cloud在Tezos區塊鏈的驗證者角色,顯示了其全球化戰略和影響力。
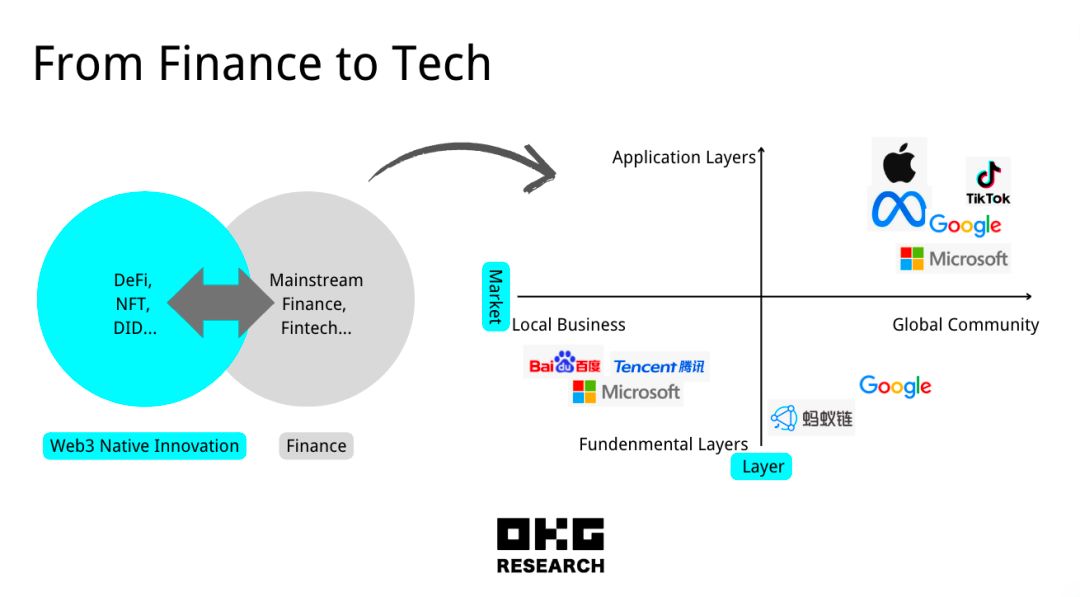
本圖僅根據有限的公開信息進行梳理,信息截止到2024年7月1日。
基于Web3社區的無國界和全球性特點,我們可以看到一些科技公司迅速融入到了Web3生態系統中。因此,在應用層面上,直接跨越本地市場進行擴展,Web3社區的特性使得全球業務的開展變得更加容易。歐科云鏈作為Web3科技的領航者,也切身感受到Web3市場的全球化特性。目前,根據公開資料分析,西方互聯網巨頭在基礎建設這個環節完成后目前已轉移到應用層,而東方的互聯網巨頭則還未曾看到這一明顯趨勢。
雖然,我們觀察到Web3已走入一個十字路口:原生性創新處于停滯狀態,東西方科技巨頭和金融巨頭正在不斷地進入Web3領域。隨著金融和科技兩大巨頭不斷與之融合,這兩股力量如同雙手托舉著Web3產業走向蓬勃發展。
本文僅根據公開信息代表個人觀點,不構成對任何潛在投資目標的推薦或意見,亦不得視為投資建議。



)



)








)



)