1、二分查找法 Binary Search

找一個數，有序的情況下，直接遍歷找，時間復雜度為O(n)，用二分法，一半一半的砍著找，則時間復雜度為O(log n)，更優

核心：左、中、右三個指針的移動

2、leetcode704：二分查找

注意下面對中間指針的求法，不寫 (l + r ) / 2，寫成 l + (r - l) / 2，二者通分后值一樣，但l + r可能超出int的最大值，后者這種寫法則可規避這個問題。且 除二可以改為位運算 >> 1，其快于除法運算，注意右移的運算優先級很低，要加括號（a + b >> c 會首先執行加法 a + b，然后將結果右移 c 位）

public class P704 {public static int binarySearch(int[] array, int value) {if (array == null || array.length == 0) {return 0;}int left = 0;int right = array.length - 1;int mid;while (left <= right) {mid = left + (right - left) / 2;if (array[mid] > value) {// 右邊半截不要了right = mid - 1;} else if (array[mid] < value) {// 左邊半截不要了left = mid + 1;} else {return mid;}}return -1;}
}

測試：

public class P704 {public static void main(String[] args) {int[] num = {-1, 0, 3, 5, 9, 12};System.out.println(binarySearch(num, 9));System.out.println(binarySearch(num, 10));}}

3、leetcode35：搜索插入位置

第一個想法是：先普通的二分查找value，返回-1后，說明不存在，那就再遍歷這個數組，用雙指針，當p1的值 < value && p2的值 > value時，return p1 + 1，但這樣應該是復雜了

換個想法，只需調整下普通的二分查找：這題要求找值target，有就返回下標索引，無就返回插入后的下標索引，因此，這題要找第一個大于等于target的值的下標索引，如果有等于target的，那返回其下標，如果不存在，那就要插入到第一個比target大的值的位置，第一個大的值的下標則往后移動一位。

public class P35 {public static int searchOrInsert(int[] array, int target) {if (array == null || array.length == 0) {return 0;}int left = 0;int right = array.length - 1;int ans = array.length;while (left <= right) {int mid = ((right - left) >> 1) + left;if (target == array[mid]) {// 如果有，直接返回return mid;} else if (target < array[mid]) {// 如果mid大于target，存一下mid的值// 此時mid是大于target的值，但不一定是第一個大于target的值ans = mid;right = mid - 1;} else {// 左指針右移，說明target很大，極限時，插入到末尾，此時return array.length即末尾left = mid + 1;}}return ans;}
}

4、leetcode162：尋找峰值

一頭一尾是負無窮，所以，即使是1，2，3，4這個輸入，也有峰值：4

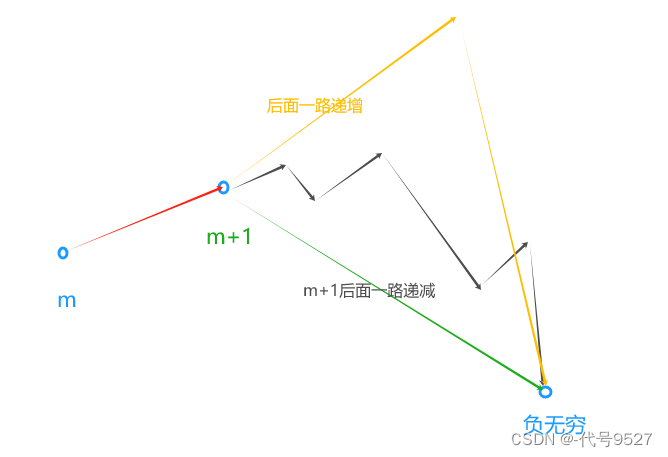
m+1 > m時，m+1到right之間一定有一個峰值，不論m的左側是單增、單減、波浪起伏。此時可把左指針移動到m+1的位置，減少搜索范圍。

public class P162 {public static int getPeak(int[] array) {if (null == array || array.length == 0){return -1;}int left = 0;int right = array.length - 1;// 這兒不能允許left==right,否則當left=right=末尾元素時，mid也就是末尾元素，mid+1就越界了while (left < right) {int mid = left + ((right - left) >> 1);//說明mid和mid+1兩個點，從左到右是下降的，mid自身或者mid的左邊可能有峰值if (array[mid] > array[mid + 1]) {right = mid;} else {// 一定有個峰值出現在mid+1到right之間left = mid + 1;}}return left;}
}

5、leetcode74：搜索二維矩陣

如題，這樣特點的矩陣，本身就是遞增的，如圖中的1、3、5、7、10、11、16……

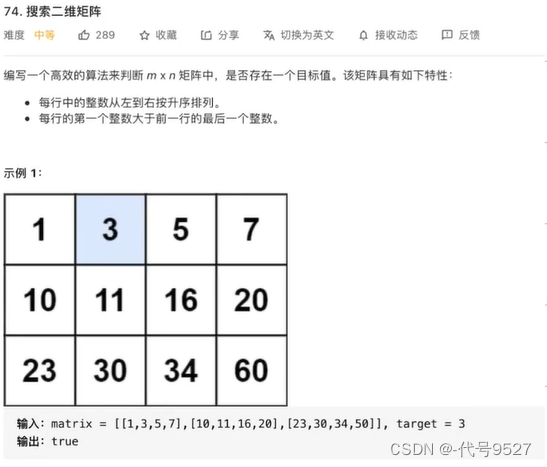
在有序的集合里找一個數字，可以二分查找。但現在雖然有序，卻不是集合，是一個二維數組，那把矩陣拍平后就是一個簡單的二分查找了。把這個矩陣（二維數組）拍平有兩種思路：

• 直接遍歷二維數組，把每個元素裝入一位數組，但這樣得兩層for，時間復雜度太高
• 思想上拍平，將二維數組的索引，和一維數組建立聯系

考慮將二維數組的索引（x，y）轉為一維的索引i，。關于二維索引和一維索引的相互轉換，發現：

將二維索引(x，y)和一維索引 i 標出來，得出：一維索引的坐標 i = x * 列總數 + y

如上面總列數為4，(0,0)對應的一維坐標正好是 0 * 4 + 0 = 0

如此，不用遍歷二維數組，就可將矩陣的每個數都對應一個一維坐標。二分法時，起始左指針 = 0， 右指針 = 行數 × 列數 - 1（即總元素數），計算出mid后，無法根據mid索引在二維數組中取值，需要將一維坐標再倒回去，x = i / 列總數 ，y = i % 總列數

public class P74 {public boolean matrixSearch(int[][] matrix, int target) {if (null == matrix || matrix.length == 0) {return false;}// 行數int row = matrix.length;// 列數int col = matrix[0].length;// 左右指針起始位置int left = 0;int right = row * col - 1;while (left <= right) {int mid = left + (right - left) / 2;// 無法根據一維的mid索引在二維數組中取值，需要將一維坐標再倒回去// x = i / 列總數 ，y = i % 總列數int element = matrix[mid / col][mid % col];if (target == element) {return true;} else if (target < element) {right = mid - 1;} else {left = mid + 1;}}return false;}
}