本節博客詳述“二分查找”并且以例子來進行討論,有需要借鑒即可。
目錄
- 1.二分查找
- 1.1使用前提
- 1.2模板
- 2.題目
- 3.題解代碼示例
- 4.二分查找的一般模板
- 5.總結
1.二分查找
1.1使用前提
使用的條件:數組具有“二段性”,二段性指的是數組可以根據某一規律分為兩組,且在干掉一半之后仍可以對另一半進行復用相同的規律。
1.2模板
二分查找的代碼具有高度統一性,因而可以套用模板,但這并不意味著自己不需要用腦子無腦套模板。
一般二分查找模板、查找左邊界二分模板、查找右邊界二分模板。
下面是通過一道具體的題目來介紹二分查找算法的由來。
2.題目
題目鏈接:LINK

首先肯定是暴力解法,挨個遍歷就行了,找到了返回對應的下標,找不到返回-1
但是這個暴力解法有點慢,慢就慢在一次只能干掉一個數字。
有序數組滿足“二段性”,這里的“二段性”就是以某個數字作比較,可以將數組分為比這個數字大的一組和小的一組,因而可以利用有序的特點直接上二分查找算法。
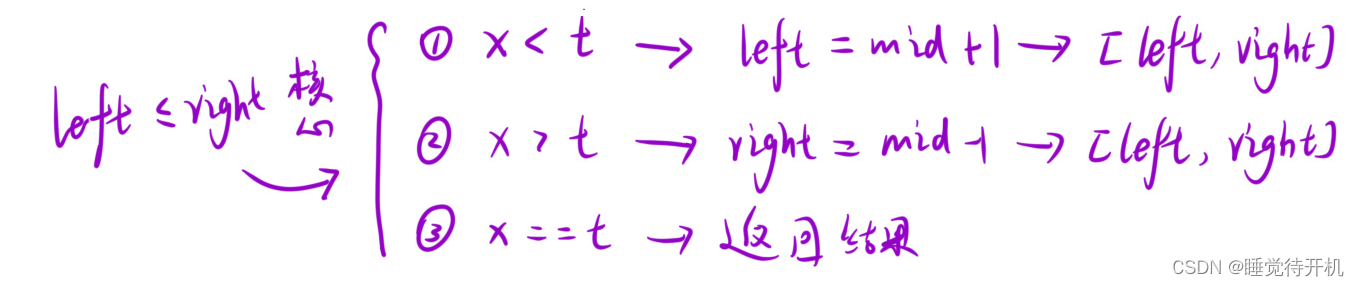
思考:結束條件是什么?
答:left <= right,這個等于一定要注意,因為一個數字也要判斷一下。
不然會出下以下“悲劇”:
思考:為什么一定得二分,而不是三分、四分…N分?
答:這里推一篇文章,有興趣可以看一下:LINK
二分查找復雜度
答:logN
3.題解代碼示例
class Solution {
public:int search(vector<int>& nums, int target) {//一般情況for(int left = 0,right = nums.size() - 1,mid; left <= right;){//mid = (left + right) / 2;mid = left + (right - left) / 2;//優化,防止兩數相加溢出問題if(nums[mid] > target)right = mid - 1;else if(nums[mid] < target)left = left + 1;else return mid;}return -1;}
};
4.二分查找的一般模板
while(left < right)
{
int mid = left + (right - left) / 2;
if(...)
//
else if(...)
//
else
return ...
}
5.總結
我感覺二分查找大部分人是比較熟悉的,這里需要注意兩個點,為什么是二分?二分查找的使用前提一定是有序嗎?
題目太簡單,不多說。
EOF
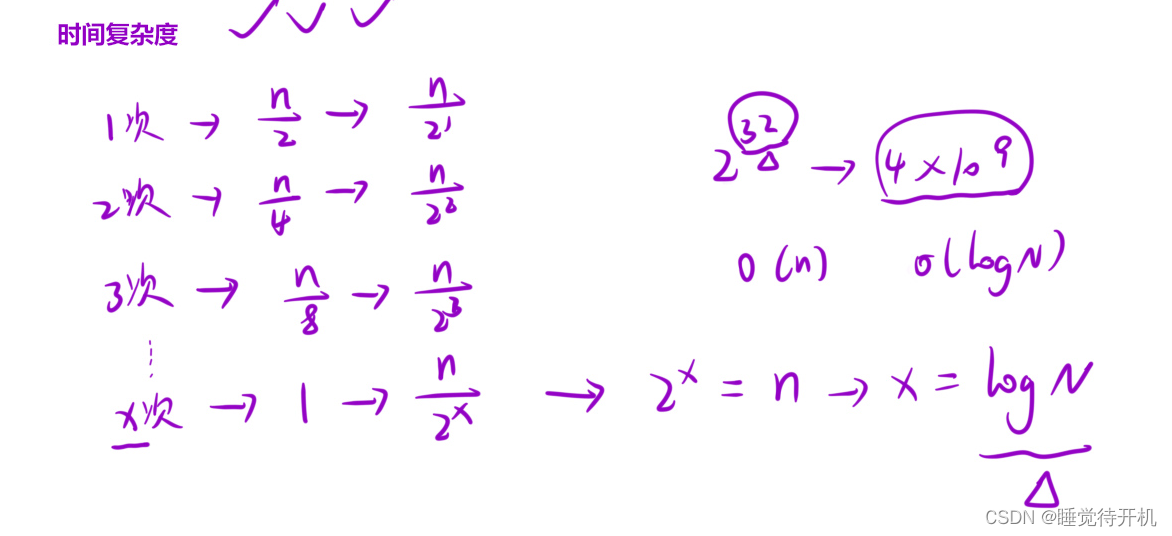
,超實用!)
)
接口自動化測試requests)


![[藍橋杯]真題講解:抓娃娃(思維+二分)](http://pic.xiahunao.cn/[藍橋杯]真題講解:抓娃娃(思維+二分))

)










)
