引言

前序學習文章中，已經探究了電荷超平面的距離計算方法，相關文章為點與超平面的距離。
在這片文章中，我們了解到計算距離的公式：
$$F=\underset{i=\mathrm{1...}m}{\min }{y}_i(w?x_i+b)$$

計算點與超平面的距離

對此，可以書寫代碼進行計算：

# 引入numpy模塊
import numpy as np# 定義example_functional_margin()函數
def example_functional_margin(w,b,x,y):# 先對w和x兩個參數執行點擊運算，然后添加偏置量b后與y相乘result = y*(np.dot(w,x)+b)return result# 定義functional_margin()函數
def functional_margin_array(w,b,X,y):# 直接調用example_functional_margin()函數，按照枚舉函數的順序，逐個計算return np.array([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])# 定義functional_margin()函數
def functional_margin(w,b,X,y):# 直接調用example_functional_margin()函數，按照枚舉函數的順序，逐個計算return np.min([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])x=np.array([[1,1],[2,2]])
y=1b_1=5
w_1=np.array([2,1])w_2=w_1*10
b_2=b_1*10# 所有結果均輸出
print(functional_margin_array(w_1,b_1,x,y))
print(functional_margin_array(w_2,b_2,x,y))
# 最小結果輸出
print(functional_margin(w_1,b_1,x,y))
print(functional_margin(w_2,b_2,x,y))

代碼運行效果為：

在上述代碼中，我們會有一個發現：在向量x不改變的前提下，如果等比率調整權重向量w和偏置量b，獲得的距離F也會等比率變化。而對于超平面計算公式$$w?x+b=0$$
w和x無論擴大多少倍，公式依然成立。
因此，必須進一步修正點與超平面的計算公式，消除w和b按比率變化的影響。

點與超平面距離公式修正

在先前的學習進程中，通過向量的值和方向我們已經掌握方向向量的計算方法：
$$w=(\frac{w_1}{\Vert w\Vert },\frac{w_2}{\Vert w\Vert })$$由上式可知，方向向量是一個單位向量，一個向量無論放大多少倍，方向向量都不會改變。

因此，合理的點與超平面計算公式應當回歸到將w轉化為單位向量，使得所有計算基準統一，定義此時的距離為幾何距離δ：$$\delta =\underset{i=\mathrm{1...}m}{\min }{y}_i(\frac{w}{\Vert w\Vert }?x+\frac{b}{\Vert w\Vert })$$
δ的計算和F最大的不同在于：將權重向量統一為單位向量。
此時再次計算點與超平面的距離時就不用擔心權重向量w和偏置量b的取值。

# 引入numpy模塊
import numpy as np# 定義example_functional_margin()函數
def example_functional_margin(w,b,x,y):# 先對w和x兩個參數執行點擊運算，然后添加偏置量b后與y相乘result = y*(np.dot(w,x)+b)return result# 定義functional_margin()函數
def functional_margin_array(w,b,X,y):# 直接調用example_functional_margin()函數，按照枚舉函數的順序，逐個計算return np.array([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])# 定義functional_margin()函數
def functional_margin(w,b,X,y):# 直接調用example_functional_margin()函數，按照枚舉函數的順序，逐個計算return np.min([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])x=np.array([[1,1],[2,2]])
y=1b_1=5
w_1=np.array([2,1])w_2=w_1*10
b_2=b_1*10# 所有結果均輸出
print(functional_margin_array(w_1,b_1,x,y))
print(functional_margin_array(w_2,b_2,x,y))
# 最小結果輸出
print(functional_margin(w_1,b_1,x,y))
print(functional_margin(w_2,b_2,x,y))# 將計算基準轉化為權重矩陣的單位向量
def example_functional_margin_unit_ector(w,b,x,y):unit=np.linalg.norm(w)result=y*(np.dot(w/unit,x)+b/unit)return result# 計算基于單位向量的距離
def geometric_margin(w,b,X,y):return np.array([example_functional_margin_unit_ector(w,b,x,y)for i,x in enumerate(X)])# 輸出單位向量基準的距離
print(geometric_margin(w_1,b_1,x,y))
print(geometric_margin(w_2,b_2,x,y))

此時的計算結果為：

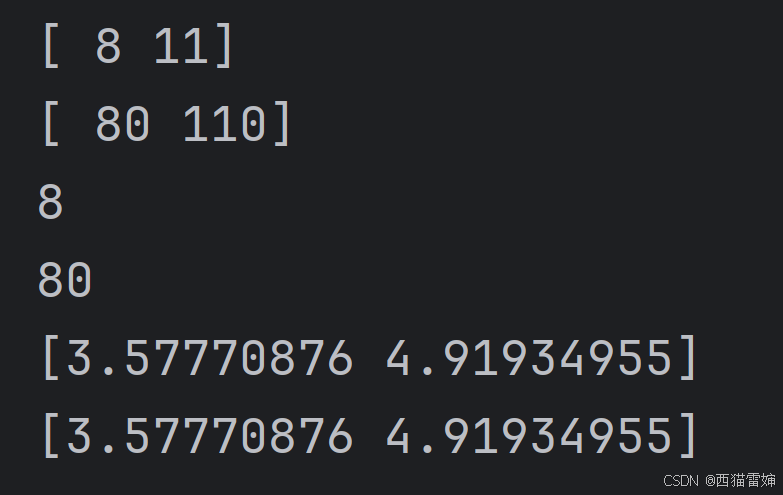
由計算效果可見，此時盡管w放大10倍，但計算獲得的幾何距離值不變。

總結

學習了幾何距離的定義和計算。