????????今天繼續回溯算法的專題，第三篇博客！

93.復原IP地址

輸入：s = "25525511135"
輸出：["255.255.11.135","255.255.111.35"]

????????切割字符串為4段，當進行到第四段的時候對第四段字符串進行判斷，是否可以輸出到result數組中，優化：通過檢查剩余位數來進行剪枝

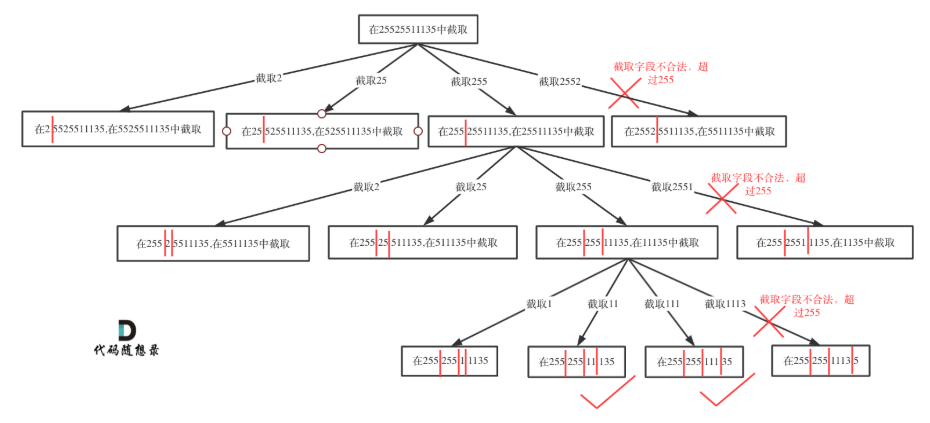
回溯過程

• 遞歸參數

????????startIndex一定是需要的，因為不能重復分割，記錄下一層遞歸分割的起始位置。本題我們還需要一個變量pointNum，記錄添加逗點的數量。（記錄已經是多少段了）

• 遞歸終止條件

????????本題明確要求只會分成4段，所以不能用切割線切到最后作為終止條件，而是分割的段數作為終止條件。pointNum表示逗點數量，pointNum為3說明字符串分成了4段了。然后驗證一下第四段是否合法，如果合法就加入到結果集里

• 單層搜索的邏輯

????????在for (int i = startIndex; i < s.size(); i++)循環中 [startIndex, i] 這個區間就是截取的子串，需要判斷這個子串是否合法。

• 如果合法就在字符串后面加上符號.表示已經分割。
• 如果不合法就結束本層循環，如圖中剪掉的分支：

????????然后就是遞歸和回溯的過程：遞歸調用時，下一層遞歸的startIndex要從i+1開始，同時記錄分割符的數量pointNum 要 +1。回溯的時候，就將剛剛加入的分隔符.?刪掉就可以了，pointNum也要-1。

判斷子串是否合法

主要考慮到如下三點：

• 段位以0為開頭的數字不合法
• 段位里有非正整數字符不合法
• 段位如果大于255了不合法

回溯模版

void backtracking(參數) {if (終止條件) {存放結果;return;}for (選擇：本層集合中元素（樹中節點孩子的數量就是集合的大小）) {處理節點;backtracking(路徑，選擇列表); // 遞歸回溯，撤銷處理結果}
}

代碼實現

class Solution:def restoreIpAddresses(self, s: str) -> List[str]:result = []self.backtracking(s, 0, 0, '', result)return resultdef backtracking(self, s, start_index, point_num, current, result):# start_index: 標注下一層的循環開始位置# point_num: 切割逗點數量# current: 單個字符串保存# result: 結果數組集合存儲if point_num == 3: #分割結束if self.is_valid(s, start_index, len(s) - 1):# 符合左閉右閉, 數組索引方式current += s[start_index: ]# 添加最后一段字符串result.append(current)return for i in range(start_index, len(s)):# range函數左閉右開# 判斷該段字符是否符合, 如果不符合停止該層遞歸if self.is_valid(s, start_index, i): # 理解i的作用片段, 符合要求sub = s[start_index:i+ 1] # 切片左閉右開self.backtracking(s, i + 1, point_num + 1, current + sub + '.', result)# 理解python中的引用復制和復制賦值！else:breakdef is_valid(self, s, start, end):# 左閉右閉if start > end:return Falseif s[start] == '0' and start != end:# 開頭數字為0return Falsenum = 0for i in range(start, end + 1):if not s[i].isdigit():return False # 判斷是否遇到非數字字符num = num * 10 + int(s[i])if num > 255:return Falsereturn True

版本2（了解即可）

class Solution:def restoreIpAddresses(self, s: str) -> List[str]:results = []self.backtracking(s, 0, [], results)return resultsdef backtracking(self, s, index, path, results):if index == len(s) and len(path) == 4:results.append('.'.join(path))returnif len(path) > 4:  # 剪枝returnfor i in range(index, min(index + 3, len(s))):if self.is_valid(s, index, i):sub = s[index:i+1]path.append(sub)self.backtracking(s, i+1, path, results)path.pop()def is_valid(self, s, start, end):if start > end:return Falseif s[start] == '0' and start != end:  # 0開頭的數字不合法return Falsenum = int(s[start:end+1])return 0 <= num <= 255

78.子集

????????簡單題目，屬于組合范疇（普通模版級別），大家可以自己畫一畫樹狀圖

回溯過程

• 遞歸函數參數

????????全局變量數組path為子集收集元素，二維數組result存放子集組合。（也可以放到遞歸函數參數里）遞歸函數參數在上面講到了，需要startIndex。

• 遞歸終止條件

? ? ? ? 所剩集合為空的時候，就是葉子節點。那么什么時候剩余集合為空呢？就是startIndex已經大于數組的長度了，就終止了，因為沒有元素可取了

• 單層搜索邏輯

????????求取子集問題，不需要任何剪枝！因為子集就是要遍歷整棵樹。

class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:result = []path = []self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):result.append(path[:])for i in range(startIndex, len(nums)):path.append(nums[i])self.backtracking(nums, i + 1, path, result)path.pop()

90.子集II

????????整數數組?nums?，其中可能包含重復元素，這個是困難的，所以要去重

????????之前我們也做過一道去重的題目，更具體的說，這個就是“樹枝去重”和“樹層去重”的區別，毫無疑問，我們這道題仍然是樹層去重，即樹枝上存在相同元素是允許的，而書層上出現相同元素是不被允許的

? ? ? ? 整體思路如下：是和之前“去重”思路完全一樣的題目

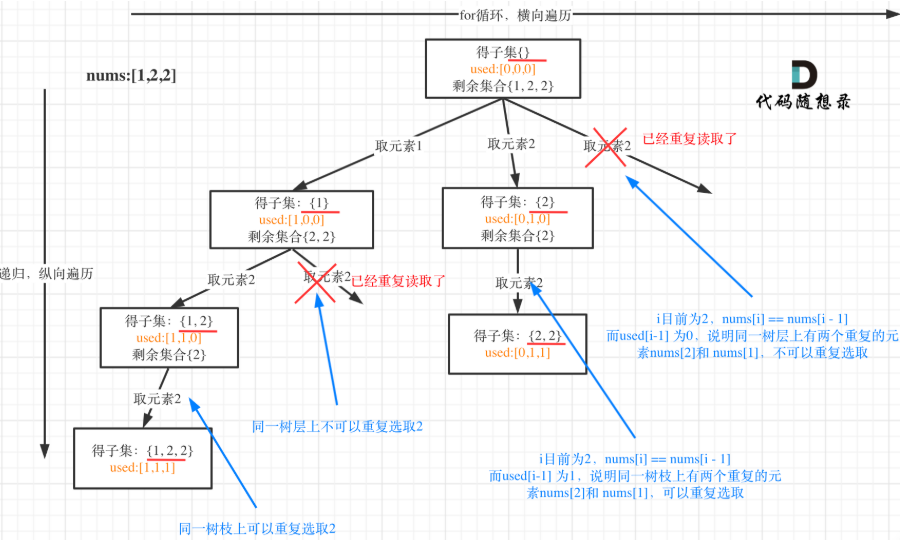
代碼實現（增加去重）

class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:result = []path = []nums.sort()# 注意排序,這樣相同的數字才可以放在一起,方便后續處理self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):result.append(path[:])for i in range(startIndex, len(nums)):if i > startIndex and nums[i] == nums[i - 1]: # 第一個遇到不要處理continuepath.append(nums[i])self.backtracking(nums, i + 1, path, result)path.pop()

代碼實現（利用used數組）

class Solution:def subsetsWithDup(self, nums):result = []path = []used = [False] * len(nums)nums.sort()  # 去重需要排序self.backtracking(nums, 0, used, path, result)return resultdef backtracking(self, nums, startIndex, used, path, result):result.append(path[:])  # 收集子集for i in range(startIndex, len(nums)):# used[i - 1] == True，說明同一樹枝 nums[i - 1] 使用過# used[i - 1] == False，說明同一樹層 nums[i - 1] 使用過# 而我們要對同一樹層使用過的元素進行跳過if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:continuepath.append(nums[i])used[i] = Trueself.backtracking(nums, i + 1, used, path, result)used[i] = Falsepath.pop()