題目

在例10.1中，把數據模型修正為：

其中是WGN，如果，那么方差，如果，那么方差。求PDF 。把它與經典情況PDF 進行比較，在經典的情況下A是確定性的，是WGN，它的方差為：a. ; b.

解答：

經典情況下，是WGN，也就是：

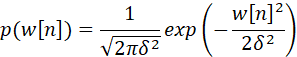
而經典情況下，A是確定的，因此可以轉換為：

又因為是WGN，屬于獨立同分布，因此：

因此，經典條件下，表示無條件PDF，可以看成是未知參數的函數，用于參數估計時，也稱之為似然函數。

---

而在貝葉斯情況下，A也是隨機變量，且根據題目設定，的方差與A的取值有關，因此兩者就不獨立了，進一步可以表示為：

因此：

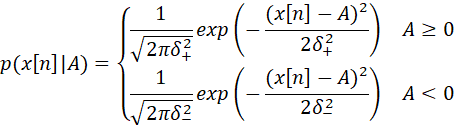
由于在確定條件A下，之間相互獨立，因此，聯合概率密度也可以直接相乘，進一步可以表示為：

對比可以發現，當時：

但時：

需要進一步注意的是，盡管當時，在函數形式上兩者相等，即：，但兩者的物理意義是不同的。具體的描述可以參考書（10.7）公式后的描述。

是關于A的函數，即A是個確定性參數，但A有不同取值。是在不同A的取值，這一組取值的概率大小，此時屬于無條件PDF。取最大值對應的A，就是極大似然估計下的；

是一種條件概率，即隨機變量為A時，的概率大小，此時屬于條件PDF。但由于此時隨機變量取A的概率還不知道。因此，要在A在不同取值概率的情況下，整體也是關于隨機變量A的函數。求該整體最大值對應的A，對應就是MAP估計下的。