1.簡介

????????1.二分查找的思路簡單易懂，較難的是如何處理查找過程中的邊界條件，當較長時間沒寫二分查找的時候就容易忘記如何處理邊界條件。

? ? ? ? 2.只有多寫代碼，多做筆記就不易忘記邊界條件

2.算法思路

? ? ? ? 正常查找都是從頭到尾查找一個數字是否在數組中

? ? ? ? 二分查找適用于已經有序的數組，利用有序的這個性質，定義兩個指針，left指向頭，right指向尾，定義一個mid為頭尾指針的平均值。

首先選擇mid位置的數字和目標值比較

中間值與target相等直接返回這個數字的下標即可

如果不相等

????????如果mid位置的數字數字大于目標值，則mid位置的數字向右的所有數字都大于target，全部排除,讓mid-1變為新的尾部

????????如果mid位置的數字數字小于目標值，則mid位置的數字向左的所有數字都小于target，全部排除，讓mid+1成為新的頭部

最后left>right的話說明該數組中沒有target這個數字

? ? 示例

????????給定一個?n?個元素有序的（升序）整型數組?nums?和一個目標值?target??，寫一個函數搜索?nums?中的?target，如果目標值存在返回下標，否則返回?-1。

? ? ? ?

????????示例1

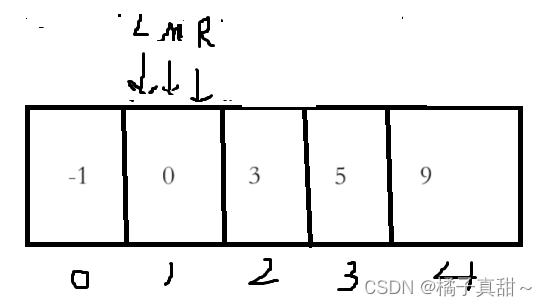
? ? ? ? ?nums=[-1,0,3,5,9,] target=9? ? ? ? 輸出4,因為數組中有9，且其下標尾4

下面給出查找的過程

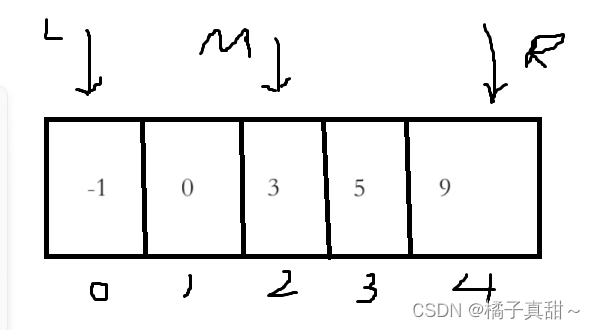
mid處為3，3<9,所以讓mid+1成為新的頭部(left=mid+ 1)

如下圖

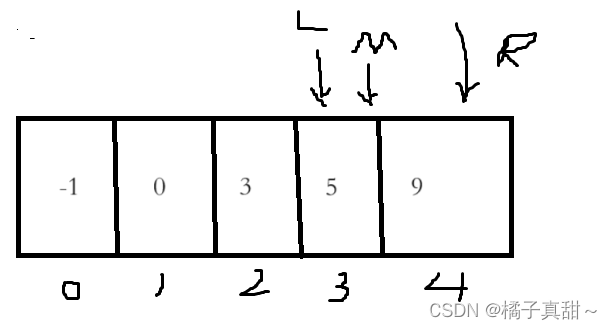
5<9,再次縮小左邊界

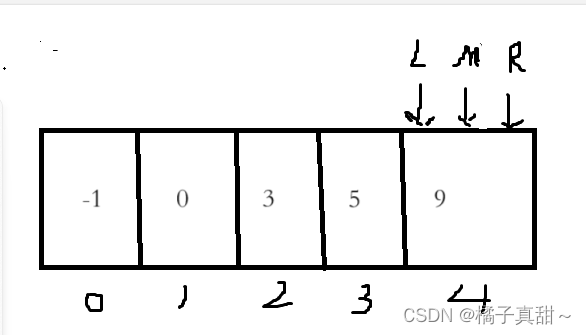
找到了，返回mid下標4

? ? ? ? 示例2? ? ? ?

????????nums=[-1,0,3,5,9,] target=2? ? ? ? 輸出-1,因為數組中沒有2

同理給出過程

3>2,縮小右邊界 right=mid-1

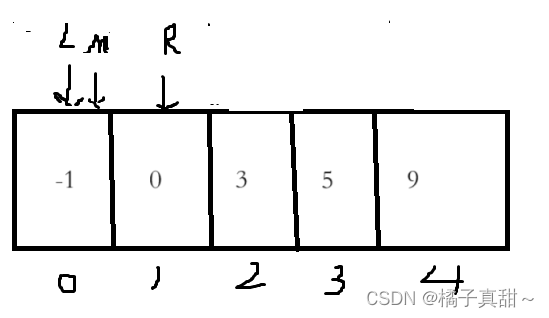
此時，新的mid為(0+1)/2=0

-1<2,讓left=mid+1

此時0<2,讓left=mid+1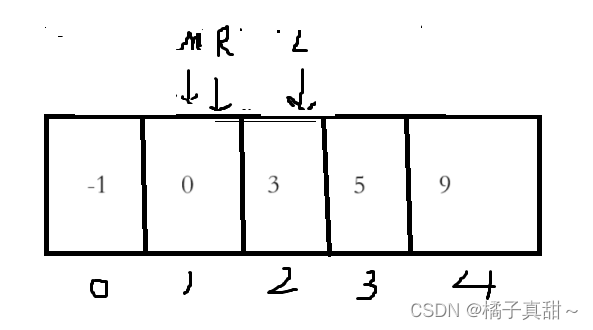

left>right.說明整個數組中沒有目標值，返回-1

3.實現代碼

代碼如下

int BinarySearch(vector<int>& arr, int target)
{if (arr.size() < 1)return -1;int left = 0, right =arr.size() - 1;while (left <= right){int mid = left + ((right - left) >> 1);if (arr[mid] > target)right = mid - 1;else if (arr[mid] < target)left = mid + 1;elsereturn mid;}//沒找到return -1;
}

4.二分查找的特點

時間復雜度:O(logN)

空間復雜度:O(1)

適用于查找有序的數組

5.簡單測試

測試代碼

int BinarySearch(vector<int>& arr, int target)
{if (arr.size() < 1)return -1;int left = 0, right =arr.size() - 1;while (left <= right){int mid = left + ((right - left) >> 1);if (arr[mid] > target)right = mid - 1;else if (arr[mid] < target)left = mid + 1;elsereturn mid;}//沒找到return -1;
}int main()
{vector<int> arr = { -1,0,3,5,9 };cout << BinarySearch(arr, 9) << endl;cout << BinarySearch(arr, 2) << endl;return 0;
}

測試結果

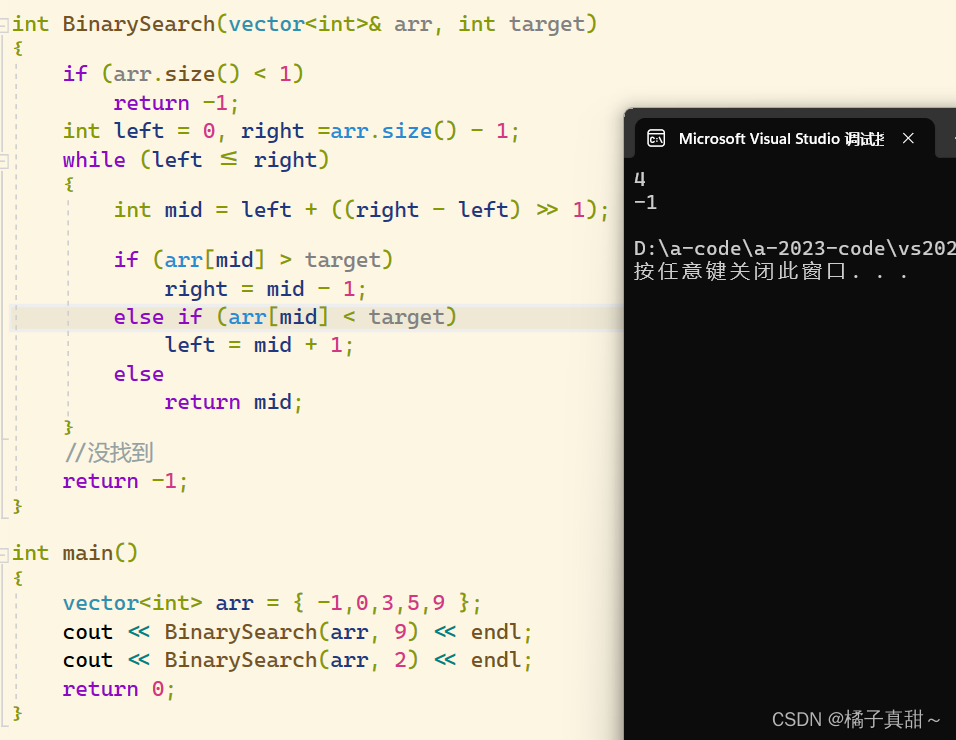
6.Leetcode相關練習題

704. 二分查找 - 力扣（LeetCode）

35. 搜索插入位置 - 力扣（LeetCode）

367. 有效的完全平方數 - 力扣（LeetCode）

69. x 的平方根 - 力扣（LeetCode）

34. 在排序數組中查找元素的第一個和最后一個位置 - 力扣（LeetCode）

下面這道題思想類似于二分查找，是高頻面試題之一

240. 搜索二維矩陣 II - 力扣（LeetCode）