?491. 非遞減子序列

491. 非遞減子序列https://leetcode.cn/problems/non-decreasing-subsequences/

題目描述：

給你一個整數數組?nums?，找出并返回所有該數組中不同的遞增子序列，遞增子序列中?至少有兩個元素?。你可以按?任意順序?返回答案。

數組中可能含有重復元素，如出現兩個整數相等，也可以視作遞增序列的一種特殊情況。

示例 1：

輸入：nums = [4,6,7,7]
輸出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

輸入：nums = [4,4,3,2,1]
輸出：[[4,4]]

• -100 <= nums[i] <= 100

思路分析：

注意，本題不能像算法練習第24天|78.子集、 90.子集II-CSDN博客中的90.子集II那樣對元素組進行排序已達到元素子序列去重的目的，可以看上面的示例2，如果我們按照90題那樣的做法對原數組進行排列的話【1，2，3，4，4】，就會得出不止一個非遞減子序列，這顯然與題目輸出的【4，4】不符合。所以我們不能對原序列進行排序。

本題給出的示例，還是一個有序數組 [4, 6, 7, 7]，這更容易誤導大家按照排序的思路去做了。

為了有鮮明的對比，我用[4, 7, 6, 7]這個數組來舉例，抽象為樹形結構如圖：

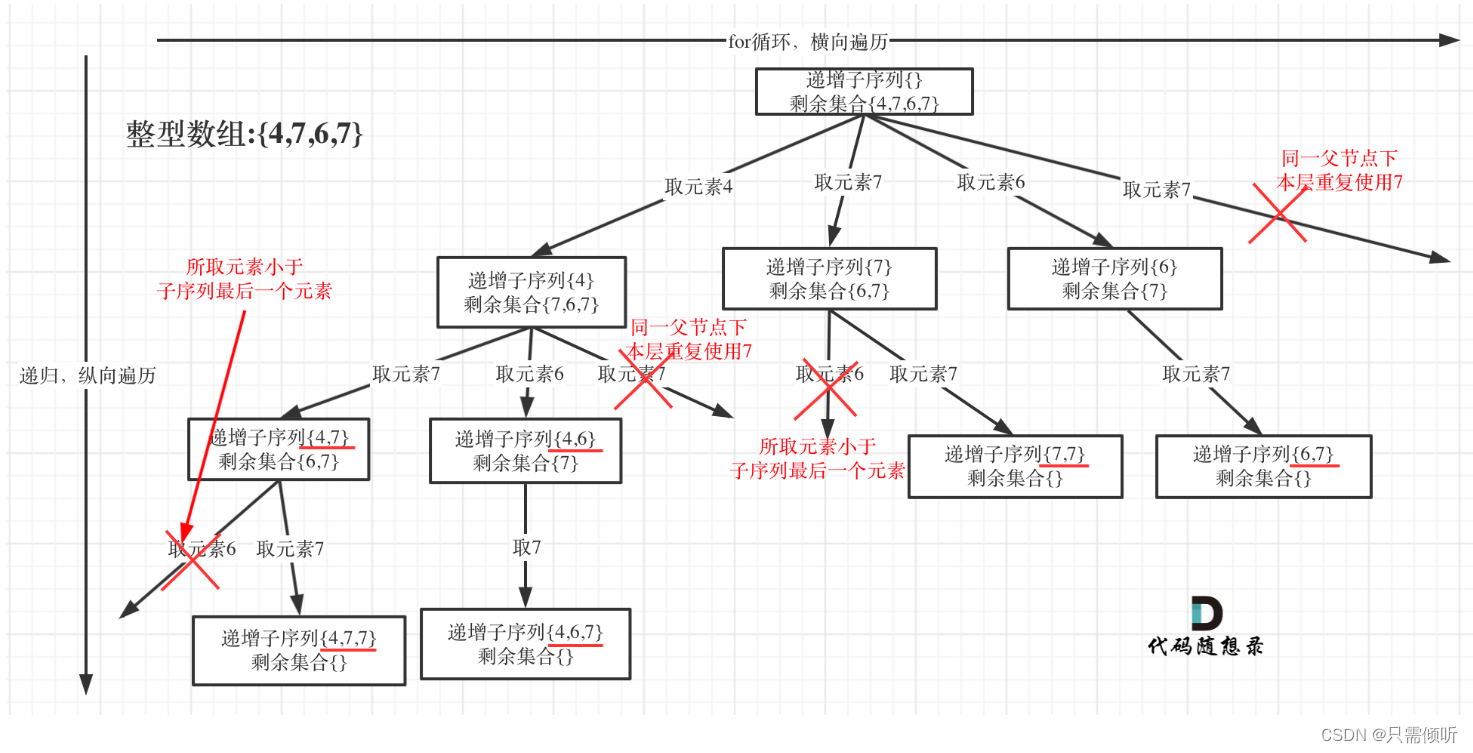
按照正常的前后順序進行搜索，會發現兩種情況下元素是不能記錄的：

（1）如果當前元素比剛剛記錄的元素小，那么當前元素就不能往path中添加，因為此時不符合非遞減的性質。

（2）同一父節點下的那一層遍歷，如果元素之前用過，那么也不能向path中添加。

上面兩種情況任意一種發生，path就不能記錄當前元素。所以這兩種情況對應代碼的邏輯關系是或||。

下面開始日常的回溯三部曲：

第一步：確認回溯函數的參數與返回值。由于需要在一個集合里面取序列，所以要用到startIndex.

 vector<int> path;vector<vector<int>> result;void backTracking(vector<int> & nums, int startIndex){}

第二步：確認回溯終止條件。當startIndex達到nums.size()之后就遍歷完了，return。

    vector<int> path;vector<vector<int>> result;void backTracking(vector<int> & nums, int startIndex){  if(startIndex == nums.size()){return;}

第三步：確認單層遍歷邏輯。此時就要考慮到我們當前的元素nums[i]是否是上面所述的兩種不能記錄的情況了。條件（1）如果當前元素比剛剛記錄的元素小，用(!path.empty() && nums[i] < path.back())表示；條件（2）同一父節點下該元素（數值）之前用過，用used_numbers[nums[i]+100] == 1表示。

因為題目提示了nums所有元素-100 <= nums[i] <= 100，所以我們使用一個used_numbers數組來記錄元素是否用過。由于數組的下標是從0開始算的，所以我們將nums[i]+100，將元素的范圍【-100，100】線性拉伸到【0，200】，總共201個數。例如，當前元素為-100時，它存在數組的開始處，當元素為-99時，它存在數組的下標1處，依次類推。使用了該元素，則對應元素置1。另外也可以用set來記錄用過的數據。

        int used_numbers[201] = {0};  //記錄統一父節點下哪些數字是用過的for(int i = startIndex; i < nums.size(); i++){if((!path.empty() && nums[i] < path.back())|| used_numbers[nums[i]+100] == 1)continue;//不滿足if條件則表示該節點可以記錄，那么記錄當前節點path.push_back(nums[i]);//判斷path長度是否大于等于2，如果是，則reslut記錄if(path.size() > 1){result.push_back(path);}//-100到100映射到0-201used_numbers[nums[i]+100] = 1;  //用過該數字，標志為置1//因為子序列最少要有兩個元素，所以我們平常的result.push_back(path)就不能直接寫了//result.push_back(path);backTracking(nums, i+1);path.pop_back();}

整體代碼如下：

class Solution {
public:vector<int> path;vector<vector<int>> result;void backTracking(vector<int> & nums, int startIndex){if(startIndex == nums.size()){return ;}int used_numbers[201] = {0};  //記錄統一父節點下哪些數字是用過的for(int i = startIndex; i < nums.size(); i++){if((!path.empty() && nums[i] < path.back())|| used_numbers[nums[i]+100] == 1)continue;//記錄當前節點path.push_back(nums[i]);if(path.size() > 1){result.push_back(path);}//-100到100映射到0-201used_numbers[nums[i]+100] = 1;  //用過該數字，標志為置1//因為子序列最少要有兩個元素，所以我們平常的result.push_back(path)就不能直接寫了//result.push_back(path);backTracking(nums, i+1);path.pop_back();}}vector<vector<int>> findSubsequences(vector<int>& nums) {backTracking(nums, 0);return result;}
};

下面是使用unordered_set<int>來記錄重復元素的寫法：

class Solution {
public:vector<int> path;vector<vector<int>> result;void backTracking(vector<int> & nums, int startIndex){if(startIndex == nums.size()){return ;}unordered_set<int> used_numbers;  //記錄統一父節點下哪些數字是用過的for(int i = startIndex; i < nums.size(); i++){if((!path.empty() && nums[i] < path.back())|| used_numbers.find(nums[i]) != used_numbers.end())continue;//記錄當前節點path.push_back(nums[i]);if(path.size() > 1){result.push_back(path);}//-100到100映射到0-201used_numbers.insert(nums[i]);  //用過該數字，標志為置1//因為子序列最少要有兩個元素，所以我們平常的result.push_back(path)就不能直接寫了//result.push_back(path);backTracking(nums, i+1);path.pop_back();}}vector<vector<int>> findSubsequences(vector<int>& nums) {backTracking(nums, 0);return result;}
};

注意：不管是使用數組還是set來存放使用過的數字，它們都只存在與當前遞歸層，即下一層的遞歸中數組和set都會重新創建并初始化，然后for循環在同一層中遍歷，這就保證了同一父節點下可以查找元素使用已經用過。

另外，在使用set時，程序運行的時候對unordered_set 頻繁的insert，unordered_set需要做哈希映射（也就是把key通過hash function映射為唯一的哈希值）相對費時間，而且每次重新定義set，insert的時候其底層的符號表也要做相應的擴充，也是費事的。使用數組程序還快一些。算法訓練第5天|哈希表理論基礎 242.有效的字母異位詞 349. 兩個數組的交集 202. 快樂數 1. 兩數之和-CSDN博客

在上面這篇博文349題中，提到了數組和set作為哈西表時各自的應用場景：

而且如果哈希值比較少、特別分散、跨度非常大，使用數組就造成空間的極大浪費，優先使用set和map。數組，set，map都可以做哈希表，而且數組干的活，map和set都能干，但如果數值范圍小的話能用數組盡量用數組。