動態規劃類問題
- 從已知子問題的解,推導出當前問題的解 推導過程可以表達為一個數學公式
- 用一維或二維數組來保存之前的計算結果(可以進一步降維優化)
????????將當前問題 分解成子問題 ,找出遞歸公式,分階段進行求解 求解過程中緩存子問題的解,避免重復計算。
以一個簡單例子Fibonacci數列為例,求Fibonacci數列第 n 項的
從第二項開始,每一項的值都等于前兩項的值之和
0 1 1 2 3 5 8
dp[i] = dp[i-1] + dp[i-2]
思路:
? ? ? ? 1.若求第 0 項或第 1 項的值,直接返回對應的值 0 或 1
? ? ? ? 2.創建一個一維數組緩存第n項數值之前的求解結果,并初始化第一項和第二項的值
? ? ? ? 3.使用循環計算處每一項的值,直到第 n 項,最后返回一維數組的第n項值即可
代碼:
public static int fibonacci(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;}int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}測試:
public static void main(String[] args) {// 0 1 1 2 3 5 8System.out.println(fibonacciDown(13)); //求第 7 項值
}降維優化:對于每個子問題只需要三個值參與,何不用三個變量代替一維數組進行優化:
/*** 求 Fibonacci 的第 n 項 (降維)** @param n 第幾項* @return*/public static int fibonacciDown(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;}int a = 0, b = 1;for (int i = 2; i <= n; i++) {int c = a + b; //記錄第i項的值//更新值 a = b;b = c;}return b;}Leecode62. 不同路徑?題
從start走到finish有多少種走法(只能向右或向下走)
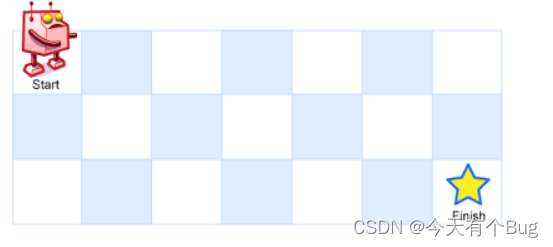
?將每個格子的走法都記錄出來,標識數字為 start 到該格子上的有多少走法,,找出規律

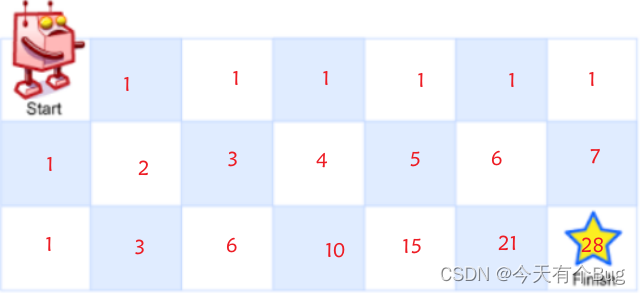
可看出規律為:dp[i][j] = dp[i][j - 1] + dp[i -1][j],并且第一行和第一列的值都為1,即走法只有一種
思路:
? ? ? ? 1.以一個二維數組緩存每個格子的走法數
? ? ? ? 2.遍歷每行每列,求出每個格子的走法數
? ? ? ? 3.最后返回第m行第n列的值,即為最終結果
代碼:
/*** 求到第m行n列有多少種走法,只能向右和向下** @param m* @param n* @return*/public static int uniquePaths2(int m, int n) {int[][] dp = new int[m][n];//初始化第一行和第一列的值為 1(其走法只有一種)for (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int i = 0; i < n; i++) {dp[0][i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}print(dp);return dp[m - 1][n - 1];}降維優化:
每次計算當前格子的走法數時,只需要上一個格子和左邊格子的走法之和,何不使用一維數組,上一個格子的走法即為當前格子的做法,將dp[i][j] = dp[i][j - 1] + dp[i -1][j]改為dp[j] = dp[j] + dp[j - 1],實現降維優化的目的,以第二行到第三行為例:

代碼:
/*** 求到第m行n列有多少種走法,只能向右和向下 (降維,二維 變 一維)** @param m* @param n* @return*/public static int uniquePaths(int m, int n) {int[] dp = new int[n];//初始化第一行和第一列的值為 1(其走法只有一種)Arrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] = dp[j] + dp[j - 1]; //自己加上 上一列的}}
// System.out.println(Arrays.toString(dp));return dp[n - 1];}2. 01背包問題 - AcWing題庫
從N個物體中選擇物體放入體積為V的背包中,使得價值最大,每種物品只能選擇一次
以一下測試示例:
4 5 //物體數量為 4,背包體積為 5
1 2 //第一個物體的體積 1 和價值 2
2 4
3 4
4 5以一個二維數組緩存第一行只有物品A的選擇,第二行只有物體A、B時的選擇等..,
ABCD分別表示四個物體
二維數組 dp 中:
第一行中選擇物體A,體積為1,在體積為0時不能放下為0,其它都能放下A
第二行中選擇物體B,體積為2,在背包體積為0、1時不能放下,將上一行數據復制下來,背包體積為2時能放下,價值為2比上一行的A更大,為3、4、5時可以放下B此外還能放下一個物體A
第三行中選擇物體C,體積為3,在背包體積為0、1、2時不能放下,將上一行數據復制下來,在背包體積 為3是雖然能放下C,但是上一行的BA價值是6,比C的價值大,所以直接復制下來,在體積為5時,當前背包除了能放下BA外還能放下一個C
第四行選擇物體D,體積為4,在背包體積為0、1、2、3時不能放下,將上一行數據復制下來,在背包體積 為4是雖然能放下D,但是上一行的BA價值是6,比D的價值大,所以直接復制下來,在體積為5時同理
編號 體積(g) 價值(元) 物品名1 1 2 A2 2 4 B3 3 4 C4 4 5 D
二維數組 dp :0 1 2 3 4 5 --> 背包體積0 0 A A A A A A1 0 A B BA BA BA B2 0 A B BA BA BAC C3 0 A B BA BA BAC D0, 2, 2, 2, 2, 20, 2, 4, 6, 6, 60, 2, 4, 6, 6, 80, 2, 4, 6, 6, 8結果:8 (BAC)總結一個規律:
1.裝得下 —— 當前物品價值比上一行價值更大時,選擇當前物品,再加上總體積 - 當前物品體積得到的體積值列中最大價值得物品,加到當前處dp[i][j] = Math.max(dp[i-1][j],currItemValue + dp[i-1][jTotal - currItem.weight]) 比如dp數組中:dp[1][3] = Max(dp[0][3],B + dp[0][3-2]) = BA 2.裝不下,將上一行物品復制下來dp[i][j] = dp[i-1][j]
代碼二維:
import java.util.Scanner;/*** 0 - 1背包問題*/
public class Main {public static void main(String[] args) {
/*編號 體積(g) 價值(元) 物品名1 1 2 A2 2 4 B3 3 4 C4 4 5 D0 1 2 3 4 5 --> 體積0 0 A A A A A A1 0 A B BA BA BA B2 0 A B BA BA BAC C3 0 A B BA BA BAC D0, 2, 2, 2, 2, 20, 2, 4, 6, 6, 60, 2, 4, 6, 6, 80, 2, 4, 6, 6, 8結果:8 (BAC)1.裝得下 —— 當前物品價值比上一行價值更大時,選擇當前物品,再加上總體積 - 當前物品體積量得到得體積列中最大價值得物品,加到當前處dp[i][j] = Max(dp[i-1][j],currItemValue + dp[i-1][jTotal - currItem.weight]) 比如:dp[3][8] = Max(dp[2][8],D + dp[2][8-1]) = DA2.裝不下,將上一行物品復制下來dp[i][j] = dp[i-1][j]*/Scanner sc = new Scanner(System.in);int N = sc.nextInt(); //物品數量int V = sc.nextInt(); //背包容積int[] vArr = new int[N]; //N個物品的體積int[] pArr = new int[N]; //N個物品的價值for (int i = 0; i < N; i++) {vArr[i] = sc.nextInt();pArr[i] = sc.nextInt();}System.out.println(knapsackProblem01(V, vArr, pArr, N));}public static int knapsackProblem01(int V, int[] vArr, int[] pArr, int N) {int[][] dp = new int[N][V + 1];for (int j = 0; j < V + 1; j++) {if (vArr[0] <= j) { //裝得下dp[0][j] = pArr[0];}}for (int i = 1; i < N; i++) {for (int j = 0; j < V+1; j++) {int x = dp[i - 1][j]; //上一行的價值if (vArr[i] <= j) { //裝得下// 當前物品價值 剩余物品價值dp[i][j] = Math.max(x, pArr[i] + dp[i-1][j - vArr[i]]);} else { //裝不下dp[i][j] = x;}}}return dp[N - 1][V];}}
?代碼(降維成一維數組):
public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt(); //物品數量int V = sc.nextInt(); //背包容積int[] vArr = new int[N]; //N個物品的體積int[] pArr = new int[N]; //N個物品的價值for (int i = 0; i < N; i++) {vArr[i] = sc.nextInt();pArr[i] = sc.nextInt();}int[] dp = new int[V + 1];for (int j = 0; j < V + 1; j++) {if (vArr[0] <= j) { //裝得下dp[j] = pArr[0];} else { //裝不下dp[j] = 0;}}//System.out.println(Arrays.toString(dp));for (int i = 1; i < N; i++){for (int j = V; j > 0; j--) {if (vArr[i] <= j) { //裝得下// pArr[i]當前物品價值 dp[j - vArr[i]]剩余空間在上次中(避免同一物品重復使用)能裝的最大值dp[j] = Math.max(dp[j], pArr[i] + dp[j - vArr[i]]);}}//System.out.println(Arrays.toString(dp));}System.out.println(dp[V]);}
3. 完全背包問題 - AcWing題庫
與01背包問題的區別:
dp[i][j] = Math.max(x, pArr[i] + dp[i][j - vArr[i]]); //完全背包中物品數量無限,從本次物品中找,同一物品可重復使用
dp[i][j] = Math.max(x, pArr[i] + dp[i-1][j - vArr[i]]); //01背包中物品數量只有一個,從上次物品中找,同一物品只能用一次
代碼(二維):
import java.util.Scanner;/*** 完全背包問題*/
public class Main {public static void main(String[] args) {
/*編號 體積(g) 價值(元) 物品名1 1 2 A2 2 4 B3 3 4 C4 4 5 D完全背包:0 1 2 3 4 5 --> 體積0 0 A AA AAA AAAA AAAAA A1 0 A B BA BB BBA B2 0 A B BA BB BBA C3 0 A B BA BB BBA D0 2 4 6 8 10 A0 2 4 6 8 10 B0 2 4 6 8 10 C0 2 4 6 8 10 D結果:10 (BAC)1.裝得下 —— 當前物品價值比上一行價值更大時,選擇當前物品,再加上(總體積 - 當前物品體積)得到的體積列中最大價值得物品,加到當前處dp[i][j] = Max(dp[i-1][j],currItemValue + dp[i-1][jTotal - currItem.weight]) 比如:dp[3][8] = Max(dp[2][8],D + dp[2][8-1]) = DA2.裝不下,將上一行物品復制下來dp[i][j] = dp[i-1][j]*/Scanner sc = new Scanner(System.in);int N = sc.nextInt(); //物品數量int V = sc.nextInt(); //背包容積int[] vArr = new int[N]; //N個物品的體積int[] pArr = new int[N]; //N個物品的價值for (int i = 0; i < N; i++) {vArr[i] = sc.nextInt();pArr[i] = sc.nextInt();}System.out.println(knapsackProblemComplete(V, vArr, pArr, N));}public static int knapsackProblemComplete(int V, int[] vArr, int[] pArr, int N) {int[][] dp = new int[N][V + 1];for (int j = 0; j < V + 1; j++) {if (vArr[0] <= j) { //裝得下dp[0][j] = pArr[0] + dp[0][j - vArr[0]];}}for (int i = 1; i < N; i++) {for (int j = 0; j < V + 1; j++) {int x = dp[i - 1][j]; //上一行的價值if (vArr[i] <= j) { //裝得下// 當前物品價值 剩余體積的物品價值(從本次中找)dp[i][j] = Math.max(x, pArr[i] + dp[i][j - vArr[i]]);} else { //裝不下dp[i][j] = x;}}}return dp[N - 1][V];}
}
降維:
import java.util.Scanner;/*** 完全背包問題*/
public class Main {public static void main(String[] args) {
/*1. n個物品都是固體,有重量和價值2. 現在你要取走不超過 10克 的物品3. 每件物品只能使用一次編號 體積(g) 價值(元) 物品名1 1 2 A2 2 4 B3 3 4 C4 4 5 D完全背包:0 1 2 3 4 5 --> 體積0 0 A AA AAA AAAA AAAAA A1 0 A B BA BB BBA B2 0 A B BA BB BBA C3 0 A B BA BB BBA D0 2 4 6 8 10 A0 2 4 6 8 10 B0 2 4 6 8 10 C0 2 4 6 8 10 D結果:10 (BAC)1.裝得下 —— 當前物品價值比上一行價值更大時,選擇當前物品,再加上總重量 - 當前物品重量得到得重量列中最大價值得物品,加到當前處dp[i][j] = Max(dp[i-1][j],currItemValue + dp[i-1][jTotal - currItem.weight]) 比如:dp[3][8] = Max(dp[2][8],D + dp[2][8-1]) = DA2.裝不下,將上一行物品復制下來dp[i][j] = dp[i-1][j]
4 5
1 2
2 4
3 4
4 5*/Scanner sc = new Scanner(System.in);int N = sc.nextInt(); //物品數量int V = sc.nextInt(); //背包容積int[] vArr = new int[N]; //N個物品的體積int[] pArr = new int[N]; //N個物品的價值for (int i = 0; i < N; i++) {vArr[i] = sc.nextInt();pArr[i] = sc.nextInt();}System.out.println(knapsackProblemComplete2(V, vArr, pArr, N));}/*** 取total重量的物品 并且 價值最大(降維)** @return 最大價值*/public static int knapsackProblemComplete2(int V, int[] vArr, int[] pArr, int N) {int[] dp = new int[V + 1];for (int j = 0; j < V + 1; j++) {if (vArr[0] <= j) { //裝得下dp[j] = pArr[0] + dp[j - vArr[0]];}}for (int i = 1; i < N; i++) {for (int j = 0; j < V + 1; j++) {int x = dp[j]; //上一行的價值if (vArr[i] <= j) { //裝得下// 當前物品價值 剩余物品價值dp[j] = Math.max(x, pArr[i] + dp[j - vArr[i]]);} else { //裝不下dp[j] = x;}}
// System.out.println(Arrays.toString(dp));}return dp[V];}
}


)




)











