C++|set、map模擬實現＜——紅黑樹

目錄

一、紅黑樹的迭代器

1.1紅黑樹迭代器框架

1.2operator*() && operator->()

1.3operator++()

1.4operator--()

1.5operator==()? && operator!=()?

1.6begin() && end()

二、如何用紅黑樹搭配map和set(仿函數)

?三、紅黑樹封裝map和set(簡易版)

3.1紅黑樹的構造(RBTree.h)?

3.2map的模擬實現(MyMap.h)

3.3set的模擬實現(MySet.h)

3.4測試(test.cpp)

?一、紅黑樹的迭代器

前一篇章，有了紅黑樹的了解，但那只實現了紅黑樹的插入部分，那么現在要用紅黑樹封裝set、map容器，那有一個功能，就必須得實現，即迭代器，對于紅黑樹的迭代器該如何實現呢？參考前面篇章，list容器的迭代器的實現，同樣的，紅黑樹將迭代器要實現的功能封裝成了一個類，那么接下來進行一步步實現。

1.1紅黑樹迭代器框架

由于迭代器的遍歷，實際就是遍歷節點，在實現具體步驟之前，先帶上節點，再把迭代器的框架搭好。?

	enum Color//對于紅黑節點，用枚舉結構來表示{RED,BLACK};template<class T>struct RBTreeNode{RBTreeNode(const T& data, Color color = RED):_left(nullptr),_right(nullptr),_parent(nullptr),_data(data),_color(color){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _color;//默認給紅色才符合規則，若默認給黑色的話，則插入的每個節點都是黑色節點，//那么就不能保證每條路徑的黑色節點相同，違反了第4條性質。而給紅色，就可以根據規則調整。};template<class T, class Ref, class Ptr>struct RBTreeIterator{typedef RBTreeNode<T> Node;typedef Node* PNode;typedef RBTreeIterator<T, Ref, Ptr> Self;PNode _node;RBTreeIterator(const PNode node):_node(node){}//.....};

1.2operator*() && operator->()

        T& operator*(){return _node->_data;//訪問節點數據}T* operator->(){return &(operator*());//operator*() == _node->_data}

1.3operator++()

?對紅黑樹的遍歷是一個中序遍歷，遍歷完后，得到的是一個有序序列。每++一次，跳到的位置是中序序列中的下一個位置。我們知道中序的訪問順序是，左根右，那么如何在樹上進行操作而達到中序遍歷呢？

大致可以分為兩步：

1.當左子樹與根訪問完，要符合中序，得去右子樹進行訪問，同理右子樹得滿足中序遍歷，首先就得找到右子樹的最小節點，即最左節點。

抽象示意圖：

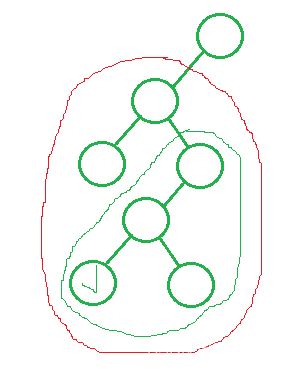
2.當左子樹未訪問完，++時，就指向父節點，

抽象示意圖：

或者當右子樹訪問完了，則說明一顆節點的整個左子樹訪問完了。那么++就是要找到這個節點

抽象示意圖：?

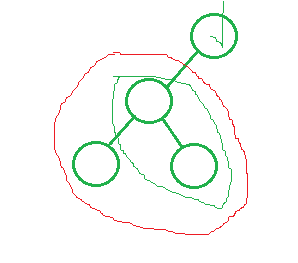
        Self& operator++(){if (_node->_right)//左子樹訪問完，去訪問右子樹{_node = _node->_right;while (_node && _node->_left){_node = _node->_left;}}else//左子樹未訪問完，或者右子樹訪問完{PNode cur = _node;PNode parent = cur->_parent;while (parent && cur != parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

1.4operator--()

那么，對于--操作，它與++操作是反過來的，是從大到小的一個遍歷。

1.?當右子樹與根訪問完，要符合大到小的遍歷，得去左子樹進行訪問，同理左子樹得滿足大到小的遍歷，首先就得找到左子樹的最大節點，即最右節點。

2.當右子樹未訪問完，或者左子樹已訪問完

Self& operator--(){PNode cur = _node;PNode parent = cur->_parent;if (_node->_left)//右子樹訪問完，去左子樹訪問{_node = _node->_left;while (_node->_right){_node = _node->_right;}}else//右子樹未訪問完，或者左子樹訪問完{PNode cur = _node;PNode parent = cur->_parent;if (parent && cur != parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

1.5operator==()? && operator!=()?

        bool operator==(const Self& x) const{return _node == x._node;}bool operator!=(const Self& x) const{return _node != x._node;}

?1.6begin() && end()

搭建好了迭代器，那么如何在紅黑樹中定義begin和end()，按正常的理解， begin返回指向中序序列第一個元素的迭代器，end()返回指向中序序列最后一個元素下一個位置的迭代器。

        iterator begin(){PNode cur = _Root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){		return iterator(nullptr);}

begin的返回值是沒有問題，但是end就不一樣了，end指向的是nullptr，當要實行end()--操作時，迭代器就會指向最后一個元素的位置，但是end已經指向空了呀，而--的操作是通過更改指針指向，那么更改end指向，就是要對空指針進行解引用，就會報錯。

那么正確的做法就是將end()放在頭結點的位置。即構建一個頭結點用來存放begin和end，該頭結點與樹的頭結點互相指向，對于這種做法，這里并不會去實現，還是按照原來的做法進行實現。

二、如何用紅黑樹搭配map和set(仿函數)

我們可以用兩顆紅黑樹分別封裝一份map和一份set，但是這樣做的效果就帶來了代碼冗余。為了減少代碼冗余，模擬跟庫保持用一顆紅黑樹封裝map和set，但是該如何做到套用一顆樹呢，我們來進一步分析。

?首先對于map而言，其存放的節點值是pair，而對于set存放的是key，這對于紅黑樹節點的實現到是沒啥問題，但是對于紅黑樹內部的構造，是需要查詢插入的位置，就需要進行比較，若將比較實現成key的比較，那么對于pair類型又該如何比較，雖然知道比較的也是pair中的key，但是如何做到既滿足set中的key類型比較，又滿足pair類型中的key比較，總不能干兩份代碼吧。這個時候，我們的仿函數又派上用場了，對于set和map中都構造一個仿函數，分別表示取到set的key，和map中pair中的key，那么紅黑樹中的比較，就可以換成仿函數的比較，當往set中插入元素進行比較，調用的就是set的仿函數，當往map中插入元素進行比較，調用的就是map的仿函數從而達到回調。用一張圖來進行表示，如圖：

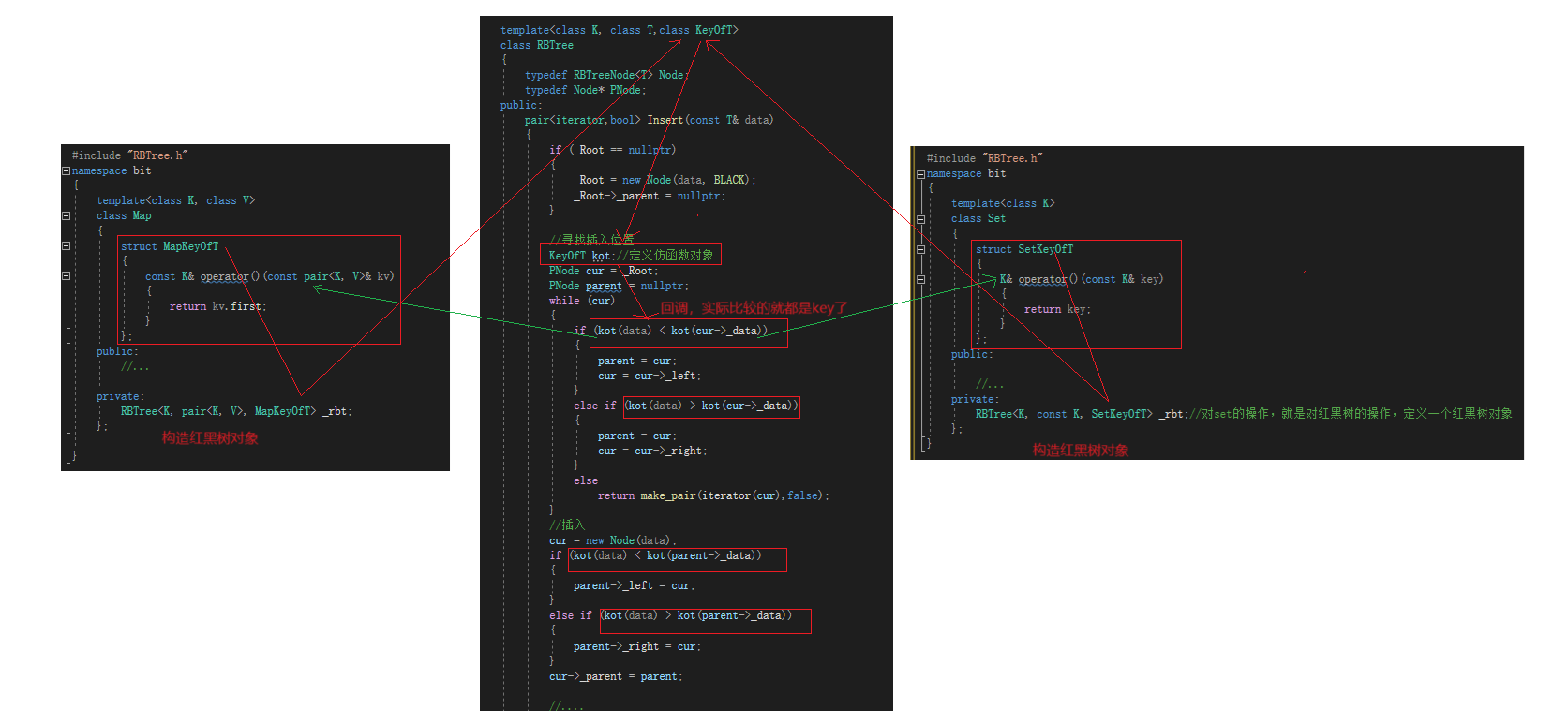
?三、紅黑樹封裝map和set(簡易版)

3.1紅黑樹的構造(RBTree.h)?

#pragma once
#include <iostream>
#include <assert.h>
using namespace std;namespace bit
{enum Color//對于紅黑節點，用枚舉結構來表示{RED,BLACK};template<class T>struct RBTreeNode{RBTreeNode(const T& data, Color color = RED):_left(nullptr),_right(nullptr),_parent(nullptr),_data(data),_color(color){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _color;//默認給紅色才符合規則，若默認給黑色的話，則插入的每個節點都是黑色節點，//那么就不能保證每條路徑的黑色節點相同，違反了第4條性質。而給紅色，就可以根據規則調整。};template<class T, class Ref, class Ptr>struct RBTreeIterator{typedef RBTreeNode<T> Node;typedef Node* PNode;typedef RBTreeIterator<T,Ref,Ptr> Self;PNode _node;RBTreeIterator(const PNode node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &(operator*());}Self& operator++(){if (_node->_right)//左子樹訪問完，去訪問右子樹{_node = _node->_right;while (_node && _node->_left){_node = _node->_left;}}else//左子樹未訪問完，或者右子樹訪問完{PNode cur = _node;PNode parent = cur->_parent;while (parent && cur != parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator--(){PNode cur = _node;PNode parent = cur->_parent;if (_node->_left)//右子樹訪問完，去左子樹訪問{_node = _node->_left;while (_node->_right){_node = _node->_right;}}else//右子樹未訪問完，或者左子樹訪問完{PNode cur = _node;PNode parent = cur->_parent;if (parent && cur != parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator==(const Self& x) const{return _node == x._node;}bool operator!=(const Self& x) const{return _node != x._node;}};template<class K, class T,class KeyOfT>class RBTree{typedef RBTreeNode<T> Node;typedef Node* PNode;public:typedef RBTreeIterator<T,T&,T*> iterator;typedef RBTreeIterator<const T, const T&, const T*> const_iterator;RBTree():_Root(nullptr){}iterator begin(){PNode cur = _Root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){		return iterator(nullptr);}const_iterator begin() const{PNode cur = _Root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}const_iterator end() const{return iterator(nullptr);}pair<iterator,bool> Insert(const T& data){if (_Root == nullptr){_Root = new Node(data, BLACK);_Root->_parent = nullptr;return make_pair(iterator(_Root), true);}//尋找插入位置KeyOfT kot;//定義仿函數對象PNode cur = _Root;PNode parent = nullptr;while (cur){if (kot(data) < kot(cur->_data)){parent = cur;cur = cur->_left;}else if (kot(data) > kot(cur->_data)){parent = cur;cur = cur->_right;}elsereturn make_pair(iterator(cur),false);}//插入cur = new Node(data);if (kot(data) < kot(parent->_data)){parent->_left = cur;}else if (kot(data) > kot(parent->_data)){parent->_right = cur;}cur->_parent = parent;//調整while (parent && parent->_color == RED)//只要停留在情況一就繼續判斷{PNode grandparent = parent->_parent;PNode uncle = nullptr;//先定好uncle的位置，不管uncle是否存在if (parent == grandparent->_left){uncle = grandparent->_right;}else{uncle = grandparent->_left;}if (uncle && uncle->_color == RED)//p為紅、u存在且為紅{//    g//  p   u// curparent->_color = BLACK;uncle->_color = BLACK;grandparent->_color = RED;//根節點，更新結束if (grandparent == _Root){grandparent->_color = BLACK;break;}//往上更新cur = grandparent;parent = cur->_parent;}else if (cur == parent->_left && parent == grandparent->_left )//cur為p的左孩子，p為g的左孩子，p為紅{//     g//  p     u//curRotateR(grandparent);parent->_color = BLACK;grandparent->_color = RED;break;}else if (cur == parent->_right &&  parent == grandparent->_right )//cur為p的右孩子，p為g的右孩子，p為紅{//     g// u      p//          curRotateL(grandparent);parent->_color = BLACK;grandparent->_color = RED;break;}else if (cur == parent->_right && parent == grandparent->_left )//p為g的左孩子，cur為p的右孩子，p為紅{//   g//p     u//  curRotateL(parent);RotateR(grandparent);cur->_color = BLACK;grandparent->_color = RED;break;}else if (cur == parent->_left && parent == grandparent->_right)//p為g的右孩子，cur為p的左孩子，p為紅{//   g//u     p//   curRotateR(parent);RotateL(grandparent);cur->_color = BLACK;grandparent->_color = RED;break;}else{assert(false);}}return make_pair(iterator(cur),true);}iterator Find(const T& data){if (_Root == nullptr)return end();PNode cur = _Root;KeyOfT kot;while (cur){if (kot(data) < kot(cur->_data)){cur = cur->_right;}else if (kot(data) > kot(cur->_data)){cur = cur->_left;}else return iterator(cur);}return end();}size_t _Size(PNode Root,int k){if (Root == nullptr)return 0;int leftsize = _Size(Root->_left, k);int rightsize = _Size(Root->_right, k);return leftsize + rightsize + 1;}size_t Size() {int k = 0;return _Size(_Root, k);}bool Empty(){return _Root == nullptr;}void RotateL(PNode parent){PNode subR = parent->_right;PNode subRL = subR->_left;PNode pparent = parent->_parent;if (parent == _Root)//更新根節點{_Root = subR;subR->_parent = nullptr;}else{//更新parent的父節點指向if (parent == pparent->_left){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}//parent的右指針指向subRL,subRL的父節點指向parentparent->_right = subR->_left;if (subRL)//subR的左節點可能不存在subRL->_parent = parent;//subR的左指針指向parent,parent的父節點指向subRsubR->_left = parent;parent->_parent = subR;}//右單旋void RotateR(PNode parent){PNode subL = parent->_left;PNode subLR = subL->_right;PNode pparent = parent->_parent;if (_Root == parent){_Root = subL;subL->_parent = nullptr;}else{//更新parent的父節點指向if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}//parent的左指針指向subLR,subLR的父節點指向parentparent->_left = subLR;if (subLR)//subR的右節點可能不存在subLR->_parent = parent;//subL的右指針指向parent,parent的父節點指向subLsubL->_right = parent;parent->_parent = subL;}private:PNode _Root;};}

3.2map的模擬實現(MyMap.h)

#pragma once
#include "RBTree.h"
namespace bit
{template<class K,class V>class Map{struct MapKeyOfT{const K& operator()(const pair<K,V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _rbt.begin();}iterator end(){return _rbt.end();}const_iterator begin() const{return _rbt.begin();}const_iterator end() const{return _rbt.end();}pair<iterator,bool> insert(const pair<K,V>& kv){return _rbt.Insert(kv);}V& operator[](const K& data){pair<iterator, bool> p = _rbt.Insert(make_pair(data, V()));//插入失敗，說明data已經存在，返回指向data的迭代器return p.first->second;}iterator find(const K& data){return _rbt.Find(data);}size_t size(){return _rbt.Size();}bool empty(){return _rbt.Empty();}private:RBTree<K, pair<K,V>, MapKeyOfT> _rbt;};}

?3.3set的模擬實現(MySet.h)

#pragma once
#include "RBTree.h"
namespace bit
{template<class K>class Set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;//set的迭代器使用的就是紅黑樹的迭代器typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;//set的迭代器使用的就是紅黑樹的迭代器iterator begin()//獲取set的首元素位置的迭代器，即獲取紅黑樹的最小元素的迭代器{return _rbt.begin();}iterator end(){return _rbt.end();}const_iterator begin() const{return _rbt.begin();}const_iterator end() const{return _rbt.end();}pair<iterator,bool> insert(const K& key)//插入元素實際就是插入到紅黑樹節點中去{return _rbt.Insert(key);}iterator find(const K& data){return _rbt.Find(data);}size_t size(){return _rbt.Size();}bool empty(){return _rbt.Empty();}private:RBTree<K,const K,SetKeyOfT> _rbt;//對set的操作，就是對紅黑樹的操作，定義一個紅黑樹對象};
}

3.4測試(test.cpp)

#define _CRT_SECURE_NO_WARNINGS 1
#pragma warning(disable:6031)#include "MyMap.h"
#include "MySet.h"void TestMapRBTree()
{int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };bit::Map<int, int> t;for (auto e : a){t.insert(make_pair(e, e));}bit::Map<int, int>::iterator it = t.begin();while (it != t.end()){cout << it->first << ":" << it->second << endl;++it;}cout << endl;
}void TestSetRBTree()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };bit::Set<int> t;for (auto e : a){t.insert(e);}bit::Set<int>::iterator it = t.begin();while (it != t.end()){cout << *it << endl;++it;}cout << t.size() << endl;cout << boolalpha << t.empty() << endl;
}int main()
{TestMapRBTree();TestSetRBTree();return 0;
}

輸出結果：

以上實現的是一個紅黑樹簡易版，雖然功能并不齊全，但目標是為了進一步學習對紅黑樹、map和set的掌握理解。end~

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/20445.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/20445.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/20445.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

springboot + Vue前后端項目（第十三記）

springboot + Vue前后端項目（第十三記）

項目實戰第十三記 寫在前面1.建立角色表2. 后端代碼生成2.1 RoleController 3. 前端頁面的搭建3.1 Role.vue3.2 路由3.3 Aside.vue3.4 頁面效果 4.建立菜單表5.后端代碼編寫5.1 Menu5.2 MenuController 6.前端頁面的搭建6.1 Menu.vue6.2 路由6.3 Aside.vue6.4 頁面效果 總結寫在…
閱讀更多...
keepalived安裝文檔

keepalived安裝文檔

目錄 1、安裝環境 2、安裝keepalived 2.1 上傳keepalived安裝文件 2.2 解壓 2.3 安裝keepalived 2.4 加入開機啟動&#xff1a; 2.5 配置日志文件 2.6 打開防火墻的通訊地址 1、安裝環境 su - root yum -y install kernel-devel* yum -y install openssl-* yum -y …
閱讀更多...
vx小程序初學

vx小程序初學

小程序初學 在我還沒接觸到微信小程序之前&#xff0c;通常使用輪播要么手寫或使用swiper插件去實現&#xff0c;當我接觸到微信小程序之后&#xff0c;我看到了微信小程序的強大之處&#xff0c;讓我為大家介紹一下吧&#xff01; swiper與swiper-item一起使用可以做輪播圖 …
閱讀更多...
把自己的服務器添加到presearch節點

把自己的服務器添加到presearch節點

Presearch is a scam. Before, judging by the price of the token you should have been able to get between $150-$200 after 12-13 months of regular searches. "If you use this service for the next 11 years you will have earned $30!" Presearch大約需要…
閱讀更多...
Easy RoCE：在SONiC交換機上一鍵啟用無損以太網

Easy RoCE：在SONiC交換機上一鍵啟用無損以太網

RDMA&#xff08;遠程直接內存訪問&#xff09;技術是一種繞過 CPU 或操作系統&#xff0c;在計算機之間直接傳輸內存數據的技術。它釋放了內存帶寬和 CPU&#xff0c;使節點之間的通信具有更低的延遲和更高的吞吐量。目前&#xff0c;RDMA 技術已廣泛應用于高性能計算、人工智…
閱讀更多...
車流量監控系統

車流量監控系統

1.項目介紹 本文檔是對于“車流量檢測平臺”的應用技術進行匯總&#xff0c;適用于此系統所有開發&#xff0c;測試以及使用人員&#xff0c;其中包括設計背景&#xff0c;應用場景&#xff0c;系統架構&#xff0c;技術分析&#xff0c;系統調度&#xff0c;環境依賴&#xf…
閱讀更多...
MongoDB~存儲引擎了解

MongoDB~存儲引擎了解

存儲引擎 存儲引擎是一個數據庫的核心&#xff0c;主要負責內存、磁盤里數據的管理和維護。 MongoBD的優勢&#xff0c;在于其數據模型定義的靈活性、以及可拓展性。但不要忽略&#xff0c;其存儲引擎也是插件式的存在&#xff0c;支持不同類型的存儲引擎&#xff0c;使用不同…
閱讀更多...
導線防碰撞警示燈：高壓線路安全保障

導線防碰撞警示燈：高壓線路安全保障

導線防碰撞警示燈&#xff1a;高壓線路安全保障 在廣袤的大地上&#xff0c;高壓線路如同血脈般縱橫交錯&#xff0c;然而&#xff0c;在這看似平靜的電力輸送背后&#xff0c;卻隱藏著不容忽視的安全隱患。特別是在那些輸電線路跨越道路、施工等區域的路段&#xff0c;線下超…
閱讀更多...
頂點著色技術在AI去衣中的作用

頂點著色技術在AI去衣中的作用

在當今的數字時代&#xff0c;人工智能&#xff08;AI&#xff09;已經滲透到我們生活的方方面面&#xff0c;從智能家居到自動駕駛汽車&#xff0c;再到在線購物推薦。然而&#xff0c;AI的影響遠不止于此。近年來&#xff0c;AI在圖像處理和計算機視覺領域的應用取得了顯著進…
閱讀更多...
c++字符串相關接口

c++字符串相關接口

c字符串相關接口 1.str2wstr(str轉換wstr)2.wstr2str(str轉換wstr)3.Utf8ToAsi(Utf8轉換ANSI)4.AsiToUtf8(ANSI轉換Utf8)5.stringformatA/stringformatW(按照指定的格式格式化字符串)6.GetStringBetween(獲取cStart cEnd之間的字符串)7.Char2Int(char轉int)8.Str2Bin(字符串轉換…
閱讀更多...
視覺語言大模型llava學習

視覺語言大模型llava學習

1. 拉取 https://github.com/haotian-liu/LLaVA 視覺語言大模型是人工智能領域一種重要的多模態模型&#xff0c;它結合了計算機視覺&#xff08;CV&#xff09;和自然語言處理&#xff08;NLP&#xff09;的技術&#xff0c;使得模型能夠同時理解圖像和文本信息。這類模型在多…
閱讀更多...
hadoop部署

hadoop部署

需要3臺機子&#xff0c;Linux為centos7 分別設置靜態ip&#xff0c;設置主機名,配置主機名映射&#xff0c;配置ssh免密登入 hadoop1 192.168.1.7 hadoop2 192.168.1.8 hadoop3 192.168.1.9 vi /etc/sysconfig/network-scripts/ifcfg-ens33TYPE"Ethernet" PROX…
閱讀更多...
Kotlin 泛型

Kotlin 泛型

文章目錄 定義泛型屬性泛型函數泛型類或接口 where 聲明多個約束泛型具體化in、out 限制泛型輸入輸出 定義 有時候我們會有這樣的需求&#xff1a;一個類可以操作某一類型的對象&#xff0c;并且限定只有該類型的參數才能執行相關的操作。 如果我們直接指定該類型Int&#xff…
閱讀更多...
機器人抓取檢測（Robot Grasping Detection）

機器人抓取檢測（Robot Grasping Detection）

目錄 前言 一、物體檢測 二、抓取點生成 三、運動規劃 四、控制 五、總結 前言 機器人抓取檢測&#xff08;Robot Grasping Detection&#xff09;是指通過計算機視覺和機器學習技術&#xff0c;自動識別并確定機器人如何抓取物體的一種技術。這個過程涉及多個步驟和關鍵…
閱讀更多...
【Python系列】Python 中方法定義與方法調用詳解

【Python系列】Python 中方法定義與方法調用詳解

&#x1f49d;&#x1f49d;&#x1f49d;歡迎來到我的博客&#xff0c;很高興能夠在這里和您見面&#xff01;希望您在這里可以感受到一份輕松愉快的氛圍&#xff0c;不僅可以獲得有趣的內容和知識&#xff0c;也可以暢所欲言、分享您的想法和見解。 推薦:kwan 的首頁,持續學…
閱讀更多...
詳細介紹運算符重載函數，清晰明了

詳細介紹運算符重載函數，清晰明了

祝各位六一快樂~ 前言 1.為什么要進行運算符重載&#xff1f; C中預定義的運算符的操作對象只能是基本數據類型。但實際上&#xff0c;對于許多用戶自定義類型&#xff08;例如類&#xff09;&#xff0c;也需要類似的運算操作。這時就必須在C中重新定義這些運算符&#xff…
閱讀更多...
短信發送驗證碼及郵件發送驗證碼

短信發送驗證碼及郵件發送驗證碼

發送短信驗證碼 阿里云發送驗證碼 public Integer sendTelCode(String tel) {String url "https://dfsns.market.alicloudapi.com/data/send_sms";String appcode "a3198282fbdf443d97aa9f3cfbe1232e";int code RandomUtil.randomInt(1000,10000);emai…
閱讀更多...
【DSP】xDAIS算法標準

【DSP】xDAIS算法標準

1. 簡介 在安裝DSP開發支持包時&#xff0c;有名為 “xdais_7_21_01_07”文件夾。xDAIS全稱: TMS320 DSP Algorithm Standard(算法標準)。39條規則&#xff0c;15條指南。參考文檔。參考文章。 2. 三個層次 3.接口 XDAIS Digital Media。編解碼引擎。VISA&#xff08;Video&…
閱讀更多...
LeetCode前端刷題指南：探索四大領域，精通五大技能，掌握六大題型，運用七大策略

LeetCode前端刷題指南：探索四大領域，精通五大技能，掌握六大題型，運用七大策略

LeetCode前端刷題指南&#xff1a;探索四大領域&#xff0c;精通五大技能&#xff0c;掌握六大題型&#xff0c;運用七大策略 在前端開發的廣闊領域中&#xff0c;刷題是提高自身能力、深入理解算法和數據結構的重要途徑。LeetCode作為知名的在線刷題平臺&#xff0c;為前端開…
閱讀更多...
牛客小白月賽95VP

牛客小白月賽95VP

早上藍橋杯大寄&#xff0c;算是交了300元買了件T恤qaq 1.簽到&#xff1a;https://ac.nowcoder.com/acm/contest/83687/A 下面是AC代碼&#xff1a; #include<bits/stdc.h> using namespace std; int main() {int a,b;cin>>a>>b;if(ab) cout<<&quo…
閱讀更多...
最新文章

Copyright @ 2022~2023